| kategória | ||||||||||
|
|
||||||||||
|
|
||
Attól függöen, hogy az adatmodellben milyen logikai kapcsolatokat engednek meg az egyedhalmazok között és ezeket a kapcsolatokat hogyan kezelik, az adatbáziskezelö rendszereket három fö típusba sorolhatjuk:
- hierarchikus
- hálós
- relációs adatbáziskezelö rendszerek.
Az elsö adatbáziskezelö rendszerek nagyszámítógépeken jelentek meg. Ezek többsége a hierarchikus modell szerint épült fel. Ennek lényege, hogy az egyedhalmazok között csak hierarchikus kapcsolatot enged meg (1:N típusú kapcsolat). Ez az adatstruktúra egy fával ábrázolható. Például egy tantárgynyilvántartás esetén a tantárgyak rekordjai tartalmazzák a tantárgyakat jellemzö adatokat (tantárgy kódja, címe, óraszám, követelmény, stb.), a tanszékek rekordjai pedig a tanszékekre jellemzö adatokat (tanszék kódja, neve, vezetö neve, stb.). Egy tanszék több tantárgyat is meghirdethet, de egy tantárgyat csak egy tanszék hirdet meg, így a tantárgyak és a tanszékek között 1:N típusú kapcsolat van, vagyis hierarchikus kapcsolatban állnak egymással.

A tanszékrekord a szülö, vagy tulajdonos, a tantárgyrekordok pedig a gyerek, vagy tag rekordok.
A fastruktúra több szintü is lehet. Példánkban a tanszékek valamilyen szervezeti egységhez tartoznak, az egyes szervezeti egységek pedig valamilyen szervezeti egység-csoporthoz.

A legegyszerübb hierarchikus modellek csak egyfajta fastruktúrából állnak, míg bonyolultabb modellek esetén egy adatbázison belül többféle fastruktúra elöfordulhat.
A fastruktúra fizikai megvalósítása általában az adatrekordokban elhelyezett pointerek (mutatók) segítségével történik. Egy adatrekordban pointer mutat a szülö rekordra, valamint a gyerek rekordokra, vagy a testvérekre.
Az így kialakított hierarchikus struktúrában könnyen válaszolhatunk azokra a kérdésekre, amelyek illeszkednek az adatok logikai szerkezetéhez. Azon kérdések megválaszolása azonban, amelyeknél a visszakereséshez a logikai kapcsolatok nem használhatók, sok idöt vehetnek igénybe, hiszen ekkor soros keresést lehet csak alkalmazni.
A fenti példában arra a kérdésre, hogy mennyi
egy tanszék dolgozóinak átlagos életkora, könnyen megadható a válasz, hiszen a
szervezeti egység hierarchián, vagyis a fa ágain lefelé haladva el lehet jutni
a keresett tanszékhez, amelynek levelei a dolgozók adatait tartalmazzák.
Azonban csak hosszas kereséssel tudjuk megadni azokat, akik ebben az évben érik
el a nyugdíjkorhatárt, hiszen bármelyik szervezeti egységben lehet ilyen
dolgozó, ezért
A hierarchikus struktúra csak 1:N típusú kapcsolatok leírását teszi lehetövé, a valóságban az adatok között azonban gyakoribb az N:M kapcsolat. Ezt a kapcsolattípust próbálják leírni a hálós adatbázisok.
A hálós adatbázisokban az egyedtípusok között fennálló N:M kapcsolatot egy új csomóponttípus, a kapcsolatrekord segítségével kezeljük. A kapcsolatrekord általában azokat az adatokat tartalmazza, amelyek mindkét egyedtípustól függnek. Így az N:M típusú kapcsolatot lebontjuk 1:N és 1:M kapcsolatokra. Ezek a kapcsolatok már ábrázolhatók egyszerü hierarchiával. Tehát a hálós adatbázisok lényege, hogy kapcsolatrekordok segítségével olyan egyszerü hierarchiákat alakítunk ki, melynek elemei egyidejüleg több hierarchiában is részt vehetnek. Bonyolult adatösszefüggéseknél elöfordulhat, hogy többféle típusú kapcsolatrekordot kell létrehozni. Az adatmodell használata során semmilyen különbséget nem teszünk az adatrekordok és a kapcsolatrekordok között.
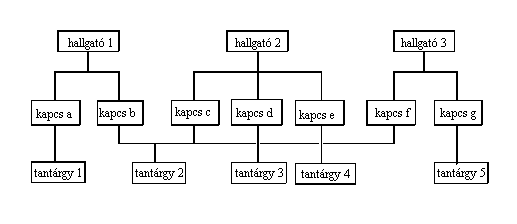
Például tekintsük a hallgatók és a tantárgyak nyilvántartását. A hallgatórekordok tartalmazzák a hallgatók adatait, a tantárgyrekordok pedig az egyes tantárgyakra vonatkozó adatokat. Egy hallgató egyszerre több tantárgyat hallgat, és egy tantárgyat több hallgató hallgat egy félévben. Így a hallgató és a tantárgy rekordok között N:M típusú kapcsolat van.

Vezessünk be kapcsolatrekordokat, amelyek a hallgató kódját és a tantárgy kódját tartalmazzák. Ekkor egy hallgatórekordhoz azok a kapcsolatrekordok tartoznak, amelyek az adott hallgató által felvett tantárgyak kódját tartalmazzák, az egyes tantárgyrekordokhoz pedig azok a kapcsolatrekordok, melyek azoknak a hallgatóknak a kódját tartalmazzák, akik a tárgyat hallgatják. Így mind a hallgató és a kapcsolat, mind a tantárgy és a kapcsolat rekordok között 1:N típusú kapcsolat áll fenn.

A kapcsolatrekordok mind a két hierarchiában szerepelnek. Ha összekapcsoljuk a két hierarchiát a kapcsolatrekordokon keresztül, akkor a kiinduló hálózatot kapjuk eredményül, vagyis a kiinduló N:M kapcsolatot kezelni lehet a két hierarchia segítségével.
A személyi számítógépeken föként a relációs adatbázisok használata terjedt el, ezért ezekkel részletesebben foglalkozunk.
A reláció fogalma
Legyen S1, S2,..., Sn adott halmazok. R az ezen n halmaz közötti reláció, ha olyan (s1,s2,...sn) n-esekböl áll, amelyek elsö eleme S1-böl, második eleme S2-böl, ...n. eleme Sn-böl származik. Az S1, S2,...,Sn halmazokat a reláció tartományainak nevezzük. A relációban szereplö tartományok száma (n) adja meg a reláció fokát.
Az adatmodellben az egyedeket tulajdonságokkal írjuk le. Ezeknek a tulajdonságoknak egy-egy halmaz feleltethetö meg. A halmaz elemei az adott tulajdonság értékei, vagyis az egyedhalmazban szereplö egyedek ezen tulajdonsághoz tartozó értékei.
Például tekintsük a hallgató egyedhalmazt. A hallgató egyedtípust jellemezzük a hallgatókód, név, születési dátum, szak, évfolyam tulajdonságokkal. A név tulajdonságértékeinek halmaza az összes hallgató neve, a születési dátum tulajdonságértékeinek halmaza az összes hallgató születési idejének halmaza. Az évfolyam halmaz 5 elemböl áll (1, 2, 3, 4, 5), mert a hallgatók vagy az 1., vagy a 2., ... , vagy az 5. évfolyamra járnak.
A hallgatókód, név, születési dátum, szak, évfolyam halmazok közötti reláció azon ötösökböl áll, amelyek 1. eleme a hallgatókód, 2. eleme a név, 3. eleme a születési dátum, 4. eleme a szak, 5. eleme az évfolyam halmazból származik. Pl.: (1234, Nagy Judit, 1971.07.11, magyar, 2)
Ez a reláció ötödfokú. Természetesen a relációt alkotó ötösök a lehetséges ötösöknek csak egy részhalmaza, mégpedig azok, amelyek valamely egyed tulajdonságait írják le. Így ezek az ötösök az öt halmaz, illetve azok elemei közötti összefüggéseket fejezik ki.
A reláció tehát n-esekböl áll. Ezeket elrendezhetjük táblázatos formában úgy, hogy egy-egy n-es lesz a táblázat egy-egy sora. Vagyis egy sor egy egyed tulajdonságértékeit tartalmazza. A táblázat oszlopai az egyes tulajdonságok, például név oszlop, születési dátum oszlop. Egy oszlopban az adott tulajdonságérték-halmaz valamely eleme szerepelhet. A táblázat könnyen áttekinthetö, a felhasználó számára természetes megjelenése az adatoknak.
Azt az adatmodellt, amely az adatok táblázatos ábrázolásán alapul, relációs adatmodellnek nevezzük. A relációs adatmodellben minden egyes reláció egy névvel ellátott táblázat.
Az adatmodell elemeinek megfeleltethetök a reláció elemei:
A reláció tartományai a tulajdonságok. A táblázatban a tartományoknak az oszlopok felelnek meg. Minden egyes oszlopnak önálló neve van, az oszlopokat adattípusukkal és méretükkel jellemezhetjük. Így a tarományok a hagyományos adatfeldolgozás adatmezöinek felelnek meg. A sorok egy-egy egyed tulajdonságértékeit tartalmazzák. A sorok a hagyományos adatfeldolgozás rekordjainak megfelelöi. Az egyedhalmaz megfelelöje pedig maga a táblázat.
A reláció definíciójából következnek a tulajdonságai:
- Minden sorban, minden oszlophoz egyetlen érték van hozzárendelve., vagyis a táblázat minden cellájában egy elemi érték szerepel. Ez abból következik, hogy a reláció elemeit úgy képeztük, hogy 1 halmazból pontosan 1 értéket vettünk.
- A sorok és oszlopok sorrendje a modell szempontjából közömbös.
Hiszen a reláció képzésénél tetszölegesen választhatjuk meg, hogy a tulajdonsághalmazok milyen sorrendben szerepeljenek, a reláció elemeit szintén tetszöleges sorrendben rendezhetjük egymás alá, amikor táblázatot alkotunk belölük. A modell adattartalma nem változik meg ha a sorok, vagy az oszlopok sorrendjét megváltoztatjuk.
- Egy relációban nem lehet két teljesen azonos sor.
Az adatmodellben egy egyedhalmazban nem lehet két teljesen azonos tulajdonságokkal rendelkezö egyed, a definíció szerint a reláció elemei között sem lehet két teljesen azonos n-es.
- Minden relációban kiválasztható a tartományoknak legalább egy olyan kombinációja, melyeknek tartalma egyértelmüen egyetlen sort határoz meg. Ezt a tartományt (oszlopot), vagy tartománycsoportot nevezzük az adott reláció kulcstartományának. Amennyiben a kulcstartomány csak egyetlen tulajdonságból áll, akkor egyszerü kulcsról beszélünk, egyébként pedig összetett kulcsról.
Mivel az egyedhalmaz rendelkezett kulccsal, a megfelelö reláció szintén rendelkezni fog vele. A kulcstartományok az egyedhalmaz kulcsát alkotó tulajdonságoknak megfelelö oszlopok lesznek.
A gyakorlatban elöfordul, hogy egyes egyedek valamely tulajdonságértékét nem ismerjük, ezért megengedjük, hogy egy sorban valamely oszlopban, vagy oszlopokban ne szerepeljen érték. (Vagyis üres érték szerepeljen. Az üres értéket szokás NULL értéknek nevezni.)
Tekintsük a következö példát:
Egy raktári nyilvántartásban a raktárakban található anyagokról a következö adatok szerepelnek:
raktárszám, cikkszám, megnevezés, mennyiség, egységár.
Készítsünk egy Raktár táblát, amelynek oszlopai ezek a tulajdonságok. Az anyag megnevezése és az egységára annyiszor szerepel a táblázatban, ahány raktárban az adott anyag megtalálható. Ha egy anyag egységára megváltozik, ez minden olyan sort érint, amely erre az anyagra vonatkozik. Ha egy anyag kifogy a raktárakból, akkor ennek az anyagnak a megnevezése és egységára sehol sem fog szerepelni a táblában. Ha újra érkezik ebböl az anyagból valamelyik raktárba, az anyag jellemzöit újra fel kell vinni valahonnan. Ezen problémák kiküszöbölésére célszerü a táblázatban szereplö tulajdonságok összefüggéseinek elemzése, és a táblázatok átalakítása normál formájú táblázatokká.
Elsö normál forma
Azon relációkat, amelyek ábrázolhatók táblázatos formában és minden sor és oszlop metszéspontjában csak egyetlen érték (elemi érték) található, elsö normál formájúnak (1NF) nevezzük.
Funkcionális függöség
Egy relációban az A tulajdonság funkcionálisan függ a B tulajdonságtól (vagy tulajdonságcsoporttól), ha B értéke egyértelmüen meghatározza A értékét.
Például a felsöoktatási intézményeket a következö tulajdonságokkal írjuk le:
név, cím, a vezetö (rektor, föigazgató) neve, hallgatói létszám
Az oktatási intézmény neve egyértelmüen meghatározza az intézmény vezetöjének nevét, ezért a vezetö neve funkcionálisan függ az intézmény nevétöl.
Teljes függés
Amennyiben A tulajdonság funkcionálisan függ a B tulajdonságcsoporttól, az A tulajdonság teljesen függ a B tulajdonságcsoporttól, ha csak a teljes B tulajdonságcsoporttól függ, de annak részeitöl nem.
Vagyis a teljes B tulajdonság-csoport egyértelmüen meghatározza az A tulajdonság értékét, azonban a B tulajdonság-csoport bármely összetevöje önmagában nem határozza meg A értékét.
Például egy élelmiszer-áruházban a vásárlásokról a következö adatokat tartják nyilván: a pénztárgép számát, a vásárlás dátumát és idöpontját, valamint a fizetett összeget.
A pénztárgép száma, a vásárlás dátuma és idöpontja együttesen egyértelmüen meghatározza a fizetett összeget, azonban a pénztárgép száma önmagában nem határozza meg, hiszen egy pénztárgépen nagyon sok vásárlást blokkolnak, a dátum és az idöpont sem határozza meg egyértelmüen, hogy melyik vásárlásról van szó, mert egy adott idöpontban több pénztárgép is blokkolhat. Tehát a vásárláskor fizetett összeg teljesen függ a pénztárgép száma, a vásárlás dátuma és idöpontja tulajdonságcsoporttól.
Második normál forma
Azon relációkat, amelyek elsö normál formában vannak és minden olyan tulajdonság, amely nem elsödleges kulcs teljesen függ az elsödleges kulcstól, második normál formájúnak (2NF) nevezzük. Ez tulajdonképpen azt jelenti, hogy a lehetö legszükebb tulajdonságcsoportot választottuk kulcsnak.
Ha egy reláció elsö normál formájú, és minden kulcsa egyszerü kulcs, akkor második normál formájú is. Az egyszerü kulcs egyetlen tulajdonságból áll, ezért itt nem fordulhat elö, hogy valamely tulajdonság csak a kulcs egy részétöl függ.
Tranzitív függés
Egy relációban egy A tulajdonság tranzitíven függ a B tulajdonság(csoport)tól, ha van olyan C tulajdonság(csoport), amely teljesen függ B-töl és az A pedig teljesen függ C-töl, de B nem függ C-töl és C nem függ A-tól.
Vagyis, ha egy relációban egy tulajdonság funkcionálisan függ az elsödleges kulcstól, de olyan tulajdonságtól is függ, amely nem része a kulcsnak, ezt nevezzük tranzitív függésnek.
Például:
A dolgozók napi munkadíj-elszámolását egy táblázatban tartjuk nyilván, melynek oszlopai (a tulajdonságok):
dátum, személyi szám, órabér, dolgozott órák száma, fizetés
A kulcs a dátum és a személyi szám. A fizetés azonban függ az órabértöl és a dolgozott órák számától, ezért ez a reláció tranzitív függést tartalmaz.
Harmadik normál forma
Azon relációkat, amelyek második normál formában vannak és nem tartalmaznak tranzitív függöséget (vagyis minden tulajdonság csak az elsödleges kulcstól függ), harmadik normál formájúnak (3NF) nevezzük.
Az elsö normál formájú relációk csak egy része teljesíti a második normál forma feltételeit, ezeknek pedig csak egy része teljesíti a harmadik normál forma feltételeit.

Bebizonyítható, hogy minden reláció elöállítható 3NF relációk összességeként. Azt az eljárást, amelynek segítségével egy reláció harmadik normál formájú relációkká alakítható, normalizálásnak nevezzük. Egy reláció normalizálását általában további relációkra történö bontással valósíthatjuk meg.
Egy reláció további relációkra történö bontásán azt értjük, hogy a kiinduló táblázat helyett kisebb táblázatokat alakítunk ki úgy, hogy a létrejövö táblázatok együttesen ugyanazt az információtartalmat hordozzák, mint a kiinduló táblázat.

A normalizálási eljárás az adatbázistervezés témakörébe tartozik, ezért ebben a könyvben csak egy példán keresztül szemléltetjük, hogy hogyan bontható részekre egy reláció. Sem az algoritmussal nem foglalkozunk, sem annak bizonyításával, hogy az így kapott relációk együttese pontosan azt az adattartalmat hordozza, mint a kiinduló reláció.
A feladatunk a hallgatók adatainak nyilvántartása. Elsö közelítésben adatainkat a következö táblázatban ábrázolhatjuk:
HALLGATÓK
(HALLGATÓKÓD, SZÜLETÉSI DÁTUM, NÉV, KAR, SZAK, ÉVFOLYAM, TANTÁRGYKÓD, TANTÁRGYNÉV, TANTÁRGY KREDITÉRTÉKE, JEGY, TANÁRKÓD, TANÁR NEVE, TANSZÉK NEVE)
Egy sor egy hallgató adatait és vizsgajegyeit tartalmazza.
A táblázat kulcsa a hallgatókód. A név nem lehet kulcs, mert egy oktatási intézményben elöfordulhatnak azonos nevü hallgatók és tanárok, ezért volt szükség a hallgatókód, és a tanárkód bevezetésére. Két különbözö tanszék is meghirdethet azonos nevü tantárgyat, így célszerübb a tantárgyakat is kóddal azonosítani.
Mivel egy hallgató több tantárgyat tanul egy félévben, a táblázatban egy hallgatóhoz több tantárgyra vonatkozó tulajdonságérték (tantárgykód, tantárgy neve stb.) tartozhat. Tehát ez a tábla nem normalizált.
Alakítsuk át úgy a táblázatot, hogy egy sorban csak egy tantárgy szerepeljen, vagyis minden hallgatóhoz annyi sor tartozzon, ahány tantárgyat hallgat az adott félévben. Az így kapott tábla sorait már nem azonosítja egyértelmüen a hallgatókód, ezért a hallgatókódot és a tantárgykódot választjuk kulcsnak. A tábla így elsö normál formában van.
Vizsgáljuk meg, hogy milyen összefüggések vannak a tulajdonságok között:
Csak a hallgatókódtól függ: születési dátum, név, kar, szak, évfolyam
Csak a tantárgykódtól függ: tantárgynév, tantárgy kreditértéke, tanárkód, tanár neve, tanszék neve
A teljes kulcstól függ: jegy
Ennek megfelelöen bontsuk három táblára a kiinduló táblánkat. Az elsö táblában helyezzük el a hallgatóra vonatkozó tulajdonságokat, a másodikban a tantárgyakra vonatkozókat. A harmadikba kerül a jegy, amelyik függ a hallgatókódtól és a tantárgykódtól, ezért mindkét kódnak szerepelnie kell benne.
HALLGATÓ-1
(HALLGATÓKÓD, SZÜLETÉSI DÁTUM, NÉV, KAR, SZAK, ÉVFOLYAM)
A kulcs a hallgatókód.
TANTÁRGY
(TANTÁRGYKÓD, TANTÁRGYNÉV, TANTÁRGY KREDITÉRTÉKE, TANÁRKÓD, TANÁR NEVE, TANSZÉK NEVE)
A kulcs a tantárgykód.
EREDMÉNY
(HALLGATÓKÓD, TANTÁRGYKÓD, JEGY)
A hallgatókód és a tantárgykód alkotja a kulcsot.
A kapott táblák második normál formában vannak, mert az elsö két tábla kulcsa egyszerü kulcs, a harmadik táblában a jegy tulajdonság pedig az összetett kulcs mindkét tagjától függ. Hiszen csak a hallgatókód ismeretében nem tudom megmondani, hogy milyen jegyet kapott a hallgató. Csak a tantárgykód ismeretében sem lehet tudni a jegyet, mert számos hallgató kaphatott jegyet abból a tantárgyból.
A HALLGATÓ-1 és az EREDMÉNY tábla harmadik normál formájú, a tulajdonságok csak a kulcstól függnek. A TANTÁRGY tábla azonban nem harmadik normál formájú, mert a tanár neve és a tanszék függ a tanár kódjától, ami pedig nem kulcs. Ezért ezt a táblát bontsuk két újabb táblára, úgy, hogy a tanárra vonatkozó adatokat emeljük ki egy másik táblába:
TANTÁRGY-1
(TANTÁRGYKÓD, TANTÁRGYNÉV, TANTÁRGY KREDITÉRTÉKE, TANÁRKÓD)
A kulcs a tantárgykód.
TANÁR
(TANÁRKÓD, TANÁR NEVE, TANSZÉK NEVE)
A tábla kulcsa a tanárkód.
Az így kapott táblák már harmadik normál formában vannak.
A normalizálási eljárás eredményeként a kiinduló táblánkat négy táblára bontottuk:
HALLGATÓ-1
EREDMÉNY
TANTÁRGY-1
TANÁR
Most vizsgáljuk meg, milyen elönyök származnak ebböl a felbontásból, a 3NF táblázatok használatából.
Sokkal kevesebb adat kerül többszörösen tárolásra (minimális redundancia).
A tantárgyakat leíró adatok (név, kreditérték) csak egyszer kerülnek tárolásra a TANTÁRGY-1 táblában, míg az eredeti táblánk esetén annyiszor tároltuk öket, ahány hallgató felvette az adott tantárgyat.
Ha módosítani kell egy tantárgy valamely adatát, például a kreditértéket, elegendö ezt egyetlen helyen elvégezni.
A kiinduló tábla esetén, ha minden olyan hallgatót törlünk a táblából, akik egy adott tantárgyat felvettek, akkor a tantárgy adatai is törlödnek. Míg a harmadik normál formában levö tábláink esetén a TANTÁRGY-1 táblában benne maradhat az a tantárgy, amelyet abban a félévben nem oktatnak, így a rá vonatkozó adatok nem vesznek el a törlés során.
Rugalmasabb adatfelvitelt biztosít, hiszen ha egy új tantárgyat szeretnénk bevezetni, már akkor is felvihetjük az adatait a TANTÁRGY-1 táblába, amikor még egyetlen hallgató sem vette fel. Ezt a kiinduló tábla esetén nem tehetjük meg.
A továbbiakban csak olyan relációkkal foglalkozunk, melyek harmadik normál formában vannak.
Az elöbbi példánkban a kiinduló táblánkat négy táblára bontottuk. A kapott táblák egymással kapcsolatban állnak, kulcsmezöiken keresztül. Az EREDMÉNY tábla a hallgatókód segítségével kapcsolódik a HALLGATÓ-1 táblához, a tantárgykód segítségével pedig a TANTÁRGY-1 táblához. A TANÁR tábla a tanárkódon keresztül áll kapcsolatban a TANTÁRGY-1 táblával.
A relációs adatbázisban egyes táblázatok - többnyire kulcsmezöiken keresztül - kapcsolatban állhatnak egymással. A relációs adatbázisok terminológiájában szokásos a táblázat sorait azonosító kulcstartományt elsödleges kulcsnak (primary key) nevezni. Azt a tartományt pedig, amely az adott táblázatban szerepel, és egy másik táblázatban kulcstartomány, idegen kulcsnak (foreign key) nevezik.
Elözö példánkban a TANÁR táblában a tanár kódja elsödleges kulcs, hiszen ebben a táblában egyértelmüen meghatároz egy sort egy tanárkód érték. A TANTÁRGY-1 táblában a tanárkód nem kulcs, mert értéke nem határoz meg egyértelmüen egy sort, hiszen egy tanár több tantárgyat is taníthat, így több sorban is szerepelhet a kódja. A TANTÁRGY-1 táblában a tanárkód idegen kulcs, mert egy másik tábla, mégpedig a TANÁR tábla elsödleges kulcsa.
Egy relációnak több kulcsa is lehet, ekkor döntés kérdése, hogy melyiket választjuk elsödleges kulcsnak.
A relációs adatmodellben mind az 1:N mind az N:M típusú kapcsolatokat ki tudjuk fejezni. A táblázatos forma elönye, hogy jól áttekinthetö, sokkal könnyebb benne eligazodni, mint a kusza hálózatokban. Minden hálózat - esetleg bizonyos redundanciák bevezetésével - táblázattá alakítható, vagyis mind a hierarchikus, mind a hálózatos adatmodell átalakítható relációs adatmodellé.
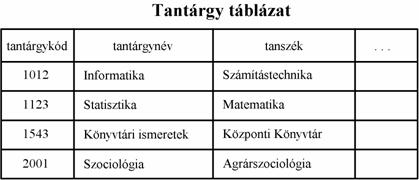
Nézzük meg a hálós adatbázisoknál bemutatott hallgatók és tantárgyak nyilvántartását és vessük össze a normalizálási példában bemutatottal. A hallgatók és tantárgyak nyilvántartását három táblázattal célszerü megvalósítani. Az elsö a Hallgató tábla, mely az egyes hallgatók adatait tartalmazza, a második a Tantárgy tábla, amely a tantárgyakra vonatkozó adatokat tartalmazza, a harmadik pedig a Kapcsolat tábla, amelynek két oszlopa van, az egyik a hallgatókód, a másik a tantárgykód, sorai az összetartozó hallgatókód-tantárgykód párokat tartalmazzák. Vagyis egy hallgatókód annyiszor szerepel benne, ahány tantárgyat hallgat, egy tantárgykód pedig annyiszor, ahány hallgató hallgatja. Amennyiben a tantárgyból kapott jegyet is felvesszük a tulajdonságok közé, úgy ez is a Kapcsolat táblába kerül. Ekkor a Kapcsolat tábla a normalizálási példában az Eredmény táblának felel meg. Mivel a hálós adatbázisoknál alkalmazott feladatban a tanárokra vonatkozó adatok nem szerepeltek, a normalizálási példa Tanár táblájának nincs megfelelöje.
A Hallgató táblázatban a hallgatókód a kulcs, hiszen ez az érték azonosítja egyértelmüen a hallgatót. A Tantárgy táblázatban a tantárgykód a kulcs, a Kapcsolat táblázatban pedig a hallgatókód és a tantárgykód alkotják a kulcsot.


Ugyanazon adatbázis különbözö felhasználóinak az egyedhalmazokról és a közöttük levö kapcsolatokról eltérö felfogása lehet, ezért egyes felhasználók számára a táblázat oszlopainak részhalmazait kell kiemelni, más felhasználók számára pedig a táblázatokat össze kell vonni, létrehozva ezzel egy magasabb rendü táblázatot. A relációs modell egyik nagy elönye, hogy a különbözö igényeknek megfelelö adatelemek matematikailag könnyen és jól definiálhatók a relációalgebra, vagy a relációanalízis segítségével.
A relációalgebrai müveletek olyan müveletek, melyek relációkon vannak értelmezve, s eredményük szintén reláció. Tekintsük át a legfontosabb relációalgebrai müveleteket.
Projekció (vetítés). Egy R reláció T1, T2, ... , Ti tartományokra történö vetítésének eredménye az a reláció, melyet R-böl úgy kapunk, hogy csak a felsorolt oszlopokat vesszük a táblázatból. Jelölése: PT1,T2,...,Ti(R)
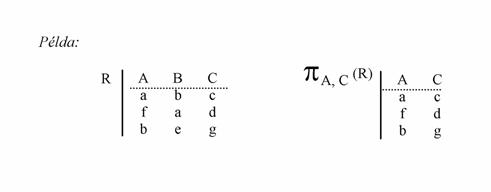
Például: A hallgatók adatait tartalmazó táblából csak a hallgatók nevét és az évfolyam számát szeretnénk látni.
Szelekció (korlátozás) . Egy R reláció F feltétel szerinti korlátozása az a reláció, melyet R-böl úgy kapunk, hogy csak az F feltételt kielégítö sorait hagyjuk meg. Az F feltétel oszlopnevekböl, konstansokból, logikai müveletekböl és összehasonlító operátorokból épül fel. Jelölése: sF(R)
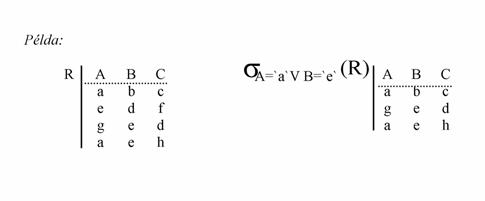
Például: A hallgatók adatait tartalmazó táblából csak azokat a hallgatókat szeretnénk látni, akik a 3. évfolyamra járnak. A szelekció feltétele évfolyam=3 .
Egyesítés (unió) . Az R és S relációk egyesítése azon sorok összessége, melyek vagy az R, vagy az S relációban benne vannak. Az esetleges azonos sorok csak egyszer szerepelnek az unióban. Ez a müvelet csak azonos sorhosszúságú relációkon értelmezhetö. Jelülése: R U S
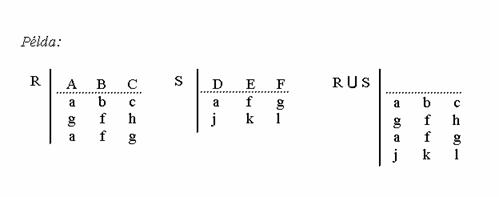
Például: Az egyik tábla tartalmazza a Mezögazdaságtudományi Kar hallgatóinak nevét, születési dátumát, lakcímét, a másik ugyanolyan felépítésü tábla a Gazdaság- és Társadalomtudományi Kar hallgatóinak adatai. A két kar hallgatóinak adatait tartalmazó táblát a két tábla egyesítésével kapjuk meg. Azon hallgatók, akik beiratkoztak mindkét karra, csak egyszer fognak szerepelni az eredménytáblában.
Különbség. Egy R és S reláció különbsége azon sorokból áll, melyek benne vannak R-ben, de nincsenek benne S-ben. Az R és S relációnak azonos sorhosszúságúnak kell lennie. Jelölése: R - S
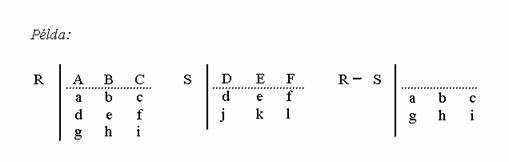
Például: Az egyik tábla tartalmazza a Mezögazdaságtudományi Kar hallgatóinak nevét, születési dátumát, lakcímét, a másik ugyanolyan felépítésü tábla a Gazdaság- és Társadalomtudományi Kar hallgatóinak adatai. Azon hallgatók adatait, akik csak a Mezögazdaságtudományi Karra járnak úgy kaphatjuk meg, hogy az elsö táblából kivonjuk a második táblát.
Metszet. Egy R és S reláció metszete azokat a sorokat jelenti, melyek mindkét relációban benne vannak. Jelölése: R S
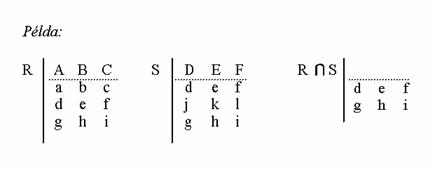
Például: Az egyik tábla tartalmazza a Mezögazdaságtudományi Kar hallgatóinak nevét, születési dátumát, lakcímét, a másik ugyanolyan felépítésü tábla a Gazdaság- és Társadalomtudományi Kar hallgatóinak adatai. A két tábla metszete azon hallgatók adatait tartalmazza, akik mindkét karra beiratkoztak.
Direkt szorzat. Ha egy R reláció sorai r elemböl állnak, egy S relációé pedig s elemböl, akkor a két reláció direkt szorzataként kapott reláció sorai r+s elemböl fognak állni, úgy, hogy a sor elsö r eleme egy R-beli sor, utolsó s eleme pedig egy S-beli sor, s ezek minden lehetséges összeállításban szerepelnek. Ha R-ben k db sor volt, S-ben pedig n db, akkor a direkt szorzat eredményeként kapott relációban k*n db sor lesz! Jelölése: R X S
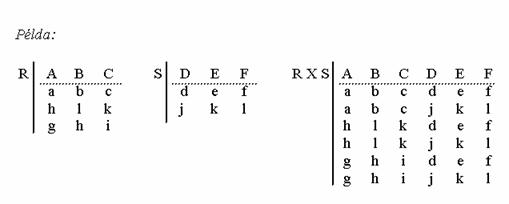
Például: Az egyik tábla tartalmazza a könyvtár szak 1. évfolyamára járó hallgatók nevét és születési dátumát. A másik tábla a könyvtár szakon az 1. félévben oktatott vizsgaköteles tárgyak nevét és óraszámát. Egy olyan táblázatot szeretnénk készíteni, amelyben minden egyes 1. éves könyvtár szakos hallgatóról szerepel, hogy milyen vizsgákat kell letennie. Ezt a két tábla direkt szorzataként tudjuk elöállítani. Az eredménytábla oszlopai a hallgatók nevét, születési dátumát, a tantárgy nevét és óraszámát fogják tartalmazni. Az eredménytábla sorainak száma annyi lesz, amennyi a hallgatók száma szorozva a tantárgyak számával.
Összekapcsolás (join) . Legyen R és S két reláció, valamint tekintsünk egy összehasonlító operátort. Az R és S reláció összekapcsolása az a reláció, amelyet az R x S relációból úgy kapunk, hogy csak azokat a sorokat hagyjuk meg, amelyekben az R reláció i-edik és az S reláció j-edik oszlopa között fennáll az összehasonlító operátornak megfelelö reláció.
Ha a megadott reláció egyenlöség, akkor az összekapcsolást egyenlöség-összekapcsolásnak (equijoin) nevezzük. Jelölése: R * S
i Q j
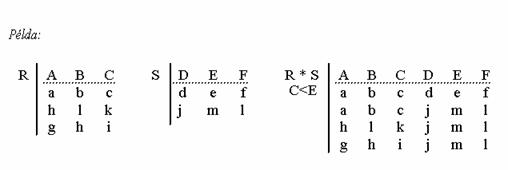
Például: Az egyik tábla gyerekek nevét és zsebpénzét tartalmazza. A másik tábla az üzletben kapható játékok nevét és árát. Egy gyerek csak olyan játékot vásárolhat meg, amelynek ára nem több, mint a saját zsebpénze. Tudni szeretnénk, hogy melyik gyerek melyik játékokat veheti meg. Ehhez készítsük el a két tábla összekapcsolását, amelynek feltétele, hogy a zsebpénz oszlopban található érték nagyobb, vagy egyenlö legyen az ár oszlopban található értéknél. Vagyis a két tábla direkt szorzatából csak azokat a sorokat vesszük, ahol zsebpénz>=ár .
Természetes összekapcsolás (natural join) . Legyen R és S két reláció. Állítsuk elö R x S -t és csak azokat a sorokat hagyjuk meg, melyek R és S azonos nevü tartományain megegyeznek. Vagyis, az azonos mezökben azonos érték található. Az azonos mezökböl csak egyet-egyet hagyunk meg. Az így kapott eredményreláció a két reláció természetes összekapcsolása. Jelölése: R * S
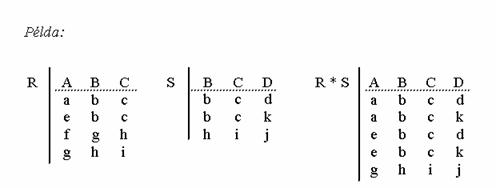
Például: Az egyik tábla tartalmazza a hallgatók nevét, születési dátumát, a szak kódját és az évfolyamot. A másik táblázat a szak kódját és nevét tartalmazza. Olyan táblázatot szeretnénk készíteni, amelyben a hallgatók adatai mellett nemcsak a szak kódja, hanem a neve is szerepel. Készítsük el a két tábla természetes összekapcsolását. Az azonos oszlop a szak kódja, ez az eredménytáblában csak egyszer fog szerepelni. Minden hallgatóhoz annak a szaknak a neve lesz hozzákapcsolva, amelyikre jár, vagyis amelyik szak kódja megegyezik a hallgató táblázatban feltüntetett szakkóddal.
Ha egy táblában idegen kulcsként szerepel egy másik tábla kulcsa, akkor a két tábla természetes összekapcsolása ennek a kulcstartománynak a segítségével történhet. A normalizálásnál bemutatott példában a TANTÁRGY-1 és a TANÁR tábla természetes összekapcsolásához a tanár kódját használhatjuk.
Az eredménytábla a következö lesz:
(TANTÁRGYKÓD, TANTÁRGYNÉV, TANTÁRGY KREDITÉRTÉKE, TANÁRKÓD, TANÁR NEVE, TANSZÉK NEVE)
A relációanalízis segítségével a felhasználó
azt az eredményt definiálja, amit az adatbázisból kapni kíván. A megfogalmazott
feltételekkel sorokat, vagy mezöket lehet kiválasztani. A feltételek
definiálásához a mezöneveket, konstansokat, összehasonlító operátorokat,
logikai müveleteket (és, vagy, negálás), továbbá a "létezik" és
a "
és
vagy
negálás
létezik
" minden
Példák
Egy hallgatói nyilvántartásból keressük ki a harmadik évfolyamból azokat a csoportokat, amelyekben volt olyan hallgató, aki jeles eredményt ért el. Ennek megfogalmazása: azon csoportokat választjuk ki, amelyekre igaz, hogy az évfolyam értéke 3 és létezik 4.5-nél jobb eredmény:
Egy hallgatói nyilvántartásból keressük ki a harmadik évfolyamból azokat a csoportokat, amelyekben minden hallgató eredménye jobb volt, mint 3.5 . Ennek megfogalmazása: azon csoportokat választjuk ki, amelyekre igaz, hogy az évfolyam értéke 3 és minden eredmény jobb, mint 3.5 :
A relációanalízis és a relációalgebra egymással egyenértékü. Bármely relációanalízissel felírt kifejezést megfogalmazhatunk relációalgebrai formulákkal és ez fordítva is igaz. Egyes relációs adatbáziskezelök lekérdezö nyelve a relációalgebrán alapul, vannak azonban a relációanalízisre támaszkodó nyelvek is, söt olyanok is, amelyek mindkettöt támogatják. A relációanalízis müveleteinek segítségével a felhasználó a kívánt adatokat tulajdonságaik alapján választhatja ki, míg a relációalgebrai müveletek esetében az adatok elöállításához szükséges müveleteket kell megadni.
Találat: 1706