| kategória | ||||||||||
|
|
||||||||||
|
|
||
A CURIE-ELV
Pierre Curie mondta ki először a szimmetriamegmaradásnak azt a fontos következményét, ő érzett rá először arra, hogy egy-egy effektusnak nemcsak a szimmetriája a fontos, hanem az is, hogy milyen szimmetriák hiá 454i86e nyoznak belőle, azaz ő nevezte meg először konkrétan a diszszimmetria, azaz a szimmetriahiány fogalmát is. Hogyan kellene kiindulnunk ilyen formális módszerekkel az energiamegmaradás megkerülésére? Az eddigiekből az következik, hogy legalább két olyan kiváltó effektust kell keresni, amelyben az a követelmény, hogy mindkét effektusnál előálljon az energia meg nem maradása. A két effektus egymásrahatása, "összeházasítása" után várhatjuk csak azt, hogy kialakulhat ilyen hatás, ahol energiatöbbletünk vagy energiahiányunk lesz.
Itt most nagyon oda kell figyelni a szavak jelentésére. Amikor azt mondjuk, hogy olyan hatásokat kell keresni, ahol nem marad meg az energia, akkor nem azt állítjuk, hogy önmagában, különkülön is többlet vagy hiány keletkezik, csak azt a tényt, hogy egy effektus esetén is egy rendszerrel energiát tudunk közölni, vagy energiát tudunk kivenni egy rendszerből, azaz a rendszer nem tud zárt maradni. Ez csak nemkonzervatív rendszereknél fordulhat elő, s ilyen a gyakorlatban nagyon sok van, például a szélmalom vagy a hajócsavar is energiát vesz föl vagy ad le a környezetének. Az ingaóra, azaz egy konzervatív gravitációs térben mozgó test nem vesz föl a környezetéből energiát. Amint elengedtük az ingát, az megtartja eredeti energiaszintjét, csak a potenciális, azaz helyzeti energia alakul át periodikusan mozgási energiává és vissza.
Ha a súrlódási veszteségektől eltekintünk, akkor ez a folyamat a végtelenségig tartana, hiszen konzervatív erőtérben minden fizikai rendszer mindig megtartja eredeti energiáját. A nemkonzervatív rendszereknél, azaz például az örvényes, a sebesség- vagy időfüggő s emiatt nempotenciálos rendszereknél ez nem igaz, azok állandóan energiát tudnak fölvenni vagy leadni. Ezek után formális logikával gondolkozva már egyszerű az eredeti feladat megoldása.
 Keresnünk kell két
olyan rendszert, ahol nem potenciálos nem konzervatív erőterek vannak. A forgó,
örvényes rendszerek alkalmasak erre, vagy például a sebesség- és
időfüggő rendszerek. Ha például egy merev karon el tudunk húzni egy
súlyt úgy, hogy az erő értéke időben változik, akkor egy időfüggő, nem
potenciálos tér segítségével olyan rendszert valósítottunk meg, amelyben az
energia nem marad meg, hiszen az időben változó erő segítségével egyre több
vagy egyre kevesebb energiája lehet a rendszernek. Ha ugyanakkor ezt a
rendszert még meg is forgatjuk egy tengely körül, akkor az örvényes erőtér
segítségével megint csak nem potenciálos erőteret kapunk, azaz újra egy olyan
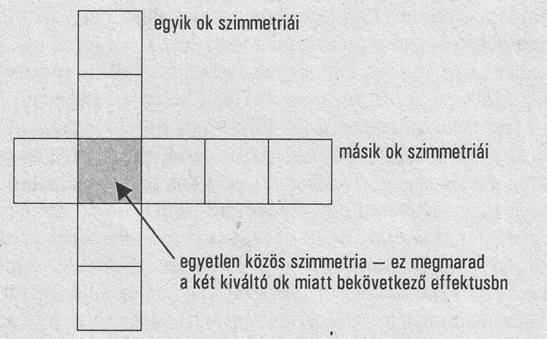
erőteret, amiben nem marad meg a rendszer energiája. Ha formálisan a II/3. ábrán megnézzük a két rendszer
szimmetriatulajdonságait, akkor azt látjuk, hogy a karos és a forgó rendszer
összehozható úgy, hogy csak egyetlen közös szimmetriájuk lesz, azaz az energia
meg nem maradása áll elő, és ez az új effektusban is megjelenik. Ha jól gondolkoztunk,
akkor egy sugárirányú, időfüggő mozgás, valamint egy tangenciális irányú
örvényes mozgás "összeházasításával
olyan rendszert kaptunk, ahol a megmaradó eredő szimmetria már nem tartalmazza
az energiamegmaradást, és ilyenkor lehet
akár energiatöbbletünk vagy -hiányunk is. Okunk van föltételezni, hogy így Orffyreus titkához jutottunk el, azaz így
például spirálmozgások, vagy más hasonló típusú, nem konzervatív erőterek által
okozott mozgások segítségével kaphatunk olyan hatást, ahol energia "termelődik vagy tűnik el.
Keresnünk kell két
olyan rendszert, ahol nem potenciálos nem konzervatív erőterek vannak. A forgó,
örvényes rendszerek alkalmasak erre, vagy például a sebesség- és
időfüggő rendszerek. Ha például egy merev karon el tudunk húzni egy
súlyt úgy, hogy az erő értéke időben változik, akkor egy időfüggő, nem
potenciálos tér segítségével olyan rendszert valósítottunk meg, amelyben az
energia nem marad meg, hiszen az időben változó erő segítségével egyre több
vagy egyre kevesebb energiája lehet a rendszernek. Ha ugyanakkor ezt a
rendszert még meg is forgatjuk egy tengely körül, akkor az örvényes erőtér
segítségével megint csak nem potenciálos erőteret kapunk, azaz újra egy olyan
erőteret, amiben nem marad meg a rendszer energiája. Ha formálisan a II/3. ábrán megnézzük a két rendszer
szimmetriatulajdonságait, akkor azt látjuk, hogy a karos és a forgó rendszer
összehozható úgy, hogy csak egyetlen közös szimmetriájuk lesz, azaz az energia
meg nem maradása áll elő, és ez az új effektusban is megjelenik. Ha jól gondolkoztunk,
akkor egy sugárirányú, időfüggő mozgás, valamint egy tangenciális irányú
örvényes mozgás "összeházasításával
olyan rendszert kaptunk, ahol a megmaradó eredő szimmetria már nem tartalmazza
az energiamegmaradást, és ilyenkor lehet
akár energiatöbbletünk vagy -hiányunk is. Okunk van föltételezni, hogy így Orffyreus titkához jutottunk el, azaz így
például spirálmozgások, vagy más hasonló típusú, nem konzervatív erőterek által
okozott mozgások segítségével kaphatunk olyan hatást, ahol energia "termelődik vagy tűnik el.
Az előbbi okoskodás persze nagyon formális, és csak akkor hihető el, ha kísérletileg is meg tudjuk erősíteni. Látni fogjuk azonban ezután, hogy szinte az összes találmány erre az alapeffektusra épül. Addig azonban még érdemes egy újabb rövid sétát tennünk, meg kell néznünk, hogy a matematikában hogyan fejlődött a szimmetria fogalma, hiszen mindaddig, amíg a matematika kristálytiszta logikájával elő nem áll ez a fogalom, addig sem a fizika, sem a technika nem tud igazán nagyot előrelépni. Azért is érdemes a matematika oldaláról is megnézni az energia, az impulzus és impulzusnyomaték és a szimmetria összekapcsolódását, mert ott is a fenti hasznos eredményre lehet jutni, csak más úton.
1I/3. ábra: A Curie féle szimmetria kivonási szabály elve: Két kiváltó ok esetén csak az a szimmetria marad meg a bekövetkezett hatásban, amely közös mindkét ok esetén.
Találat: 1733