SZIMMETRIÁK MEGMARADÁSA

SZIMMETRIÁK MEGMARADÁSA

Úgy gondolnánk, hogy mind az elektromos tér, mind a mágneses tér egy azonos matematikai mennyiséggel, vektorral írható le. Mindkét térerősségnél az erőnek van iránya és nagysága is, tehát látszólag nyugodtan használhatunk azonos típusú vektort a két mező leírására. Ez a felszínes hasonlóság azonban megtévesztő, és ez is egyik oka volt annak, hogy mintegy nyolc évi kínlódás és kí­sérletezés után, és akkor is csak véletlenül jutott Oersted arra a kor­szakalkotó fölfedezésre, hogy az elektromosság és a mágnesesség egymással kapcsolatban van. Ha tudta volna Oersted, hogy az elektromosság poláris és a mágnesesség axiális vektorral írható le, és ismerte volna a szimmetria-műveleteket, valószínűleg nem nyolc év, hanem nyolc nap alatt, esetleg nyolc perc alatt elvégzi a sikeres kísérletet. Oersted persze annyival jobb volt pályatársainál, hogy legalább próbálgatta az elektromosság és mágnesesség közti kap­csolat megtalálását, míg a többiek belenyugodtak Cavendish és Coulomb tekintélyelvű kinyilatkoztatásába.

Nézzük meg, hogy milyen vektorok létezhetnek, mi a poláris és axiális vektor közti különbség, hogy jelenik meg ez a szimmetriák­ban. Ha a II/1. ábrát látjuk, akkor nyilvánvalóvá válik ez a különb­ség. Az axiális vektor lényegében egy forgó henger szimmetriájá­val jellemezhető. Amikor nyomatékot hozunk létre, például forga­tunk egy tengelyt, mindig axiális vektorok jelennek meg. Ennek a forgó tengelynek a szimmetriája, tükröződése azonban eltér a polá­ris vektor tükröződésétől, szimmetriájától. Látjuk, ha a forgásten­gellyel párhuzamos síkra tükrözzük az axiális vektort, akkor az megfordul, azaz antiszimmetrikussá válik. Abban az esetben vi­szont, ha a tengelyre merőleges síkra tükrözzük, akkor változatlan, azaz teljesen szimmetrikus marad.

Az antiszimmetria azért érde­kes, mert megmarad ugyan a vektor nagysága, csak előjele változik meg. A könnyebben elképzelhető poláris vektor (ami például az erő és a sebesség leírására is használatos) más tükrözési szimmetri­ákkal bír. Ha a poláris tengelyt a tengellyel párhuzamosan tükröz­zük, akkor változatlan marad, és ilyen esetben mondjuk, hogy a tükrözés szimmetrikus, azaz a tükrözés művelete mint transzformá­ció nem változtatja meg az eredeti állapotot, hanem változatlanul megy át a transzformáció után az új állapotba a régi állapot. Ilyen­kor nem tudjuk megkülönböztetni az eredeti és a transzformáció utáni állapotot.

Abban az esetben viszont, ha tengelyre merőlege­sen tükrözünk, akkor antiszimmetrikus tükörképet kapunk, mely­nek nagysága azonos ugyan, de előjele megváltozik. Az Oersted­kísérlet esetén egy olyan esetet vizsgálunk meg, ahol két különbö­ző szimmetriatulajdonsággal rendelkező ok váltja ki a számunkra értékes hatást. Kétségtelen, hogy ez bonyolultabb eset mintha csak egyetlen szimmetria, egyetlen kiváltó fizikai hatás változik, de egyúttal szemléletesebb is.

Nézzük meg, hogy a szimmetriamegmaradás törvénye hogyan alkalmazható egy gyakorlati esetre. A II/2. ábrán látszik az az eset, amikor Oersted a sikertelen kísérleteket végezte. Helyezzük bele egy-egy szimmetriasíkba a drótot, azaz az áramot, majd erre merőleges síkba a mágnestűt, azaz a mágneses tér irányát.

Látjuk például, hogy a s sík, mely az iránytű mágneses terének szim­metriáját tartalmazza, anti szimmetrikus a mágnesességre nézve, hiszen itt a tengellyel párhuzamos síkra kell tükröznünk. Abban az esetben is anti szimmetrikus transzformációt kapunk, ha az erre a síkra merőleges I áramot tükrözzük. Az előbbiek során ugyanis láthattuk, hogy a síkra merőleges tükrözés esetén a poláris vekto­rok anti szimmetrikusak lesznek. Ezért azt látjuk, hogy a s síkban anti szimmetrikus lesz mindkét vektor.

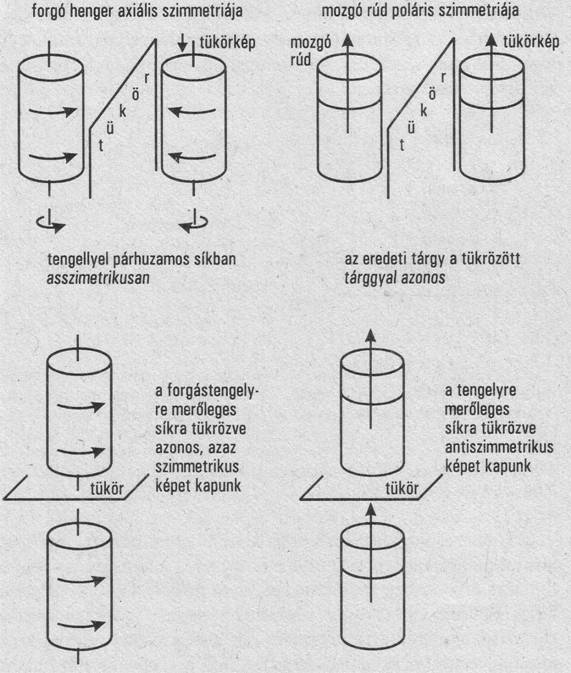II/1 1. ábra: Forgó henger és mozgó rúd tükrözési szimmetriái. A mágneses mező szimmetriája axiális, az áram szimmetriája poláris.

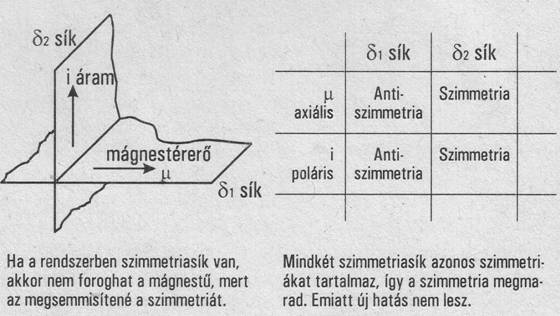Nézzük meg most a s -vel jelzett síkban mi történik. Látjuk, hogy az I áramra rásimuló szimmetriasík esetén a mágneses vektor axiális szimmetriája megmarad, tehát szimmetrikus transzformáci­ót kapunk, és ugyanez a helyzet az árammal is, hiszen az áram irá­nyával párhuzamos maga a szimmetriasík, tehát szimmetrikus transzformációt kapunk. Vagyis tükrözés után mindkét síkban megmarad a szimmetria, éppen ezért összeegyeztethetetlen bármi­féle forgással itt a szimmetriák esete, ezért nem is remélhetünk ef­fektust. Megmarad a szimmetria mindkét síkban, hiszen az egyik síkban csupa anti szimmetrikus, a másik síkban csupa szimmetrikus transzformációt találunk. Ott, ahol megmarad a szimmetria, ott bi­zony változás sincs, ez a szimmetriamegmaradás törvényének egyik következménye.

II/2a. ábra: Ha az i áram is a ,m mágneses mező egymásra merőleges, ak­kor mindkét szimmetriasíkban azonos szimmetriák lépnek fel. Emiatt nincs hatás, semmi sem történik.

Más lesz a helyzet azonban, ha a II/2b. ábrát nézzük, ahol egy­mással párhuzamos az áram is és a mágneses térerősség is. Tegyük fel, hogy a s síkba simul mind az áram poláris, mind a mágneses tér axiális vektora. Ebben az esetben a s síkban, mely erre merőle­ges, azt találjuk, hogy a mágneses térerősség axiális vektora szim­metrikus transzformációval megy át, mig az áram poláris vektora anti szimmetrikus transzformációval megy át. Így ebben a síkban kétféle szimmetriát is találunk. Ugyanez lesz a helyzet a s síkkal is, itt is az axiális vektor, a mágneses térerősség antiszimmetrikus transzformációval megy át, míg az áramerősség szimmetrikus transzformációval megy át, hiszen az áram irányával párhuzamos lesz a szimmetriasík.

Látjuk, hogy itt mindkét síkra két különböző szimmetria jellem­ző, azaz mindkét oknak, mindkét effektusnak más-más szimmetriá­ja van. Ebben az esetben nem marad meg a tükrözés után a szim­metria, így viszont már előfordulhat a szimmetriasíkot megbontó forgási művelet, forgási operáció vagy transzformáció.

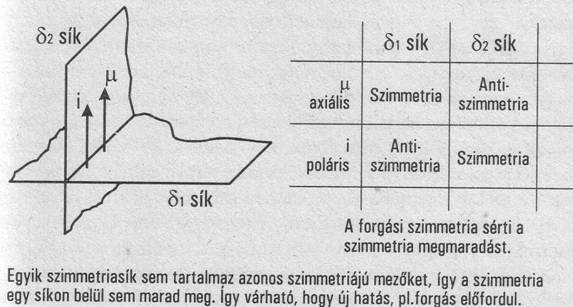Ekkor már elvileg létrejöhet a forgás. Természetesen Oersted annak idején nem tudta, hogy létezik poláris és axiális szimmetria, és nem tudta, hogy az áramerősség poláris, míg a mágneses térerősség axiális szimmetriával bír. Ez a kísérlet azonban alkalmas lett volna annak eldöntésére, hogy a két mennyiség nem azonos szimmetriával ren­delkezik, azaz eltérő tulajdonságaik vannak.

II/2b. ábra: Ha az i áram is a p mágneses mező egymással párhuzamos. akkor egy-egy szimmetriasíkban más-más szimmetriájú mező lép fel Ekkor nem marad meg a szimmetria, így várható hogy fellép valamilyen hatás, pl. elforul a mágnestű.

A távírót megcsinálhatták volna már az egyiptomiak, a rómaiak, de akár a kínaiak vagy az indiaiak is, technikailag voltak olyan szinten, hogy ezt létrehozzák. (Más kérdés, hogy Morse-ábécét csak a latin vagy orosz ábécével lehetett volna létrehozni, a kínai­val vagy az indiaival nehezen.) Hiányzott azonban a "minőségi gondolkodás", ami elsősorban csak egy maroknyi protestáns gon­dolkodású országban terjedt el, ott is csak lassan és döcögve.

Azt gondolnánk, hogy Oersted kíséréletéből levonták kortársai ezt a nagy tanulságot, hogy a szimmetriákat kísérletileg érdemes meg­állapítani, és nem íróasztal mellett kiagyalni. A kísérlet sok-sok vajúdás után sikeres lett, ám a megfelelő következtést senki nem vonta le. Ez a tanulsága egy másik hasonló esetnek is, ami az in­dukcióval kapcsolatos, és gyakorlati hatásait nézve ugyanolyan fontos, mint az Oersted kísérlet. Ez a Faraday-Henry-féle indukciós kísérlet. Ez a kísérlet egyszerűbb, mint az Oersted-féle hatás, hi­szen itt mindössze egyetlen szimmetriát, a mágneses térerősség időbeli állandóságát, szimmetriáját kellett csökkenteni. Itt mind­össze egyetlen kiváltó ok létezik. Így a szimmetria kivonási sza­bályt nem tudjuk alkalmazni, de az általános elv itt is létezik: egy szimmetria megszüntetése új jelenségeket idéz elő.

Faraday Angliában, Henry pedig az Egyesült Államokban találta meg az indukció hatását szintén nyolcévnyi kísérletezés után: Az alapeffektus itt is nagyon egyszerű: ha egy szolenoidból kirántunk egy mágnest, vagy bármi más módon időben változtatjuk a mágne­ses teret, akkor a szolenoidban elektromos áram indukálódik. Ez a nagyon egyszerűnek tűnő effektus egyáltalán nem volt kézzelfog­ható, egyáltalán nem volt magától értetődő abban a korban, és nem véletlen, hogy évekig nem jöttek rá. Az előző példában, Oersted kísérletében a két kiváltó ok más és más térbeli szimmetriát muta­tott.

Nemcsak a térbeli, hanem időbeli szimmetriát is lehet változ­tatni, csökkenteni. Képzeljük csak el, hogy az idő függvényében fölírjuk egy mágnes körül, minden egyes pontban a mágneses térerősség értékét. Ha egy időpillanatban ezt megváltoztatjuk, ak­kor csökken ennek a rendszernek a szimmetriája. Az állandó térerősség ugyanis egy térbeli és időbeli szimmetriát ad, hiszen bármely más időpontban állandó a térerősség iránya és nagysága. Ez egy időbeli eltolási szimmetriát eredményez, hiszen változatlan a térerősség, és a változatlanság, az invariancia a kulcsszó a szim­metria megértésében. Természetesen Faraday idejében még nem gondolkodtak a szimmetria segítségével (hiszen ma sem használják még mankóként sem a szimmetria kiterjesztett fogalmát).

Ez azért tragikus, mert ha ebből a két igen hasznos effektusból, ennek tanulmányozásából levonják a megfelelő következtetést, ak­kor újra vissza lehetett volna térni az energia megvizsgálására, ki­derülhetett volna, hogy az energia is egy szimmetria, és mint min­den szimmetria, ez is csökkenthető.

Ha másként nem, legalább formális logikával, okoskodással el lehetett volna jutni ahhoz a gondolathoz, hogy az energia értéke nem szükségszerűen állandó. Azt láttuk ugyanis eddig legalább két ok esetén, hogy a szimmetria akkor marad meg például, ha egy jelenséget előidéző mindkét ki­váltó okban egyszerre található meg ugyanaz a szimmetria. Ebben az esetben az okozatban, a jelenségben is megmarad ez a szimmet­ria, de csak ez a szimmetria. Azok a szimmetriák, amelyek nem közösek a két kiváltó okban, azok "kiesnek", mintegy kivonódnak. Ezt a megfigyelést lehetett volna használni az energia mint szim­metria csökkentéséhez, megszüntetéséhez. Ez az út vezet az "in­gyenes" többletenergia előállításához.