Sztatikus terek

1. Az örvénymentes - forrásos tér tárgyalása (skalárpotenciál)

Az örvénymentes-forrásos tereket általánosan a következö két egyenletböl alkotott egyenletrendszer írja le:

Mivel egy vektortér gradiensével származtatott vektortér rotációja, függetlenül az eredeti vektortértöl, minden esetben azonosan nulla (, 5. Matematikai függelék), a vektor felírható egy skalártér gradienseként, , (ahol a negatív elöjelet a késöbbi fizikai alkalmazások kedvéért használjuk) a (1) egyenletrendszer második egyenlete a következö alakban írható fel:

Behelyettesítjük a -t a (1) egyenletrendszer elsö egyenletébe:

Descartes-koordinátákban,

Általános esetben tehát az örvénymentes-forrásos teret leíró skalárpotenciált a Laplace- vagy Poisson egyenlet (másodrendü, lineáris parciális differenciálegyenlet) megoldásával határozhatjuk meg.

Keressük a fenti Laplace-egyenlet megoldásait, amelyek a tér véges helyzetü pontjaiban mind regulárisak, a végtelenben viszont meghatározott (elöírt) módon nullához tartanak. Tekintsük a 1 ábrát, ahol egy zárt felület (S) által elhatárolt térfogatban (V) ismerjük a mennyiséget. Feladatunk meghatározni a skaláris mennyiséget az ábrán feltüntetett V térfogatban található pontban. A feladatot a skalárfüggvényekre érvényes Green-tétellel oldható meg (6. Matematikai függelék).

ahol, a keresett potenciálfüggvény, skalárfüggvény pedig tetszölegesen megválasztható, de meg kell feleljen a Gauss-tételnél elöírt követelményeknek.

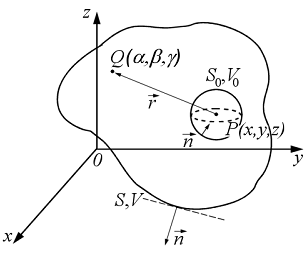
1 ábra

Válasszuk a skalárfüggvényt úgy, hogy az feleljen meg a 1 ábrán látható P pont és Q futópont (mely bejárja a teljes V térfogatot, beleértve a P pontot is) közötti távolság moduluszával.

Természetesen választásunkat úgy végeztük, hogy számításaink a lehetö legegyszerübbek legyenek, amit úgy érhetünk el, hogy a (5) egyenletben szereplö legyen egyenlö nullával. Vizsgáljuk meg, hogy az általunk választott függvény megfelel-e ennek a követelménynek. Már a definícióból kitünik, hogy ha a Q pont egybeesik a P ponttal , tehát -nek szingularitása van. Számítsuk ki értékét kirekesztve a P pontot a tárgyalásból. Alkalmazzuk a Laplace-operátort a skalárfüggvényre, mely azt jelenti, hogy elöször ki kell számoljuk a függvény gradiensét, majd a kapott vektortér divergenciáját (5. Matematikai függelék 9. Feladat):

A (8) egyenlet azt jelenti, hogy ha a skalárfüggvényre alkalmazzuk a Laplace-operátort, minden a P pontok kívüli pontban nullát kapunk. Mivel a P pont szingularitást jelent, a továbbiakban kirekesztjük a V térfogatból, mégpedig úgy, hogy azt körbevesszük egy sugarú, felületü és térfogatú gömbbel. Eszerint a Green-tétel érvényes lesz az így kapott, kívülröl, az S, belülröl pedig az S₀ felület által határolt térfogatra.

A továbbiakban meg kell vizsgáljuk az egyenlet jobb és bal oldalán lévö integrálok viselkedését a P pontot kirekesztö gömb sugarának nullához való tartatásakor ().

A (9) egyenlet felületen számított integrál második tagjának becsléséhez figyelembe kell vennünk, hogy az integrált az felületen kell végezzük vagyis , tehát,

majd alkalmazzuk az integrálszámítás középértéktételét (vagyis a függvénynek tekintjük a középértékét arra a felületre vonatkozóan, és azt kiemeljük az integrál elé, majd kiszámítjuk a megmaradt integrált, amely a gömb felületét adja:

Ez az eredmény azt jelenti, hogy amikor , a fenti integrál is tart zéróhoz.

A (9) egyenlet felületen számított integrál elsö tagjának becsléséhez hasonlóan járunk el, de figyelembe kell vennünk, hogy az irány szerint kell deriváljuk a függvényt és a irány az felületü gömb középpontja felé mutat. Áttérünk a irány szerinti deriválásra, amely és figyelembe vesszük, hogy , tehát:

Ez az eredmény azt jelenti, hogy amikor , a potenciál középértéke kell tartson a keresett pontban lévö potenciálhoz, vagyis

A (9) egyenlet bal oldalán lévö integrálról meg kell még gyözödni, hogy nem fog divergálni abban az esetben amikor . Ehhez tekintsük a 2 ábrát, írjuk fel a térfogategységet a poláris koordinátákban és végezzük az alábbi becslést:

Ez az eredmény azt jelenti, hogy annak ellenére, hogy az -ban az integrál alatti kifejezés divergens, az integrál értéke a pontban tart nullához, amikor .

A fenti számításokat figyelembe véve a (9) egyenlet a következöképpen írható fel, amely megadj a keresett pontban a potenciál értékét.

Megjegyzés: nem szabad elfeledkeznünk arról, hogy a fenti összefüggésben a deriváltak és integrálások mind a futópont koordinátái szerint történnek.

Ez az összefüggés azt jelenti, hogy ha adott egy ismert skalárfüggvény egy adott S zárt felület által határolt V térfogatban (pl. elektrosztatikában egy töltéseloszlás), amely egyben a keresett potenciálfüggvény Laplace - operátorával egyenlö, akkor kiszámíthatjuk a potenciál értékét a V térfogatban, ha adott a potenciál és deriváltja az S felületen.

A potenciál és deriváltjának értékét viszont nem választhatjuk meg tetszölegesen. Ha ezt tesszük, a potenciál értékét kiszámíthatjuk a V térfogat minden pontjában, az eredmény eleget tesz majd a Laplace-egyenletnek, viszont az S felületen nem kapjuk vissza a potenciálnak általunk elöírt értékét. Hogy ezt elkerüljük, toljuk ki a határfelületet a végtelenbe és tekintsük az egész végtelen teret.

Ha elvárjuk azt, hogy a potenciál a végtelenbe legalább függvény szerint tart nullához (ahol a vizsgált pont és az igen távoli futópont közötti távolság, pedig egy tetszöleges pozitív szám), akkor a deriváltja szerint tart nullához. Ennek megfelelöen, a (15) egyenletben a felületi integrálok szerint tartanak nullához, így a végsö eredményt a (16) egyenlettel adhatjuk meg:

vagy,

Az elektrosztatikus tér

Az 1. Fejezetben meghatároztuk az elektrosztatika egyenleteit (18), ahol az ismert töltéseloszlás, mely lehet folytonos vagy diszkrét jellegü is.

Ennek az egyenletrendszernek ugyanaz az alakja, mint az örvénymentes-forrásos tereket leíró általános egyenletrendszeré (1). Meghatároztuk a 1 bekezdésben, hogy ebben az esetben a térerösség vektor megadható egy skaláris potenciál gradienseként, vagyis , ahol az elektrosztatikus potenciál. Behelyettesítjük -t a (18) egyenletrendszer elsö egyenletébe:

Descartes-koordinátákban,

A 1. bekezdésben elvégzett számítások alapján, a (20) egyenlet általános megoldását az alábbi alakban írhatjuk fel:

A fenti összefüggés alapján, bármilyen ismert töltéseloszlás esetében a tér egy adott pontjában meghatározható az elektrosztatikus potenciál értéke.

Tekintsünk egy a töltéseloszlástól nagy távolságra elhelyezkedö pontot. Ebben az esetben a tekintett pont, a töltéseloszlás bármely pontjától jó megközelítéssel azonos távolságúnak tekinthetö. Ebben az esetben a (21)-el adott integrál alól az távolság kihozható és az alábbi összefüggéshez jutunk,

ami nem más, mint a pontszerü töltés által létrehozott elektrosztatikus potenciálra távolhatási szemléletmóddal kapott eredmény. Kiszámíthatjuk a létrehozott elektromos teret is (23).

Ez viszont magába hordozza a Coulomb-kölcsönhatást is (24).

A fenti számítások igazolják az 1. Fejezet 1.3. Közelhatás-távolhatás címü bekezdésében tett kijelentéseket, melyek szerint az elektromágneses tér közlehatási szemlélete magába hordozza a távolhatási szemléletmóddal kapott eredményeket is.

3. A forrásmentes - örvényes tér tárgyalása (vektorpotenciál)

A forrásmentes-örvényes tereket általánosan a következö két egyenletböl alkotott egyenletrendszer írja le:

Mivel egy vektortér rotációjával származtatott vektortér divergenciája, függetlenül az eredeti vektortértöl, minden esetben azonosan nulla (, 5. Matematikai függelék), a (25) egyenletrendszer második egyenletéböl következik, hogy az vektor divergenciája nulla kell legyen () az vektor pedig felírható egy vektortér rotációjaként, , a (25) egyenletrendszer elsö egyenlete a következö alakban írható fel:

Behelyettesítjük az -t a (25) egyenletrendszer második egyenletébe:

Ezt az összefüggést az 5. Matematikai függelék szerint írhatjuk, mint.

tehát,

Ezt az egyenletet könnyebben kezelhetö alakra lehet hozni, ha az divergenciájára megkötést írunk elö. Vizsgáljuk meg, miként lehet megkötést elöírni, az általánosság feltételeinek lazítása nélkül. Tekintsünk két különbözö vektorteret, és , amelyek ugyanazt az vektorteret generálják, tehát . Ebböl következik, hogy 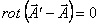. Viszont minden esetben egy skalártér gradiensével származtatott vektortér örvénymentes (5. Matematikai függelék, ), az és vektorok egy skalárfüggvény gradiensével különbözhetnek egymástól, és ugyanazt az vektort generálják.

Ez azt jelenti, hogy nem egyértelmüen értelmezett, ezért a számításaink egyszerüsítése érdekében válasszuk ki ezek közül azt a függvényt, amelynek a divergenciája nulla.

A (31) összefüggést figyelembe véve az (1.66) egyenletet a következö alakban írhatjuk fel:

Ez a vektoriális egyenlet az örvénymentes-forrásos tér (4) egyenletéhez hasonló, három skaláris összefüggésre bontható fel (5. Matematikai függelék).

Descartes-koordinátákban,

A fenti egyenletek azt jelentik, hogy komponenseit ugyanolyan Laplace-egyenletekböl határozhatjuk meg, mint az örvénymentes-forrásos térnél a skalárpotenciált. A megoldás menete ugyanaz, mint az elöbbi részben, ezért itt az eredményt írjuk fel:

Kiterjesztve a tárgyalást a végtelen térre:

4. A magnetosztatikus tér

Az egyenáram által létrehozott magnetosztatikai tér örvényes és forrásmentes, tehát a 3. bekezdés szerint lehet tárgyalni. A magnetosztatikai térre vonatkozó egyenletrendszer, a megfelelö mennyiségekkel a (37) egyenletrendszerrel írhatjuk le.

Az elözö pontnak megfelelöen a mágneses tér indukcióját megadhatjuk egy vektortér rotációjaként, ahol az újabb vektorteret vektorpotenciálnak nevezzük (38) és -al jelöljük.

Viszont egy vektortér ugyanazt a mágneses teret hozza létre (3. bekezdés). A megnetosztatikai számításoknál megköveteljük, hogy a vektorpotenciál gradiense nulla legyen, vagyis:

Az áramerösség segítségével meghatározhatjuk a vektorpotenciált,

amely az 5. Matematikai függelék 6. Feladata alapján,

amely (39) alapján

A (42) egyenlet ugyanazt a szerepet tölti be a magnetosztatikában, mint a (19) egyenlet az elektrosztatikában. Ennek az egyenletnek a megoldása (36) alapján történik, figyelembe véve a vezetörendszer geometriáját is.

A vektorpotenciál meghatározása után kiszámíthatjuk a mágneses tér indukcióját egyszerüen meghatározva ennek rotációját.

1. Az örvénymentes - forrásos tér tárgyalása (skalárpotenciál)

Az elektrosztatikus tér

3. A forrásmentes - örvényes tér tárgyalása (vektorpotenciál)

4. A magnetosztatikus tér.