| kategória | ||||||||||
|
|
||||||||||
|
|
||
Véges determinisztikus és nemdeterminisztikus automaták.Ekvivalenciájuk és kapcsolatuk a reguláris nyelvekkel. Mealy- és Moore-automaták.
Véges automaták, mint felismerők
Véges automaták: formális nyelvek ( ezen belül reguláris nyelvek ) felismerőinek viszonylag egyszerű matematikai modelljei.
![]()
![]()
![]()
![]()
![]()
![]()
![]() Szemléltetés:
Szemléltetés:
![]() a1 a2 ...... an-1 an
a1 a2 ...... an-1 an
![]()
![]() bemenő
szalag
bemenő
szalag
 (rajta
egy szó a megengedett
jelekből.)
(rajta
egy szó a megengedett
jelekből.)
Véges állapotú
vezérlőmű
(véges belső
állapottal)
Működés:
Az automata beolvas egy jelet balról jobbra a bemenő szalagról. Ettől és az aktuális belső állapotától függően egy másik belső állapotba kerül. ( Determinisztikus automata esetén ez az állapot egyértelműen meghatározott )
Indulás: kezdő állapotból
Befejezés: ha kiürült a bemenő szalag.
- Ha az automata befejezéskor végállapotba kerül felismerte a szót.
- Az automata által felismert nyelv: az automata által felismert szavak halmaza.
Példa: 3-mal osztható számok:
![]() 0,3,6,9
0,3,6,9
![]()
 A0
A0

 2,5,8 2,5,8
2,5,8 2,5,8
![]() 1,4,7
1,4,7
![]()
![]() A2
A2
![]()
![]() A1
A1
![]() 2,5,8
2,5,8
0,3,6,9 0,3,6,9
A0: kezdőállapot
A0: végállapot
Állapotok halmaza: A0, A1, A2
Működés a = 1104 szó esetén:
![]() 1 1 0 4
1 1 0 4
![]()
![]()
![]()
![]() A0 A1 A2
A2 A0
A0 A1 A2
A2 A0
Végállapotba került: a 3-mal osztható.
Automaták (determinisztikus) általános definíciója:
A = < A,T,a0,F,d >
|A| < ¥ : belső állapotok halmaza
|T| < ¥ : bemenő jelek halmaza (bemenő abc)
a0 A : kezdőállapot
F A : végállapotok halmaza
d: A×T A : átmenetfüggvény
Példa: (Előbbi)
d(A0,1)= A1
d(A1,1)= A2
d(A2,0)= A2
d(A2,4)= A0
Kérdés: A0 F
Definíció: d kiterjesztése:
d': A×T* A
( Bemenő jelek sorozatára mondja meg, hogy milyen állapotba jutunk. )
d'(a,e) = a ![]() a A
a A
d'(a,pt) = d d'(a,p),t) , p T*, t T
Megjegyzés: Tehát a,b A, w T* esetén d'(a,w)=b azt jelenti, hogy az a állapotból az automata w szót elolvasva b állapotba jut.
Más definíció: q:= t1 t2 ... tk ti T
d' (a,q) = b Û ![]() c0, c1,..., ck A c0=a,
ck=b és d(c0, t1) = c1,
d(c1, t2)= c2,
... ,d( ck-1, tk)= ck
.
c0, c1,..., ck A c0=a,
ck=b és d(c0, t1) = c1,
d(c1, t2)= c2,
... ,d( ck-1, tk)= ck
.
Definíció: Az u T* szót az A automata elfogadja, ha d'(a0,u) F
Definíció: A által elfogadott nyelv:
L(A):=
Definíció: A 1 ekvivalens A 2-vel, ha L(A 1 ) = L(A 2 )
Példa: A2 := < , , q0 , , d >
d(q0,a)= q1 d(q0,b)= s
d(q1,a)= q1 d(q1,b)= q2
d(q2,a)= q1 d(q2,b)= q2
d(s,a)= s d(s,b)= s
bemenő jelek
Megadás:
![]()
![]()
![]()
 1., Táblázattal: a b
1., Táblázattal: a b
![]()
![]()
q0 q1 s d
![]() állapotok
állapotok
q1 q1 q2
![]()
q2 q1 q2
![]()
s s s
2., Átmeneti diagrammal:
Ez egy
irányított gráf, melyben ![]() állapot egy csúcsnak
felel meg.
állapot egy csúcsnak
felel meg.
p q él
létezik (p,q A ) , ha ![]() a T d(q,a)=q .
a T d(q,a)=q .
Ekkor p q élre ráírjuk a-t.
( p q élet "színezzük" a-val. )
![]() Végállapot
jele:
Végállapot
jele:
![]() Kezdőállapot
jele: bemutató nyíl
Kezdőállapot
jele: bemutató nyíl
![]()
 a
a
q0 a q1 q2
![]()
![]()
![]()
![]()
![]()
 a b a b b
a b a b b
![]()
![]() s
s
b
Mely szavakat fogadja el ?
- az üres szót,
- a-val kezdődő és a-val végződő szavakat.
![]() Ekvivalens automata:
Ekvivalens automata:
![]() a
a

 a
a
![]()
![]() q0 a q1 q2
q0 a q1 q2
![]()
![]() b b
b b
Példa: A:= < , , a0 , , d >
![]()
![]()


 a Xa a
a Xa a

![]()
![]()
![]() d a b a,b,c,d
d a b a,b,c,d
![]()
![]()
 d b c a b
d b c a b
![]()
![]() a0 Xb s
a0 Xb s
![]() d
d
![]()
![]()

 c b c
c b c
d Xc
c
Mely szavakat fogadja el ?
Melyekben a d-n kívül kettő, vagy több egyforma betű nem szerepelhet egymás mellett.
![]()
![]()
![]()
![]()
d a b c d
![]()
a0 Xa Xb Xc a0
Xa s Xb Xc a0
![]()
![]()
![]()
Xb Xa s Xc a0
Xc Xa Xb s a0
![]()
s s s s s
Példa: A:= < , , q0 , , d >
![]()

![]()
![]() d a b a
d a b a
![]()
![]()
![]() q0 b
q0 b
![]()
![]()
 q0 q1 q2 a b
q0 q1 q2 a b
![]() q0 q0
q0 q0
![]() q1 q0 q2 a
q1 q0 q2 a
![]()
![]()
q2 q1 q0 b
Mely szavakat fogadja el ?
Ahol a szó végén nem áll páros számú azonos betű.
Lemma (Bar-Hillel)
Legyen adott L nyelv, melyet egy determinisztikus véges automata felismer.
Ekkor ![]() n N ha a L szóra d(a ³ n , akkor a előállítható a=uvw alakban, ahol d(uv)
n N ha a L szóra d(a ³ n , akkor a előállítható a=uvw alakban, ahol d(uv) ![]() n , d(v) ³ 1
és
n , d(v) ³ 1
és ![]() i= 0,1,2,.. term.
számra: uviw L.
i= 0,1,2,.. term.
számra: uviw L.
Példa:
u1 := abc ca ab u2 := abc caca ab
u v w u v2 w
Megjegyzés: n konstansnak választható az L-t felismerő automata belső állapotainak száma.
Köv.1.: Legyen A determinisztikus automata és belső állapotainak száma: n.
Az A által felismert nyelv nem üres Û ![]() n-nél rövidebb szó, melyet A felismer.
n-nél rövidebb szó, melyet A felismer.
Köv.2.: Van olyan algoritmus, mely eldönti egy véges determinisztikus automatáról, hogy az általa felismert nyelv üres-e.
Köv.3.: Van olyan környezetfüggetlen nyelv,
amelyhez ![]()
Példa: G1 = < , , s , >
G1 környezetfüggetlen
L(G1) =
Állítás: ![]()
Bizonyítás: Indirekt
T.f.h. ![]() ilyen A. Ekkor a Bar-Hillel-lemma alapján megfelelően nagy
m-re:
ilyen A. Ekkor a Bar-Hillel-lemma alapján megfelelően nagy
m-re:
am bm = uvw , ahol d(v) ³ 1 és tetszőleges i= 0,1,2,...-re uviw L(G1).
De: - ha v a és b betűt is tartalmaz, akkor uv2w L(G1) , mert a betűk sorrendje megbomlik.
(pl.: aaa abb bb aaa abbabb bb )
u v w u v2 w
- ha v csak a betűt tartalmaz, akkor uw L(G1) (i=0) , mert a szóban kevesebb a van, mint b.
- ha v csak b betűt tartalmaz, hasonlóan.
Nemdeterminisztikus véges
automaták
Különbség: Egy belső állapotból több olyan él is indulhat, mely azonos betűvel van "színezve".
Szó felismerése: (ugyan az, mint véges det. automatáknál)
u szót az automata
felismeri, ha ![]() a gráfban irányított
út kezdőállapotból indul, végállapotba jut és az élek rendre u
betűivel vannak színezve.
a gráfban irányított
út kezdőállapotból indul, végállapotba jut és az élek rendre u
betűivel vannak színezve.
Pontos definíció: ( nemdet. aut. )
A = < A , T , a0 , F , d >
A: belső állapotok véges, nem üres halmaza
T: bemenő abc
a0: kezdőállapot (a0 A )
F A végállapotok halmaza
d: A x T 2A , azaz d(q,a)= , ahol a T és q, p1, ... pl A
Működés:
! u= t1 t2 ... tk T* szó.
Az automata pillanatnyi állapota : q
1. lépés: d(q,t1) =
2. lépés: lehetséges állapotok halmaza:
d(p1, t2)È d(p2, t2)È È d(pl, t2)
....
Végigolvassuk az u szót és ha végül a lehetséges állapotok halmazában van végállapot, akkor A felismerte u-t.
Definíció: d kibővítése szóra:
d' : A x T* 2A
1., d'(q,e ![]() q A
q A
2., d'(q,wa)=
![]()
![]() q A , w T* , a T
q A , w T* , a T
Definíció: Az automata által felismert nyelv:
L(A):=
Példa:
![]()
![]()
![]()
![]()
![]()
 d 0 1 1
d 0 1 1
![]() 0 q1 0
0 q1 0
![]()
 q0 0
q0 0
![]()
![]()
![]()
![]() q0 1
q0 1
q1 0 0

![]()
q2 0 q2 0
Működése a 0101 szóra:
1., d(q0,0) =
2., d'(q0,01) = d(q1, 1)Èd(q2, 1) = 0 È
3., d'(q0,010) = d(q1, 0) =
4., d'(q0,0101) =d(q0, 1)Èd(q1, 1) = È
Mivel q0 Ï F, a szót az automata nem fogadja el.
Definíció: GA :=
GND :=
Tétel: GA = GND
Bizonyítás:
GA GND
Triviális, hiszen ![]() determinisztikus automata felfogható speciális
nemdeterminisztikus automataként.
determinisztikus automata felfogható speciális
nemdeterminisztikus automataként.
GND GA
Konstruktív bizonyítás:
Legyen A:= < A,T,a0,F,d > véges, nemdeterminisztikus automata.
Ehhez konstruálunk egy vele ekvivalens véges determinisztikus automatát.
Legyen A' := < Q,T,t0,F',d' > véges determinisztikus automata a következő:
q := 2A ( A részhalmazai )
T uaz.
t0 :=
F' :=
d d'(H,a)=H' , ha H,H' Q, a T
H = pi A és H' ri A és = d(p1,a)È d(p2,a)È È d(pl,a)
Azaz d'(H,a) := ![]() d(pi,a)
d(pi,a)
Ekkor belátható ( u hosszára vonatkozó teljes indukció és d d' T*-ra vonatkoztatott kiterjesztése alapján), hogy:
![]()
![]() pi A , H 2A , u T*
esetén.
pi A , H 2A , u T*
esetén.
Belátjuk, hogy egy u T* szót pontosan akkor fogadja el az A nemdeterminisztikus automata, amikor A' determinisztikus automata elfogadja.
u L(A) Û d(a0,u) F ¹ Û
|| d' def. szerint
d'(,u)
|| t0 def. szerint
d'(t0,u)
Û d'(t0,u) F ¹ Û d'(t0,u) F' Û u L (A')
F' def. szerint
Példa :
A2 := < , ,q0, , d > véges nemdet. aut.
![]()

![]()
![]() d a b a a
d a b a a
![]()
![]()
![]()
q0 q0 b q1 a
![]()
![]()
![]() q1 0 b
q1 0 b
A2': Q = 0, , ,
¯ ¯ ¯ ¯
t[0] t[q0] t[q1] t[q0 ,q1]
T =
t0 = B t[q0]
F' = ¹
A2' = < ,,t[q0] , , d' >
![]()
![]() d' a b
d' a b
![]()
t[0] t[0] t[0]
![]()
t[q0] d(q0,a)= t[q0] d(q0,b)= t[q0,q1]
![]()
t[q1] d(q1,a)= t[q0,q1] d(q1,b)=0 t[0]
![]()
t[q0 ,q1] d(q0,a)È d(q1,a)=È t[q0,q1] d(q0,b)Èd(q1,b) =
È t[q0,q1 ]
![]()
![]()
![]()
![]()
 a b a
a b a


t[0] t[q0] t[q0] t[q0,q1]

![]()
![]()
![]()
![]() a b
a b
a
b b
Egyszerűsítve:
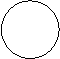
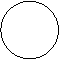
![]()
![]() t[q0] t[q0,q1
]
t[q0] t[q0,q1
]
![]()
![]() b a,b
b a,b
a
Minden szót felismer, amely tartalmaz b betűt.
Példa: 2., A3 := < , , A, , d >
![]()
![]()
![]() d 0 1
d 0 1
![]()
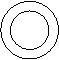
![]() 0 0
0 0
![]()
![]() A A B
A A B
![]()
![]() 1
1
![]() B
B
0 1
A3' < , , t[A], , d'>
d 0 1
t[0] t[0] t[0]
t[A] d(A,0)= t[A,B] d(A,1)= t[B]
t[B] d(B,0)= t[B] d(B,1)= t[A]
t[A,B] d(A,0)Èd(B,0)= d(A,1)Èd(B,1)=
È È
t[A,B] t[A,B]
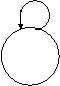

t[0] t[A] t[B] t[A,B]
![]()
![]()
elhagyható
Tétel: G3 = GA, azaz A nemdeterminisztikus (ill.: a determinisztikus) véges automaták osztálya megegyezik a reguláris nyelvek osztályával.
Bizonyítás: 1. irány: G3 GND(=GA) , azaz belátjuk, hogy ha L reguláris nyelv, akkor található véges nemdet. automata felismeri L nyelvet.
Legyen L reguláris nyelv, melyet a G = < T,N,S,P > nyelvtan generál.
Az A nemdet. automata definíciója:
A = < A,T,a0,F,d >, ahol
- A := NÈ , E Ï TÈN
- a0 := S
- d(B,a)= , B,Di A , a T ha P-ben szerepel az alábbi szabály: B aDi
E , ha P-ben szerepel a B a szabály.
- d(E,a)=0 ![]() a T
a T
- F=, ha P-ben nem szerepel az S e szabály, F= különben.
Könnyen megfontolható, hogy ez az automata L(G)-t ismeri fel.
Példa: w := ai1 ... aik L.
Ekkor P-ben szerepelnek az alábbi szabályok:
S ai1A1 ; A1 ai1A2 ; ... ; Ak-2 ai(k-1)Ak-1 ; Ak-1 aik
Tehát az automata definíciója szerint:
A1 d(S,ai1), A2 d(A1,ai2), ... , Ak-1 d(Ak-2,ai(k-1))
E d(Ak-1,aik) Þ E d(a,ai1 ... aik) Þ E d(S,w), azaz w L(A), mivel E végállapot.
Példa G:=< ,S,P >
P : S aS bS aA
A bB
B a
A hozzá tartozó automata: A < ,S, d >
|
d |
a |
b |
|
S |
|
|
|
A |
Æ |
|
|
B |
|
Æ |
|
E |
Æ |
Æ |
![]()
![]() b
b
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() S a A b B a E
S a A b B a E
![]()
![]()
![]() a
a
L(G) = L(A) = w w w aba
Bizonyítás (folytatás)
GA G 3
Azaz minden L nyelvhez, melyet egy véges det. automata felismer, minden olyan reguláris grammatika, mely az L nyelvet generálja.
Bizonyítás
A := < A,T,a0,F,d > véges det. automata, mely L-t felismeri. Ehhez konstruáljuk a következő G:= <T,N,S,P> reguláris grammatikát, ahol:
T := T
N := A
S := a0
P : - minden d(q,a) =p -hez tartalmaz egy q ap szabályt. (q,p A, A T)
- Ha d(q,a)=p esetén p F, akkor tartalmaz még egy q a szabályt is.
Állítás Ekkor L(G) = L(A) - e
Ui. 1. w = ai1.....aik L(A)
Ekkor az állapotok sorozata: d(a0,a1)=qi, d(qi1,ai2)=qi2, ......, d(qik-1,aik)=qik F
G szabályainak megadása miatt léteznek az alábbi szabályok: q0 ai1qi1, ..... , qik-1 aik
Tehát w levezethető G-ben.
![]()
![]()
![]()
![]()
![]() A
levezetés: q0 ¾ ai1qi1 ¾ ai1ai2qi2 ¾ ... ¾ ai1...aik-1qik-1 ¾ ai1...aik=w
A
levezetés: q0 ¾ ai1qi1 ¾ ai1ai2qi2 ¾ ... ¾ ai1...aik-1qik-1 ¾ ai1...aik=w
Azaz w L(G).
2. Visszafelé hasonlóan okoskodva: w L(G) Þ w L(A)
Megjegyzés
Ha e L(A), akkor az előzővel ekvivalens olyan grammatikát kell készíteni, ahol a0' az új kezdő szimbólum, mely nem szerepel szabály jobb oldalán és az új szabály: a0' e
Példa A = < ,q0, d>
|
|
a |
b |
|
q0 |
q1 |
q2 |
|
q1 |
q0 |
q2 |
|
q2 |
q1 |
q0 |
![]()
![]()
![]()
![]()
![]()
![]() a a
a a
![]()
![]()
![]()
![]()
![]()
![]() q0 a q1 b q2
q0 a q1 b q2
![]()
b
b
Milyen szavakat fogad el ? Szó végén nem állhat páros számú azonos betű.
A grammatika, mely ezt a nyelvet generálja: G:= < ,q0,P >
P : q0 aq1 q0 a
q0 bq2 q0 b
q1 aq0
q1 bq2 q1 b
q2 aq1 q1 a
q2 bq0
Véges automaták, mint formális nyelvek átalakítói
![]()
![]() a1 a2 ............................. ak-1 ak bemenő
szalag
a1 a2 ............................. ak-1 ak bemenő
szalag

 olvasófej
olvasófej
véges állapotú
vezérlőmű
![]()
![]() írófej
írófej
![]()
![]() kimenő szalag b1 b2 ............................. bk-1 bk
kimenő szalag b1 b2 ............................. bk-1 bk
![]()
Működés:
- kezdőállapotból indul
- elolvas egy jelet a bemenő szalagról (balról jobbra)
- új belső állapotba kerül és leír egy jelet a kimenő szalagra (balról jobbra)
Befejeződés:
- nincs definiált következő lépés
- elolvasta a bemenő szót
Mealy - automata
(A kimenő jel függ a belső állapottól és a beolvasott jeltől egyaránt.)
M: = <A, V, W, d l, q0 >, ahol: - A: belső állapotok véges, nem üres halmaz
- V: bemenő ábécé (V ¹ Æ, véges halmaz)
- W: kimenő ábécé (W ¹ Æ, véges halmaz)
- d átmenetfüggvény d:A V A
- l kimeneti függvény l: A V w
- q0: kezdőállapot q0 A.
Működés: a1a2......ak bemenő szóra
1. lépés: q1:= d(q0,a1) új belső állapot meghatározása
b1:=l(q0,a1) első kimenő jel meghatározása
2. lépés: q2:= d(q1,a2)
b2:=l(q1,a2)
:
:
Eredmény:
b1b2.....bk = l(q0a1)l(q1,a2).......l(qk-1,ak) W* szó
Definíció: M automata az a = a1....ak bemeneti szót b = b1....bk kimeneti szóvá fordította le. Jelölése: b=M(a
Definíció: Az M automata az L1 formális nyelvet L2-vé alakítja (fordítja le), ha
L2 =
Megadás: - táblázattal
- gráffal
Példa M1:=< d l, q0>
d(q0,a)= q0 l(q0,a)=0
d(q0,b)= q1 l(q0,b)=1
d(q1,a)= q1 l(q1,a)=1
d(q1,b)= q0 l(q1,b)=0
Táblázattal:
|
d l |
a |
b |
|
q0 |
q0,0 |
q1,1 |
|
q1 |
q1,1 |
q0,0 |
Gráffal: b/0
![]()
![]()
![]() q0 q1
q0 q1
![]()
![]()
![]()
![]()
![]()
![]() b/1
b/1
a/0 a/1
Működés:
- kimeneti szó n. betűje 1, ha a bemeneti szóban az első n betű között páratlan b szerepel
- 0 különben
Példa baabbab
Moore - automata
(A kimeneti jel csak a belső állapottól függ.)
N:=< A, V, W, d l, q0>, ahol: - A: belső állapotok véges, nem üres halmaza
- V: bemenő ábécé
- W: kimenő ábécé
- d átmenetfüggvény d:A V A
- l kimeneti függvény l: A W
- q0: kezdőállapot q0 A
Működés: a1.... ak V* bemeneti szóra
0., b0:=l(q0) 1. kimeneti jel meghatározása
1., q1:=d(q0,a1) új belső állapot meghatározása
b1:=l(q1) 2. kimeneti jel meghatározása
:
:
k., qk :=d(qk-1,ak)
bk :=l(qk)
Megjegyzés: Kimeneti szóban egy betűvel több van, mint a bemeneti szóban.
Jelölés: N(w w bemenő szóból átalakított kimeneti szó.
Megadás: - táblázattal
- gráffal
Példa N1:=< d l, q0>
d(q0,a) = q1
d(q0,b) = q2 l(q0) = 0
d(q1,a) = q1
d(q1,b) = q2 l(q1) = 1
d(q2,a) = q1
![]()
![]() d(q2,b)
= q2 l(q2)
= 0
d(q2,b)
= q2 l(q2)
= 0
Táblázattal:
|
d l |
a |
b |
|
q0 |
q1,0 |
q2,0 |
|
q1 |
q1,1 |
q2,1 |
|
q2 |
q1,0 |
q2,0 |
![]()
![]() Gráffal: a
Gráffal: a
![]()
![]() a q1,1
a q1,1
![]()
![]()
![]()
![]()
![]() q0,0 b
q0,0 b
![]() b a
b a
![]()
![]()
![]() q2,0
q2,0
b
Működés:
- Kimeneti szó első betűje 0
- Többi betűnél: bemenő a-t egyesre, b-t nullára cseréljük.
Definíció M:=<A, V, W, d l, q0> Mealy - automata
N:=<A', V, W, d l', q0'> Moore - automata
M és N ekvivalensek, ha minden w bemeneti szóra: bM(w) = N(w), ahol b:=l '(q0').
Tétel Tetszőleges Mealy-automatához létezik vele ekvivalens Moore-automata.
Tétel Tetszőleges Moore-automatához létezik vele ekvivalens Mealy-automata.
Tétel L V* reguláris nyelv. M Mealy-automata, V bemenő ábécével. Ekkor M(L) reguláris
Találat: 1983