Vektorok. Szakaszok a koordinatasíkon

Vektorok. Szakaszok a koordinátasíkon

I. Fogalmak

Vektor: irányított egyenes szakasz, melyet állása, iránya és hossza jellemez

ˇ   &nbs 313i87d p;   &nbs 313i87d p; Vektor állása azt mutatja, hogy melyik egyenesekkel párhuzamos → egy álláson belül két irány lehetséges

ˇ   &nbs 313i87d p;   &nbs 313i87d p; Vektor hossza: a vektor abszolút értéke |a|=a

ˇ   &nbs 313i87d p;   &nbs 313i87d p; Egy vektor megadható, ha ismerjük állását, irányát és hosszát

ˇ   &nbs 313i87d p;   &nbs 313i87d p; Jelölés: a vektor: aláhúzott kisbetű - a

Kezdő- és végpontja fölé tett nyíllal

Nyomtatásban vastagabb betűtípussal

ˇ   &nbs 313i87d p;   &nbs 313i87d p; Egységvektor abszolút értéke 1

ˇ   &nbs 313i87d p;   &nbs 313i87d p; Derékszögű koordinátarendszerben az x, y és z tengelyek pozitív irányba mutató egységvektor jelei rendre i, j, és k

Nullvektor: kezdő- és végpontja egybeesik

ˇ   &nbs 313i87d p;   &nbs 313i87d p; Abszolút értéke 0

ˇ   &nbs 313i87d p;   &nbs 313i87d p; Iránya tetszőleges

Egyenlő vektorok: nullvektortól különböző vektorok akkor és csak akkor egyenlők, ha irányuk és abszolút értékük megegyezik

Ellentett vektor: ugyanakkora nagyságú, de ellentétes irányú vektor

Helyvektor: derékszögű koordinátarendszerben a P(x;y) pont helyvektora az origóból a pontba mutató vektor

II.

1.   &nbs 313i87d p;   két vektor szöge

két egyállású vektor szöge 0°-os, ill. 180°-os, aszerint, hogy a vektorok egyirányúak vagy ellentétes irányúak

két nem egyállású vektor szögét úgy kapjuk meg, hogy azonos pontból indítjuk a vektorokat, s a keletkező kisebb szöget választjuk

2.   &nbs 313i87d p;   ha i az (1;0), j pedig a (0;1) pont helyvektora, akkor a sík bármely a vektora egyértelműen előállítható a = a₁i + a₂j alakban

(az i és j vektorok lineáris kombinációjaként)

III. Vektorműveletek

1.   &nbs 313i87d p;   vektorok összeadása

ha egy vektor ugyanazt az eltolást hozza létre, mint a-val és b-vel való eltolás egymásutánja, akkor ezt a vektort az a és b összegének nevezzük

jele: a+b

"paralelogramma módszer" (ha a vektorok nem egyállásúak)

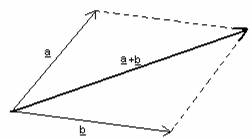két vektor összegét úgy kapom meg, hogy közös kezdőpontból felveszem a két vektort, majd e vektorok végpontjain át párhuzamost húzok a másik vektorral, s az így kapott paralelogramma közös pontjából a szemközti átlóvektort berajzolom

"láncmódszer"

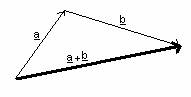két vektor összegét úgy kapom meg, hogy felveszem az egyik vektort, a végpontjából pedig a másikat. Ekkor az első vektor kezdőpontjából a másik vektor végpontjába mutató vektor az összegvektor

A láncmódszerrel több vektor is összeadható.

A vektorok összeadása kommutatív (felcserélhető: a+b=b+a)

és asszociatív (csoportosítható: (a+b)+c=a+(b+c))

Két vektor összegének koordinátái

a=a₁i + a₂j

b=b₁i + b₂j

a+b=(a₁+b₁)i + (a₂+b₂)j

Két ellentett vektor összege: nullvektor

2.   &nbs 313i87d p;   két vektor különbsége

ha c=a+b, akkor az a-t a c és b különbségének mondjuk

jele: c-b

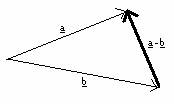
a és b különbségén értjük azt a vektort , amit úgy kapunk meg, hogy közös kezdőpontból felveszem a-t és b-t, majd végpontjaikat összekötöm, és a kisebbedő felé irányítom

↓

A vektorok esetén igaz, hogy c-a és a-c egymás ellentettje

két egyenlő vektor különbsége: nullvektor

két vektor különbségének koordinátái

a=a₁i + a₂j

b=b₁i + b₂j

a-b=(a₁-b₁)i + (a₂-b₂)j

két vektor különbségét a kivonandó vektor -1-gyel való szorzása után a vektorok összegére vezethetjük vissza

3.   &nbs 313i87d p;   vektor számszorosa

Az a λ-szorosán értjük azt a vektort, amelynek hossza az a hosszának | λ|-szorosa, iránya pedig az a irányával megegyező, ellentétes, vagy tetszőleges, attól függően, hogy λ>0; λ<0; λ=0

| λa|=a| λ|

minden vektor egyenlő egységvektorának és abszolút értékének szorzatával

vektor számszorosának koordinátái

a=a₁i + a₂j

λ valós szám

λa=(a₁ λ)i + (a₂ λ)j

érvényesek az alábbi azonosságok

αa + βa=(α + β)a

α(βa)=( )a

α(a+b)=αa + αb

4.   &nbs 313i87d p;   két vektor skaláris szorzata

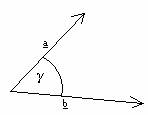Ha a és b által közbezárt szög γ, akkor az |a|*|b|*cosγ számot az a és b skaláris szorzatának nevezzük

Jele: a*b

↓

a*b=|a|*|b|*cosγ

ha két vektor hajlásszöge 90°, akkor a skaláris szorzatuk 0 (mert cos90°=0)

két egyállású és egyirányú vektor skaláris szorzata az abszolút értékek szorzatával egyenlő (mert cos0°=1)

kommutatív (a*b=b*a)

disztributív ((a+b)c=a*c + b*c)

de! nem asszociatív ((a+b)*c≠a(b*c))

skaláris szorzat koordinátákkal kifelezve

a=a₁i + a₂j

b=b₁i + b₂j

a*b=a₁*b₁ + a₂*b₂

tétel: két, koordinátákkal megadott vektor skaláris szorzata a megfelelő komponensek szorzatösszegével egyenlő

a*b=a₁*b₁ + a₂*b₂

bizonyítás:

a=a₁i + a₂j

b=b₁i + b₂j

a*b = (a₁i + a₂j)(b₁i + b₂j) = a₁*b₁i² + a₁*b2ij + a₂*b₁ij + a₂*b₂j² =

i²=1; j²=1

i és j hajlásszöge 90°

=a₁*b₁ + a₂*b₂ ↓

skaláris szorzatunk 0

5.   &nbs 313i87d p;   vektorok vektoriális szorzata

Az a és b vektoriális szorzata egy olyan c vektor, melynek

abszolút értéke a vektorokkal szerkesztett paralelogramma területének mértékszámával egyenlő

iránya mindkét vektorra merőleges

irányítása olyan, hogy a, b és c ilyen sorrendben jobbsodrású rendszert alkotnak ("jobbkéz-szabály")

jele: a x b

|c| = |a×b| = |a|*|b|*sinγ

Tétel: két nem nullvektor párhuzamossági feltétele: a×b

Biz.: a definícióból következik, mert sin0°=0

Tétel: ha két vektor merőleges egymásra, akkor a vektoriális szorzatuk abszolút értéke  |a×b| = |a|*|b|

Biz.: a definícióból következik, mert sin90°=1

tulajdonságai

nem kommutatív: a×b = -(a×b)

disztributív: a x (b+c) = (a x b) + (a x c)

IV.

1.   &nbs 313i87d p;   a vektor felbontása összetevőkre

egyértelmű vektorfelbontás tétele:

ha a v, az i és a j olyan, egy síkban lévő vektorok, hogy az i és j nem egyállású, akkor a v egyértelműen bontható fel két olyan vektor összegére, amelyek egyike az i-ral, másik a j-ral egyállású

v = v₁i + v₂j

Az i és a j merőleges egységvektorok egy bázisrendszert alkotnak. Ezek együtthatóit nevezzük koordinátáknak.

2.   &nbs 313i87d p; 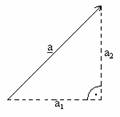  vektor hossza

|a| = √a₁² + a₂²

3.   &nbs 313i87d p;   a vektor 90°-os elforgatottja

Ha egy vektort 90°-kal elforgatunk, akkor a koordinátái felcserélődnek és az egyiknek az előjele megváltozik.

v(v₁;v₂)

+90°-os elforgatottja: (-v₂;v₁)

-90°-os elforgatottja: (v₂;-v₁)

4.   &nbs 313i87d p;   két vektor hajlásszöge

a*b = |a|*|b|cosγ

a*b = a₁*b₁ + a₂*b₂

↓

|a|*|b|cosγ = a₁*b₁ + a₂*b₂

Ha két vektor koordinátáival adott, akkor a hajlásszögük meghatározható.

V. Vektorok a koordinátasíkon

1.   &nbs 313i87d p;   szakasz felezőpontja koordinátái 2 végpontjának a megfelelő koordinátáinak az összegének a fele

Biz.:

Adott az A(a₁;a₂) és B(b₁;b₂) pontok által meghatározott szakasz.

Felezőpontja: F(x;y)

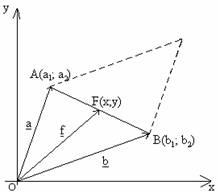
Ha az A, B és F pontok helyvektorai rendre a, b és f, akkor a vektorok összegezésének paralelogramma szabály alapján - felhasználva, hogy a paralelogramma átlói felezik egymást - adódik, hogy: f = (a+b)/2

Vektorok összegének koordinátáira vonatkozó összefüggések alapján koordinátákkal:

x = (a₁+b₁)/2 y = (a₂+b₂)/2

2.   &nbs 313i87d p;   szakaszt adott arányban osztó pont koordinátái

Adott az A(a₁;a₂) és B(b₁;b₂) pontok által meghatározott szakasz. R(x;y) pontjának koordinátáit keressük, amelyre igaz, hogy AR : RB = p : q.

Legyenek A, B, R pontok helyvektorai rendre a, b és r.

Mivel: AR / RB = p / q ezért

Ezt felhasználva:

r = a + = a + = a +

Így az R pont koordinátái:

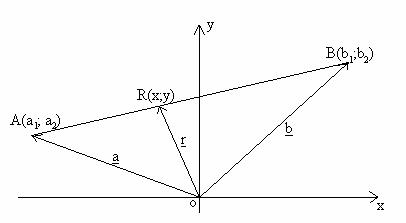
Szakasz harmadoló pontjának helyvektora:

A harmadoló ponttól számítva a szakasz közelebbi végpontjának helyvektorának 2/3-a + a szakasz távolabbi végpontjának 1/3-a.

VI. Alkalmazások

1.   &nbs 313i87d p;   Koszinusztétel vektoros bizonyítása

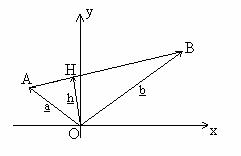
Az ABC háromszög oldalai legyenek AB = c; CB = a; CA = b

→ háromszögben: c = a - b

Négyzetre emelve: c² = a² + b² - 2ab

Skaláris szorzat definíciója alapján: c² = a² + b² - 2|a|*|b|cosγ

Mivel a vektorok skaláris négyzete egyenlő abszolút értékük négyzetével:

c² = a² + b² - 2abcosγ

2.   &nbs 313i87d p;   a háromszög súlypontjának koordinátái

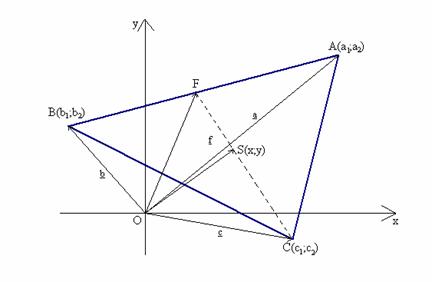
Legyenek az ABC háromszög A(a₁;a₂), B(b₁;b₂), C(c₁;c₂) csúcspontjainak helyvektorai rendre a, b és c

Ha F az AB szakasz felezőpontja, akkor az F pont f helyvektora

Ha a CF szakasz F-hez közelebbi S harmadoló pontjának helyvektora s, akkor

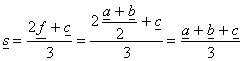
Mivel a fenti kifejezés független attól, hogy melyik oldal megfelelő felezőpontjából indulunk ki, ezért mindhárom súlyvonal a megfelelő csúcstól távolabbi harmadoló pontja ugyanaz az S pont. Ezzel bebizonyítottuk azt is, hogy a háromszög súlyvonalai egy pontban metszik egymást.