| kategória | ||||||||||
|
|
||||||||||
|
|
||
LINEÁRIS ALGEBRA
Vektorok
Vektor fogalma
Vannak olyan mennyiségek, melyeknek a nagysága a fontos (út, tömeg, munka, stb.). Ezek a skalár mennyiségek.
Vannak olyan mennyiségek, melyeknek a nagyságukon kívül az irányuk (irányítottságuk) is fontos (sebesség, erő, stb.). Új fogalom vektormennyi-ségek.
Irányított szakaszokat vektoroknak nevezünk.

A vektor ismert, ha ismerjük:
nagyságát: hosszát. 2 km
irányát: É-D
irányítottságát: D-ről É-ra mutat.
Jelölése: ![]() írásban (a
írásban (a
a nyomtatásban.
A v vektor hosszát a v vektor abszolút értékének nevezzük és │v│-vel jelöljük (v-vel, ha a szövegből kiderül).
Azt a vektort, melynek abszolút értéke 0, nullvektornak nevezzük és 0-val jelöljük.
Azt a vektort, melynek hossza egységnyi, egységvektornak nevezzük és ea val jelöljük (a írányú egységvektor).
Két vektor, a és b akkor egyenlő, ha van olyan párhuzamos eltolás amely-nél fedésbe hozhatók:
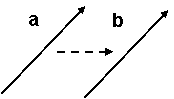

egyenlők nem egyenlők
Megfeleltetés a sík (tér) pontjai és a vektorok között:
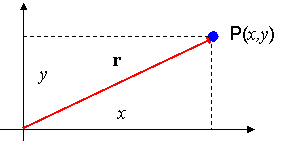 Egyértelmű
megfeleltetés van a sík pontjainak halmaza (R2) és a vektor között:
Egyértelmű
megfeleltetés van a sík pontjainak halmaza (R2) és a vektor között:
![]() egyenes
egyenes
![]() sík
sík
![]() tér
tér
Műveletek vektorokkal
Vektorok összeadása
Az a és a b vektorok összegén azt az a+b vektort értjük, amely az a kezdőpontjából a b végpontjába mutat.
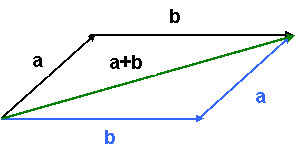
Az a és b szerepe felcserélhető
Paralellogramma szabály
Több vektorra is értelmezhető
Tulajdonságai: a+b=b+a kommutatív
(a+b)+c=a+(b+c) asszociatív
a+0=a nullvektor
a+(-a)=0 az ellentettje
Vektor szorzása skalárral
Adott a vektor és λ skalár szám (![]() )
szorzatán azt a vektort értjük, melynek hossza:
)
szorzatán azt a vektort értjük, melynek hossza: ![]()
iránya párhuzamos a-val
irányítottsága a előjelétől függ: ha + azonos
ha - ellentétes a-val.
![]()
![]() Ha >1 nyújtás
Ha >1 nyújtás
![]()
![]() <1, de >0 zsugorítás
<1, de >0 zsugorítás
![]()
![]() tükrözés
tükrözés
Bármely a vektor előállítható ![]() alakban, ahol az
alakban, ahol az ![]() az a
irányú egységvektor.
az a
irányú egységvektor.
Két vektor (a és b) akkor van egy
egyenesen, ha létezik egy ![]() amelyre a= b.
amelyre a= b.
Vektorok kivonása (különbsége)
Az a és a b vektorok különbségén azt az a-b vektort értjük, melyet hozzá-adva b-hez a-t kapunk.
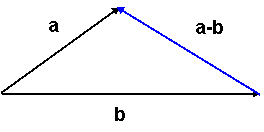 a-b ≠ b-a nem kommutatív
a-b ≠ b-a nem kommutatív
Vektorok lineáris kombinációja
Legyen ![]() és
és ![]() ,
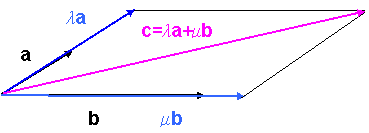
akkor a c= a b vektort az a és a b vektorok lineáris kombinációjának nevezzük.
,
akkor a c= a b vektort az a és a b vektorok lineáris kombinációjának nevezzük.
 kombináció:
az összeadás és a skalárral való szorzás kombinálása.
kombináció:
az összeadás és a skalárral való szorzás kombinálása.
lineáris: lineáris tér elemei (lsd.később).
Nézzük megfordítva is: mikor állítható elő egy c vektor adott a és b vektorok lineáris kombinációjaként?
Akkor, ha az a nem párhuzamos a b-vel. Ez azt jelenti, hogy
a b ahol
![]()
akkor és csak akkor, ha ![]() .
Ezen feltételnek eleget tevő vektorokat lineárisan független vektoroknak
nevezzük. Ellenkező esetben lineárisan összefüggők.
.
Ezen feltételnek eleget tevő vektorokat lineárisan független vektoroknak
nevezzük. Ellenkező esetben lineárisan összefüggők.
Bizonyítás: legyen
pl. α≠0. Ebben az esetben az előző ![]() alakba írható, azaz b párhuzamos a-val.
alakba írható, azaz b párhuzamos a-val.
Háromdimenziós vektoroknál a lineáris függetlenség feltétele:
a b + ![]() c akkor
és csak akkor, ha
c akkor
és csak akkor, ha ![]() .
.
Lineáris összefüggés esetén a három vektor egy síkban van.
Lineárisan független vektorok segítségével a (tér esetén három, a sík esetén kettő) bármelyik v vektora felírható, mint azok lineáris kombinációi. Ezeket a lineárisan független vektorokat bázisvektoroknak nevezzük.
Bármely három (sík esetén kettő) lineárisan független vektor lehet bázis-vektor. Célszerű azonban úgy megválasztani azokat, hogy
Ortonormált bázistér
Legyenek egymásra merőlegesek (ortogonálisak),
Legyenek egységvektorok (normáltak).
Az első választás a skalárszorzat kiszámítását egyszerűsíti, a második lehetővé teszi a vektorok koordinátákkal történő megadását.
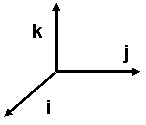
Az i, j, k az ortonormált bázisvektorok. Jobbsodrású rendszert alkotnak.
A v vektor felírása: v = xi yj zk
Koordinátákkal való megadás: v=(x;y;z
A koordinátákkal való felírás lényegesen megkönnyíti a műveletek elvégzését.
Műveletek koordinátákkal megadott vektorokkal
Legyen a=(a1 a2 a3 és b=(b1 b2 b3;), valamint ![]()
1. Összeadás:
a+b a1i a2j a3k b1i b2j b3k a1+b1)i+ a2+b2)j+ a3+b3)k,
mivel az összeadás asszociatív és disztributív. Két vektort úgy adunk össze (vonunk ki), hogy megfelelő koordinátáikat összeadjuk (kivonjuk).
Skalárral való szorzás
a a1i a2j a3k λa1)i+ λa2)j+ λa3)k
a koordinátákat meg kell szorozni.
3. Vektor szorzása vektorral
Skalár(is)
szorzat ![]()
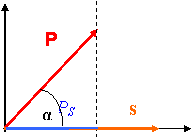
Fizikai példa a munka: ![]()
![]()
amit felírhatunk L=P∙s alakban és az erőnek valamint az útnak (valójában az elmozdulásnak), mint a két vektornak skalár(is) szorzatának nevezünk.
Az a és a b vektorok skalár(is) szorzatán az ![]() számot
értjük, ahol az
számot
értjük, ahol az ![]() a két vektor hajlásszöge.
a két vektor hajlásszöge.
![]() negatív
negatív
![]() pozitív
pozitív
![]() nulla.
nulla.
Két vektor skalárszorzata akkor és csak akkor 0, ha azok merőlegesek egymásra.
A skalárszorzat tulajdonságai:
a∙b=b∙a kommutatív
a∙(b+c)=a∙b+a∙c disztributív
a∙b∙c nincs értelme
A skalárszorzat kiszámítása
Először a bázisvektorok skalárszorzata: i∙i=j∙j=k∙k=1
i∙j=j∙k=k∙i=0
ebből:
a∙b=(a1i+a2j+a3k) ∙ (b1i+ b2j+b3k)= (a1∙b1)ii+(a1∙b2)ij+(a1∙b3)ik + +(a2∙b1)ji +(a2∙b2)jj+(a2∙b3)jk+(a3∙b1)ki +(a3∙b2)kj+(a3∙b3)kk
azaz:
a∙b
=a1∙b1+a2∙b2+a3∙b3=
![]()
Alkalmazásai:
A vektor hossza: ![]()
![]()
Egységvektor: 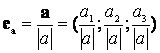
Két
vektor hajlásszöge: 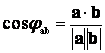
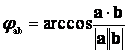
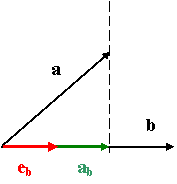 Vetület:
Vetület:
a
vetület hossza: 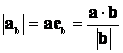
a
vetületvektor: 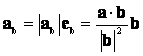
 Vektor(iális) szorzat
Vektor(iális) szorzat
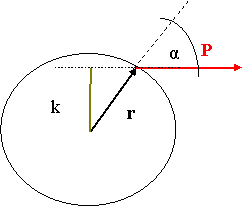
Fizikai példa a forgatónyomaték
![]()
az erő és karja vektorok:
![]()
A forgatónyomaték nagysága:
![]()
A forgatónyomaték azonban vektor! ![]() vektorszorzat
vektorszorzat
nagysága: ![]()
iránya: merőleges az r és a P síkjára
irányítottsága: r, P és ![]() jobbsodrású.
jobbsodrású.
Az a és a b vektorok axb vektoriális szorzatának nevezzük azt a vektort, amelynek:
nagysága: ![]()
iránya: merőleges az a és a b síkjára
irányítottsága: a,
b és ![]() jobbsodrású.
jobbsodrású.
Tulajdonságai: nem kommutatív: axb≠bxa (axb=-bxa )
nem asszociatív: ax(bxc)≠(axb)xc
disztributív: ax(b+c)=axb+axc
Két vektor vektoriális szorzata akkor és csak akkor nulla, ha a két vektor egymással párhuzamos.
A vektorszorzat kiszámítása
Először a bázisvektorok vektorszorzata: ixi=jxj=kxk=0
ixj=k, jxk=i, kxi=j
ixk=-j, jxi=-k, kxj=-i
Ezeknek a felhasználásával:
![]()
axb=(a1i+ a2j+ a3k) x (b1i+ b2j+b3k)= (a1∙b1)i x i+(a1∙b2)i x j+(a1∙b3)i x k + +(a2∙b1)j x i +(a2∙b2)j x j+(a2∙b3)j x k+(a3∙b1)k x i +(a3∙b2)k x j+(a3∙b3)k x k=
azaz:
![]()
![]()
elég bonyolult megjegyezni. Egyszerűbben:
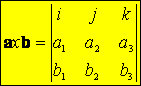
determináns első sor szerinti kifejtése.
Vegyes szorzat:
Az a, b és a c vektorok vegyes szorzata (axb)c=abc
Jelentése a három vektor által kifeszített paralellepipedon térfogata
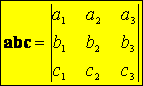
Értéke zérus, ha a három vektor egy síkban van ← lineárisan összefüggők.
2. Mátrixok
Készítsünk egy táblázatot
|
|
jeles |
jó |
közepes |
elégséges |
elégtelen |
|
Matematika |
|
|
|
|
|
|
Villamosságtan |
|
|
|
|
|
|
Közgazdaságtan |
|
|
|
|
|
|
Angol |
|
|
|
|
|
Hagyjuk el a keretet:
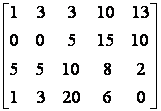 Mátrix
Mátrix
Műveletek végezhetők velük.
Mátrixnak nevezünk bármilye nxm számadatot az alábbi téglalap alakú elrendezésben:

Az n a sorok, m az oszlopok száma, ha n=m négyzetes mátrix.
![]() A mátrix főátlója.
A mátrix főátlója.
Írásban általában: ![]() jelöljük.
jelöljük.
A mátrix transzponáltja: ha oszlopait és sorait felcseréljük (tükrözzük a főátlóra):
![]()
A minormátrix: elhagyjuk a mátrix néhány sorát, illetve oszlopát.
![]()
elhagytuk a 2 és az 5 sort, illetve az 1 és a 3 oszlopot.
Műveletek mátrixokkal
Mátrixok egyenlősége: 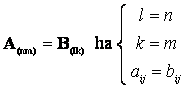
Mátrixok összeadása: ![]()
![]()
kommutatív és asszociatív művelet.
Mátrix szorzása skalárral ![]()
Kommutatív, asszociatív és disztributív művelet.
Mátrix szorzása mátrixszal:
A és B mátrix szorzata C=A∙B akkor értelmezhető, ha A-nak ugyanannyi oszlopa van, mint ahány sora B-nek, azaz:
![]()
ebben az esetbe a C mátrix cij eleme az alábbi lesz:
![]()
elég nehéz megjegyezni: Falk módszer:
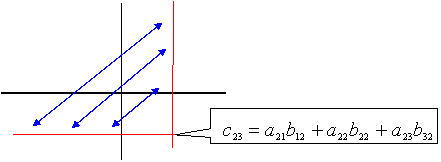
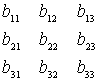 B
B
A 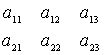 C
C
A szorzás: nem
kommutatív ![]() lehet, hogy el sem végezhető
lehet, hogy el sem végezhető
asszociatív ![]()
disztributív ![]()
Négyzetes mátrixnál: ![]()
![]()
Előfordulhat, hogy az eredmény úgy lesz 0 mátrix, hogy a szorzandók közül egyik sem az.
Sor- és oszlopvektorok
Lehetnek egysoros, vagy egyoszlopos mátrixok:
Egyoszlopos 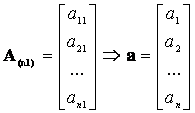 oszlopvektor
oszlopvektor
Egysoros: ![]() ,
mivel az oszlopvektor transzponáltja.
,
mivel az oszlopvektor transzponáltja.
Sor- és oszlopvektorok szorzása: A mátrixszorzás szabályai szerint csak sorvektort lehet oszlopvektorral, vagy oszlopvektort sorvektorral össze-szorozni, továbbá (n=m).
Sorvektor szorzása oszlopvektorral:
![]()
![]() skalárszorzat, skalár.
skalárszorzat, skalár.
Oszlopvektor szorzása sorvektorral:
 diadikus szorzat, mátrix.
diadikus szorzat, mátrix.
Speciális mátrixok
1. Zérusmátrix: 
2. Egységmátrix: 
3. Egységvektorok :
oszlop: 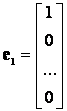 ,
, 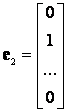 ,...
,...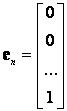
sor: ![]() ,
, ![]() ,..
,..![]()
Közülük is a legfontosabbak a 3x3-as mátrixok és 3 dimenziós vektorok ( a háromdimenziós tér elemei).
3. Determinánsok
n-edrendű determinánsnak nevezzük az alábbi nxn elemből álló

alakú táblázatot, amelynek a következő értéket tulajdonítunk:
=![]() ,
,
ahol az A1k az a1k elemhez tartozó előjeles aldetemináns, amelyet úgy kapunk meg, hogy az első sort és a k-adik oszlopot elhagyjuk és maradékot megszorozzuk (-1)k+1 -val.
Az aldetermináns (n-1)x(n-1) és determináns lesz, azaz eggyel kisebb. Erre szintén alkalmazzuk a fenti definíciót egészen 1x1- esig, ami már egy valós szám, ezzel már értelmezve van a szorzás. Végül egy valós számot kapunk, amely a determináns értéke. Rekurzív definíció.
A gyakorlatban csak a 2x2-esig megyünk el, mivel annak az értéke:
![]()
![]() =ad-bc
=ad-bc
Ezt a determináns első sora szerinti kifejtésnek nevezzük.
Példa
A determináns tulajdonságai:
A determinánst bármely sora, vagy oszlopa szerint kifejtve ugyanazt kapjuk. Az előjelek a sakktábla szabály szerint:
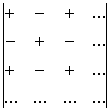
A determináns értéke nem változik, ha sorait és oszlopait felcseréljük (tükrözzük).
Ha a determináns két sorát (oszlopát) felcseréljük értéke (-1)-el szorzódik:
a. Két szomszédos (sakktábla szabályból)
b. Bármely kettő páratlan számú szomszéd cserékre vissza-vezethető).
Ha egy determináns két sora (oszlopa) azonos, értéke 0 (bizonyítás felcseréléssel).
Ha valamelyik sora (oszlopa) 0, akkor értéke is 0 (ez szerint fejtjük ki. Következmény: érdemes azon sora (oszlopa) szerint kifejteni, melyben sok 0 van.
Ha egy determináns főátlója alatt (felett) csupa 0 van, akkor értéke a főátlóban lévő elemek szorzata.
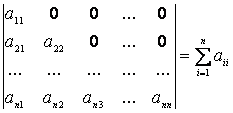
Ha a determináns valamelyik sorában (oszlopában) minden elem két elem összegére (vagy különbségére) bontható, akkor a determináns is két determináns összegére:

Ha valamelyik sor (oszlop) valamennyi
elemét ![]() -val
meg-szorozzuk, akkor a determináns értéke is szorzódik -val.
-val
meg-szorozzuk, akkor a determináns értéke is szorzódik -val.
Ha a determináns valamelyik sora (oszlopa) a másik többszöröse, akkor értéke 0 (kiemelem a többszöröst, sor (oszlop) meg fog egyezni).
A determináns értéke nem változik, ha valamelyik sorához (oszlo-pához) a másik sorának (oszlopának) valahányszorosát hozzáadjuk. Következmény: Így lehet valamelyik sorból (oszlopból) egy elem kivételével csupa 0-t csinálni és ezt az 5 szerint könnyű kifejteni.
Négyzetes mátrix determinánsa
A négyzetes mátrix, ha n=m , azaz sorainak és oszlopainak a száma megegyezik.
A négyzetes mátrix rendje n (sorainak, illetve oszlopainak a száma).
 mátrix
determinánsán a
mátrix
determinánsán a 
mennyiséget értjük:
Ha ![]() a mátrix reguláris
a mátrix reguláris
Ha ![]() a mátrix szinguláris
a mátrix szinguláris
A mátrix rangja
Az A mátrix ρ(A) rangján a legnagyobb reguláris minormátrix (négyzetes lesz) rendjét értjük.
Példa: 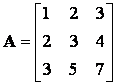 rangja, ρ(A)=2, mivel detA=0,
de
rangja, ρ(A)=2, mivel detA=0,
de 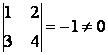 .
.
A rangnak fontos szerepe van az alkalmazásban.
A négyzetes mátrix adjungáltja
A négyzetes mátrix adjungáltja az a mátrix
 , ahol az Aij az a mátrix aij elemeihez
, ahol az Aij az a mátrix aij elemeihez
tartozó aldetermináns (transzponálva van!).
Vagyis a meghatározási metódus:
![]()
Példa:
Bebizonyítható: ![]()
A négyzetes mátrix inverze
Az A négyzetes mátrix inverze az a mátrix, A-1, amelyre igaz, hogy A-1A=E.
Kiszámítása az előzőből: ![]()
![]()
![]() ebből:
ebből: 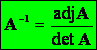
akkor létezik, ha ![]() azaz az A mátrix
reguláris. (Az inverz megfelel a skalárnál a reciproknak. 0-nak nincs
reciproka).
azaz az A mátrix
reguláris. (Az inverz megfelel a skalárnál a reciproknak. 0-nak nincs
reciproka).
Azonosságok: ![]()
![]() és
és ![]()
Példa:
4. Lineáris tér
Több olyan fogalommal találkoztunk (valós számok, vektorok, mátrixok), amelyeknél értelmezve van az összeadás és a szorzás művelete az adott (valós számoknál felsorolt) tulajdonságokkal. Ezek a mennyiségek lineá-ris teret alkotnak, amit L-lel jelölünk (Ln n-dimenziós lineáris tér).
A matematikának a lineáris tér elemeivel foglalkozó ága a lineáris algebra
A lineáris tér elemeit vektoroknak (n-dimenziós) nevezzük, még ha valóban nem is azok, ugyanis:
a valós szám (skalár) egydimenziós vektornak,
![]()
a mátrix m darab n dimenziós oszlopvektornak tekinthető.
![]() , ahol
, ahol 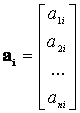
n-dimenziós vektorok
Nemcsak három (tér) hanem akárhány komponensű (n>3) vektorokat is definiálhatunk:
![]()
ugyanaz érvényes rájuk, mint a háromdimenziósokra, ugyanúgy lehet velük műveleteket végezni (kivéve a vektorszorzást). →szám n-esek →n-dimen-ziós lineáris tér (Ln
Lineáris függetlenség
Legyenek xi vektorok (i=1; 2;..n) a Ln lineáris
tér elemei (![]() )
és αi valós
számok (
)
és αi valós
számok (![]() )
akkor az
)
akkor az
![]()
mennyiséget az ![]() vektorok lineáris kombinációjának nevezzük.
Amennyiben
vektorok lineáris kombinációjának nevezzük.
Amennyiben
![]() ,
,
akkor és csak akkor,
ha αi =0, ebben az
esetben az ![]() vektorokat lineárisan független vektoroknak
nevezzük. Ellenkező esetben lineárisan
összefüggők. Ekkor xi kifejezhető
a többi lineáris kombinációjaként.
vektorokat lineárisan független vektoroknak
nevezzük. Ellenkező esetben lineárisan
összefüggők. Ekkor xi kifejezhető
a többi lineáris kombinációjaként.
Bázisvektorok
Amennyiben b1, b2 ,.. bn vektorokat lineárisan független vektorok, azaz:
![]() ,
,
akkor és csak akkor igaz, ha![]() .
Ebben az esetben a b1, b2
,.. bn vektorok segítségével az Ln tér bármelyik a
vektora felírható, mint azok lineáris kombinációi:
.
Ebben az esetben a b1, b2
,.. bn vektorok segítségével az Ln tér bármelyik a
vektora felírható, mint azok lineáris kombinációi:
![]() , ahol
, ahol ![]() .
.
Ezeket a b1, b2 ,.. bn vektorokat bázisvektoroknak nevezzük. Bármely n számú lineárisan független vektor lehet bázisvektor.
Célszerű azonban: Egymásra merőleges ortogonális (skalárszorzat).
Egységvektor normált (koordináták).
Az így megválasztott bázisteret ortonormált bázistérnek nevezzük.
Három dimenzióban: 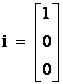
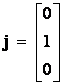 és
és 
n-dimenzióban: 
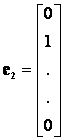 ....
.... 
Vektor: ![]()
![]()
ahol az a1, a2, és a3 illetve a1, a2, .. an az a vektor koordinátái az ortonormált bázistérben. Sok esetben célszerű azonban nem ortonormált bázisteret választani, például b1, b2 ,.. bn (pl. kristálytan, kristályok leírása). Ekkor az a vektor koordinátái ebben a bázistérben:
![]()
különbözni fognak az előző bázistérben kapottaktól.
Lineáris transzformációk
Az L lineáris térnek önmagában való lineáris leképezését lineáris transz-formációnak nevezzük.
Lineáris leképezés:
lineáris leképezés, ha ![]() és
és ![]() ,
akkor
,
akkor
![]()
![]()
és ![]() .
.
Hogyan is néz ki ez a leképezés?
Legyen a lineáris tér két vektora x x1 x2 xn ) és y y1 y2 yn ) továbbá tételezzük fel, hogy a két vektor koordinátái között a következő össze-függések vannak:

azaz:
![]() , ahol az
, ahol az  mátrix a lineáris
mátrix a lineáris
transzformáció mátrixa, amivel az x vektort (a lineáris tér egy elemét) leképezzük az y vektorba ( a lineáris tér egy másik elemébe):
Inverz transzformáció:
![]()
![]() a leképezés megfordítása.
a leképezés megfordítása.
Speciális leképezések:
Az egységmátrix a vektort önmagába viszi át
![]()
Nyújtás:
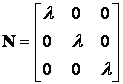 , ugyanis:
, ugyanis: 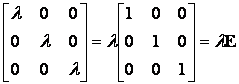
Tükrözés az xy síkra:
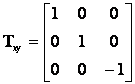
Forgatás a z tengely körül, φ szöggel:
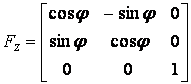
5. Lineáris egyenletrendszerek
Az

egyenletek halmazát lineáris egyenletrendszernek nevezzük, m egyenlet-ből és n ismeretlenből állnak.
![]() , az együtthatómátrix:
, az együtthatómátrix:

az ismeretlenvektor: 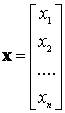 , a zavaróvektor:
, a zavaróvektor: 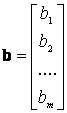
Az ismeretlenek (n) és az egyenletek (m) száma nem szükségszerűen azonos.
Független egyenlet az, amely nem következik a többiből, azaz nem állítható elő azok lineáris kombinációjaként. Ellenkező esetben nem független (azaz az egyenletrendszer lineárisan összefüggő).
Példa:
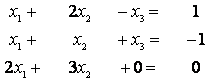
A harmadik egyenlet az első kettő összege, tehát nem független, így nem jelent új információt, tehát elhagyható. Ennélfogva az ismeretlenek száma n=3, a (független) egyenletek száma m* m*-gal jelöljük a független egyenletek számát, m*≤m (természetesen a harmadik helyett az első is elhagyható, mivel az a harmadik és a második különbsége, vagy a második, mert az pedig a harmadik és az első különbsége, azaz a lineáris kombináció bármelyik tagja).
Ha n>m*, akkor alulhatározott, néhány ismeretlen (n-m* ) szabadon megválasztható.
Ha n=m* , akkor határozott, n határozott gyök van.
Ha n<m*, akkor túlhatározott, nincs megoldás.
Összefoglalva: legyen a lineáris egyenletrendszernek az
![]() együtthatómátrixa és vezessük be a
együtthatómátrixa és vezessük be a
![]() bővített
mátrixot.
bővített
mátrixot.
A lineáris egyenletrendszer akkor és csak akkor oldható meg, ha a B bővített mátrix rangja megegyezik az A mátrix rangjával (bizonyítás a könyvben).
Homogén és inhomogén egyeletrendszerek:
![]() inhomogén
inhomogén
![]() homogén
homogén
Inhomogén egyenletrendszerek megoldása, Cramer-szabály
Az egyszerűség kedvéért tekintsük n=m-es egyenletrendszert (ha n>m, akkor hasonló lesz a megoldási eljárás a homogénhez). Ebben az esetben az i-edik gyök:
![]() , ahol a
, ahol a ![]() bővített
bővített
mátrixot úgy kapjuk, hogy az A együtthatómátrix i-edik oszlopa helyére beírjuk a b vektort. A módszer Cramer-szabályként ismert.
Példa:
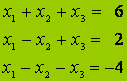

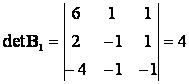
![]()
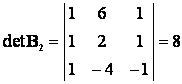
![]()

![]()
Homogén egyenletrendszerek megoldása
![]()
Triviális megoldás, x=0, akkor van, ha det A≠0 (lásd Cramer-szabály).
Nemtriviális megoldás akkor van, ha det A=0 . Ekkor viszont az egyenlet-rendszer lineárisan összefüggő, a nem független egyenletek (n-n*) elhagy-hatók, ennek megfelelően n-n*) ismeretlen szabadon megválasztható.
Példa:
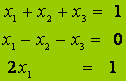 A harmadik a másik kettő
összege, így elhagyható.
A harmadik a másik kettő
összege, így elhagyható.
Melyik ismeretlen választható meg szabadon?
1. legyen x3=t ![]()


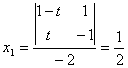

![]()
2. legyen x1=t ![]()

 x1 nem válaszható meg szabadon!
x1 nem válaszható meg szabadon!
Csak az(ok) az ismeretlenek választhatók meg szabadon, amelyeknél az átvitel után az együttható determináns nem nulla!
6. Bázistranszformációk
Az egyik bázisról való áttérést a másik bázisra, a bázisvektorok kicserélését, bázistranszformációnak nevezzük.
Elemi bázistranszformációk
A bázistranszformációk legegyszerűbb esete, amikor az adott bázisnak egy lépésben csak egy bázisvektorát cseréljük ki.
Legyenek a tér bázisvektorai : b1, b2 ,.. bn
Annak feltétele, hogy a bi bázisvektort kicserélhessük a tér egy adott b vektorával az, hogy
![]()
vektornak βi koordinátája ne legyen 0
Legyen a tér egy vektora: ![]()
Nézzük meg, hogyan alakulnak a vektor koordinátái, ha ![]() .
Kifejezve
.
Kifejezve ![]() vektort:
vektort:
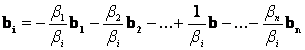 .
.
Behelyettesítve a vektor koordinátáiba, átrendezve:
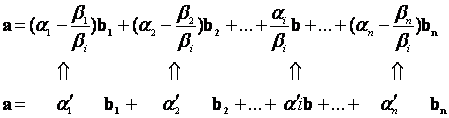
az új koordináták. Elég bonyolult kiszámolni.
Egyszerűsítés! A b vektor koordinátái a b1, b2,...b..bn bázistérben
(0; 0;..1;.0), azaz egységvektor lesz. Ezt
úgy kapom meg, hogy a b vektor koordinátáit végigosztom βi-vel,
ekkor az i-edik koordinátára 1-et
kapok és ennek β1-szeresét
kivonjuk az első (0 lesz), β2-szeresét a második
koordinátájából és így tovább. Ha ugyanezeket megcsináljuk (ugyanazt a
transzformációt) az a vektor
koordinátáira is, akkor könnyű belátni, hogy pont az ![]() koordinátákat kapjuk.
koordinátákat kapjuk.
Példa: a=(α1;
α 2; α3) ortonormált e , e2, e3 bázistérben. Cseréljük ki
az ![]() vektorra, akkor az a vektor koordinátái α'1, α'2, α'3
:
vektorra, akkor az a vektor koordinátái α'1, α'2, α'3
:
A következő táblázatot használhatjuk
|
|
b |
e2 |
e3 |
GENERÁLÓ ELEM |
e1
e2
e3
b
![]()
e2
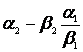
e3
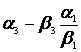
Példa: a=(1;2;3) ortonormált e , e2, e3 bázistérben. Cseréljük ki
az ![]() vektorra, akkor
vektorra, akkor
|
|
b |
e2 |
e3 |
A GENERÁLÓ ELEM |
e1
e2
e3
b
![]()
e2
![]()
e3
Kicserélhetjük az ![]() -ra
is és így tovább. Ez kétféleképpen oldható meg:
-ra
is és így tovább. Ez kétféleképpen oldható meg:
1. a c-t az ![]() cserét
követően vonjuk be a bázistranszformációba. Ez azt jelenti, hogy a c a b e2,
e3 bázistérben van már értelmezve. Legyen c(1;3;2)
cserét
követően vonjuk be a bázistranszformációba. Ez azt jelenti, hogy a c a b e2,
e3 bázistérben van már értelmezve. Legyen c(1;3;2)
|
|
b |
c |
e3 |
A GENERÁLÓ ELEM |
b
![]()
e2
![]()
e3
b
c
![]()
e3
2. a c-t az e1, e2,
e3 bázistérben van értelmezve, mint az a vektor. Ebben az esetben már a ![]() cserébe
is be kell vonni, azaz ebben az esetben az is transzformálódik, hasonlóképpen,
mint az a.
cserébe
is be kell vonni, azaz ebben az esetben az is transzformálódik, hasonlóképpen,
mint az a.
|
|
b |
c |
e3 |
A GENERÁLÓ ELEM |
e1
e2
e3
b
![]()
![]()
e2
![]()
![]() A GENERÁLÓ ELEM
A GENERÁLÓ ELEM![]()
e3
b
![]()
c
![]()
e3
![]()
A két eredmény
különbözik egymástól! És így tovább, az ![]() -re,
teljes bázistranszformáció.
-re,
teljes bázistranszformáció.
Alkalmazásai: Lineáris egyenletrendszer megoldása,
Mátrix rangjának meghatározása,
Mátrix inverzének meghatározása,
Determináns értékének a kiszámítása.
Lineáris egyenletrendszer megoldása
A megoldás elve:
![]()
Példa:

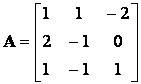
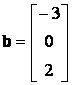
Megoldás:
|
Bázis |
x1 |
x2 |
x3 |
b |
|
e1 |
|
|
|
|
|
e2 |
|
|
|
|
|
e3 |
|
|
|
|
|
x1 |
|
|
|
|
|
e2 |
|
|
|
|
|
e3 |
|
|
|
|
|
x1 |
|
|
|
|
|
x2 |
|
|
|
|
|
e3 |
|
|
|
|
|
x1 |
|
|
|
|
|
x2 |
|
|
|
|
|
x3 |
|
|
|
|
azaz 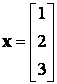
|
Bázis |
x1 |
x2 |
x3 |
b |
|
e1 |
|
|
|
|
|
e2 |
|
|
|
|
|
e3 |
|
|
|
|
|
x1 |
|
|
|
|
|
e2 |
|
|
|
|
|
e3 |
|
|
|
|
|
x1 |
|
|
|
|
|
x2 |
|
|
|
|
|
e3 |
|
|
|
|
|
x1 |
|
|
|
|
|
x2 |
|
|
|
|
|
x3 |
|
|
|
t |
A harmadik egyenlet elhagyható.
Az x2 vagy az x3 választható meg szabadon. Válasszuk meg az x3-t,
x3=t.
azaz: ![]()
![]()
![]()
Mátrix rangjának meghatározása
A megoldás elve:
A mátrix rangja a legnagyobb reguláris minormátrix (négyzetes, melynek determinánsa nem zérus) nagysága (sorainak, vagy oszlopainak, ami ugyanezt jelenti, a főátlóban lévő elemeinek száma).
Mivel azon determinánsok értéke, melynek csak a főátlójukban tartalmaz-nak 0-tól különböző elemeket, ezen elemek szorzata, így az ilyen mátrix rangja a főátlóban lévő 0-tól különböző elemek számával egyezik meg. Feladat olyan bázistranszformáció, amely ilye (egységmátrix) eredményez (ls az előzőt).
Példa:
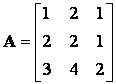 mátrix rangja, ρ ?
mátrix rangja, ρ ?
Megoldás:
|
Bázis |
a1 |
a2 |
a3 |
|
e1 |
|
|
|
|
e2 |
|
|
|
|
e3 |
|
|
|
a1
e2
e3
a1
a2
e3
Mátrix inverzének a meghatározása
A megoldás elve:
Skalár esetén: 
Mátrix esetén: 
Példa:
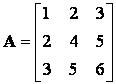 mátrix inverzének,
mátrix inverzének, ![]() -nak
a meghatározása
-nak
a meghatározása
Megoldás:
|
Bázis |
a1 |
a2 |
a3 |
e1 |
e2 |
e3 |
|
e1 |
|
|
|
|
|
|
|
e2 |
|
|
|
|
|
|
|
e3 |
|
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
e2 |
|
|
|
|
|
|
|
e3 |
|
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
e2 |
|
|
|
|
|
|
|
a3 |
|
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
a3 |
|
|
|
|
|
|
azaz 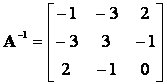
Determináns értékének a meghatározása
A megoldás elve:
A determináns valamelyik sorát elosztjuk egy számmal, akkor értéke is ennyivel osztódik. Azaz, ha ily módon a determináns elé kiemelünk egy számot, akkor a szorzat értéke nem változik. Továbbá, ha a determináns egyik sorához hozzáadjuk másik sorának többszörösét, szintén nem változik meg az értéke. Amennyiben a determináns főátlójában lévő elemek 1, a többi 0, akkor ennek a determinánsnak az értéke 1. Bázistranszformációval ezt előállítva, a determináns értéke a kiemelt elemek (generálóelemek) szorzata lesz.
Példa:

Megoldás:
|
Bázis |
a1 |
a2 |
a3 |
|
e1 |
|
|
|
|
e2 |
|
|
|
|
e3 |
|
|
|
|
a1 |
|
|
|
|
e2 |
|
|
|
|
e3 |
|
|
|
|
a1 |
|
|
|
|
a2 |
|
|
|
|
e3 |
|
|
|

A determináns értéke = -1
Tovább már nem is kell folytatni!
Találat: 5228