A MESTERSÉGES INTELLIGENCIA MÓDSZEREI A PROGRAMOZHATÓ AUTOMATÁKBAN

A MESTERSÉGES INTELLIGENCIA MÓDSZEREI A PROGRAMOZHATÓ AUTOMATÁKBAN

Az eddig ismertetett irányítástechnikai eszközök és módszerek közös jellemzője, hogy az

ember által ismert, rendszerint matematikai úton definiált irányítási algoritmusokat valósít-

ják meg, amelyek a rendszer matematikai modelljén alapulnak.

Ha a jelenlegi automatákat az ember irányító tevék 434j96e enységével összehasonlítjuk, azt

tapasztaljuk, hogy az ember számos olyan irányítási, döntési funkcióval rendelkezik, ame-

lyek a mai technikai szinten igen nehezen, vagy egyáltalán nem valósíthatók meg. Ilyenek

például az autóvezetés, a beszédfelismerés, a képfelismerés, a tanulással kombinált irányítás,

a tapasztalatokon alapuló döntések stb.

Az emberhez hasonló döntési, irányítási funkciók a mesterséges intelligencia mód-

szereinek irányítástechnikai alkalmazásával lehetségesek.

A mesterséges intelligencia (Artificial Intelligence, AI) módszereinek elemei:

− fuzzy módszerek;

− neurális hálózatok;

− genetikus algoritmusok;

− szakértői rendszerek;

− hibrid (vegyes) rendszerek.

Az intelligens irányítás (Intelligent Control, IC) fogalomköre négy tudomány terület-

re épül (7.1. ábra): irányításelmélet, számítástudomány, operációkutatás és mesterséges in-

telligencia módszerei

7.1. ábra. Az intelligens irányítás fogalma

Napjainkban a mesterséges intelligencia irányítástechnikai alkalmazása jó néhány te-

rületen mindennapossá vált (ABS fékrendszer, kamerafókuszálás stb.). Egyes PLC-, ill.

DCS-gyártó cégek a mesterséges intelligencia felhasználásához hardver- és szoftvermodulo-

kat forgalmaznak.

Az irányítástechnika területén inkább a fuzzy jellegű irányítás terjedt el, de vannak

tanuló típusú, modellbecslés alapján működő neurális automaták, sőt vegyes (neuro-fuzzy)

struktúrák is. A mesterséges intelligencia módszereinek alkalmazása a nem műszaki terüle-

teken (pl. orvostudomány, közgazdaságtan, szociológia) is jelentős.

7.1. Fuzzy jellegű irányítás

Az irányítási folyamatok egy részében (diszkrét technológiák) a lejátszódó folyamatok irá-

nyítása a Boole algebra módszereivel megfelelően leírható és a vezérléstechnika eszközeivel

megoldható.

Folyamatos technológiák irányításánál a folyamat szabályozása a cél. Ilyen esetben a

klasszikus szabályozáselmélet szükséges a tervezéshez. A szabályozástechnikai feladat konk-

rét megoldásához meg kell alkotni a rendszer pontos matematikai modelljét (pl. differenciál-

egyenlet, állapotegyenlet), amire a szabályozáselmélet módszerei alkalmazhatók.

Ez a módszer a gyakorlatban akkor használható, ha nem túl bonyolult a rendszer,

nincs túl sok be/kimenet, lineáris rendszerként értelmezhető, ill. a matematikai modell is-

mert.

A klasszikus szabályozástechnikai módszerek alkalmazásának a kulcsa a modellalko-

tás precízsége, azaz a modell mennyire pontosan írja le a tényleges rendszert. Ehhez ún.

mennyiségi modellezésre (quantitative modelling, kvantitatív modellezés) van szükség.

Az irányítási feladatok jelentős része a klasszikus szabályozástechnika módszereivel

csak körülményesen, ill. új módszerekkel oldható meg, ha a feladat túl bonyolult, vagy a

matematikai modell nem ismert, vagy a modell nem lineáris stb. Ilyen feladatok az autóveze-

tés, az ABS fékrendszer, a videokamera képélességének szabályozása, mosógép szabályozá-

sa a ruha szennyezettségtől függően stb.

Az ember a felsorolt irányítási tevékenységet viszonylag könnyedén megoldja anél-

kül, hogy egzakt matematikai modellt (kvantitatív modellt) használna. Ugyanis az ember

nem mennyiségi, hanem minőségi modellt (qualitative modell - kvalitatív modell) alkalmaz

az irányítási, döntési tevékenységének valamennyi területén.

A mennyiségi, ill. minőségi modellezés jelentőségét szemlélteti, hogy a fejezet szer-

zőjének irányításával került kidolgozásra a TEMPUS MODIFY projekt keretében számos

nyugati és hazai egyetem bevonásával a System Modelling angol nyelvű oktatási anyag a

PHARE program támogatásával [6].

A döntési folyamatokban a minőségi modellt használjuk, amely a lejátszódó folyamat

minősítésén alapul (pl. a hőmérséklet hideg, langyos, meleg, forró), ezért ezt a szabályozást

minősítő szabályozásnak nevezzük. A minősítő szabályozástechnika minőségükkel (pl. kicsi,

közepes, nagy, igen nagy) jellemzett változókon alapul. A milyenségükkel adott be- és ki-

meneti változók között feltételeket tartalmazó szabályokat alkot és így végzi el a szabályo-

zást, ezért gyakran szabály alapú (szabály bázisú, rule based) rendszernek nevezik és a tudás

alapú rendszerek közé sorolják.

Napjainkban a legelterjedtebb tudás alapú szabályozás a fuzzy (minősítő) szabályo-

zás. A fuzzy irányítók szabály alapú rendszerek, ahol a fuzzy halmazok határozzák meg az

irányító be- és kimenőjeleinek minőségi értékeit. A minőségi értékek többnyire nyelvi kifeje-

zések (nyelvi változók, linguistic variables), pl. kicsi, közepes, nagy, amelyek fuzzy halma-

zokkal kifejezhetők. A fuzzy logikával a szakértői tudás nyelvi változókkal könnyen imple-

mentálható és számítógépi algoritmussá formálható.

A fuzzy logika kidolgozása Lofti Zadeh nevéhez fűződik (1965). Az első fuzzy típu-

sú szabályozót Mamdani a nem lineáris gőzgép automatizálására fejlesztette és alkalmazta.

7.2. A fuzzy logika alapjai

7.2.1. Fuzzy halmazok

A halmazokat a körvonaluk tulajdonsága alapján feloszthatjuk crisp halmazra (éles, határo-

zott körvonalú) és fuzzy halmazra (életlen körvonalú).

Egy tetszőleges crisp halmaz a következő három módon adható meg [5]:

− ha a halmaz véges, akkor elemei felsorolásával pl.        A =

− az elemeire teljesülő szabállyal pl. B =

ha x A

− a halmaz karakterisztikus függvényével pl. X_A(x) = 

ha x A

A crisp halmazok karakterisztikus függvénye minden alaphalmazbeli elemhez 0-át

vagy 1-et rendel.

A fuzzy halmaz karakterisztikus függvénye az alaphalmaz minden eleméhez valamely

rögzített tartományból, amely általában a [0, 1] intervallum, rendel értéket. Ezen érték nagy-

sága a halmazbeli tagság értékével arányos. Az ilyen függvényt tagsági függvénynek

(membership function), az általa definiált halmazt fuzzy halmaznak nevezzük.

A fuzzy halmazt

jelöléssel fejezhetjük ki.

A

: X →

ill. A : X →

A fuzzy halmazokkal a bizonytalan határú természetes nyelvi fogalmak reprezentálha-

tók. A fuzzy halmaz és tagsági függvény fogalmát egy biológiai, ill. egy technikai példával

szemléltetjük.

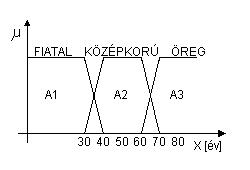
Az első példában három trapéz alakú halmazzal modellezzük az emberek életkorára

vonatkozó    fiatal, középkorú és öreg fogalmakat (7.2. ábra). A három fuzzy halmaz tagsági

függvényei a [30, 80] intervallumon követhetők:

ha x 30

<    <

A₁

x /10,

ha 30     x 40

ha x     40

ha x     30 vagy x 70

<    <

A₂= 

x 30 /10,

ha 30    x 40

≤

ha 40     x 60

<    <

x /10,

ha 60     x 70

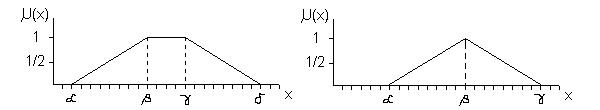
ha x 60

< <

A₃

 x   60 /10,

ha 60    x 70

ha x 70

7.2. ábra. Fiatal, középkorú, öreg fuzzy halmazok

A fuzzy halmazt és a tagsági függvényt értelmezzük például egy kohászati kemence

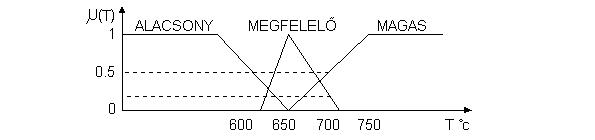
hőmérsékletére. Képezzük az alacsony, megfelelő, ill. magas nyelvi változók szerinti hőmér-

sékletek fuzzy halmazát (7.3. ábra).

7.3. ábra. Alacsony, megfelelő, magas fuzzy halmazok

Példánkban 750^oC-nál nagyobb hőmérséklet egyértelműen            magas, azaz a tagsági

függvény értéke 1. A 650^oC alatti hőmérsékletről egyáltalán nem magas, azaz a tagsági

függvény értéke 0. A két érték közötti hőmérsékleten a tagsági függvény értéke fokozatos,

lineáris átmenettel 0 és 1 közötti.

A fuzzy halmazok közötti fokozatos átmenet miatt a hőmérséklet egymást átfedő in-

tervallumokra osztható. Így lehetséges, hogy egy adott hőmérséklet egyszerre több halmazba

is tartozik különböző tagsági értékkel. Példaként a 700^oC a magas halmazba tartozik 0,5-ös

tagsági értékkel és a megfelelő halmazba 0,25-ös tagsági értékkel. Ebben az értelemben a

fuzzy halmazokat használjuk a nyelvi kifejezések megjelenítésére. Az egyes halmazokat

viszonylagosnak kell értelmezni, mivel egy másik hevítendő anyag szempontjából egész más

hőmérsékletértékek jelenthetik az alacsony, megfelelő, magas fuzzy halmazokat.

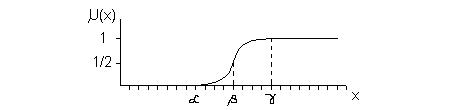
A fuzzy halmazok alakja az adott alkalmazástól függ. A 7.4. ábrán trapéz alakú (

funkció) fuzzy halmazt láthatunk.

7.4. ábra. Trapéz alakú fuzzy halmaz definiálása

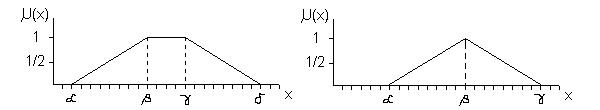
A  funkció tagsági függvénye négy paraméterrel van definiálva a (7-5) szerint:

X ≤ α

(X, α,β, γ δ

X− α     β − α

α ≤ X ≤ β

β ≤ X ≤ γ

, )

− γ δ − γ

1 X

γ ≤ X ≤ δ

X ≥ δ

A leggyakoribb háromszög alakú (∧) fuzzy halmazt szemlélteti a 7.5. ábra.

7.5. ábra. Háromszög alakú fuzzy halmaz definiálása

A ∧ funkció három paraméterrel definiálható a (7-6) szerint.

X α

≤

^X β α

X β

∧ X,α,β, γ

≤ ≤

X

X γ

X     γ

A fuzzy halmazokat nem csak egyenes vonalakkal definiálhatjuk. Leggyakrabban a

Gauss-féle harang-, ill. a Zadeh-féle S funkció használatos. Utóbbit a 7.6. ábra szemlélteti.

7.6. ábra. S alakú fuzzy halmaz

7.2.3. Műveletek fuzzy halmazokkal

Az első műveleteket a fuzzy halmazokkal Zadeh a             komplemens, a metszet és az unió hal-

mazműveletek alapján alkotta meg. A műveletek a Boole-algebrából ismert NEM, ÉS, ill.

VAGY műveletek kiterjesztésének is tekinthetők.

7.2.3.1. Fuzzy komplemens (NEM művelet)

A fuzzy komplemens az alábbiak szerint definiálható (7-8). Valamely A fuzzy halmaz

komplemensének nevezzük az X univerzumon azt az A halmazt, amelynek tagsági

függvényértékei:

. (7-7)

µ_A

1 − µ_A

∀x X

A felírásból kiderül, hogy a fuzzy logikában a NEM kapcsolatot a

komplemensképzéssel helyettesítjük.

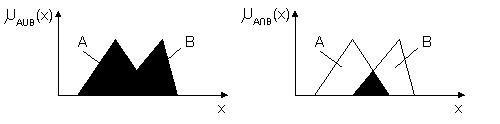
A fuzzy komplemensképzését szemlélteti a 7.7. ábra.

7.7. ábra. Fuzzy komplemens szemléltetése

7.2.3.2. Fuzzy halmazok uniója (VAGY művelet)

Az A és B fuzzy halmazok uniójának nevezzük azt az A ∪ B halmazt, amelynek tagsági

függvényértékei:

∈ .

µ_A∪B⁼max µ_A, µ_B

∀x X

A fuzzy halmazok unióját maxműveletnek, ill. általánosított változatát S normának

nevezik. A fuzzy unió művelet szemléltetése a 7.8. ábrán látható.

7.8. ábra. Fuzzy halmazok uniója (maxművelet, VAGY)

7.2.3.3. Fuzzy halmazok metszete (ÉS művelet)

Az A és B fuzzy halmazok metszetének nevezzük azt az A B∩           halmazt, amelynek tagsági

függvényértékei:

[ ( ) ] ∀x ∈ X                                 (7-9)

µ_A∩B⁼min µ_A, µ_B

A felírásból kiderül, hogy a fuzzy logikában az ÉS kapcsolatot minműveletnek, ill. ál-

talánosított változatát T normának nevezik. A fuzzy metszet fogalmát a 7.9. ábrán mutatjuk

be.

7.9. ábra. Fuzzy halmazok metszete (minművelet, ÉS)

7.2.3.4. Az unióra, a metszetre és a komplemensre vonatkozó szabályok

a)

A ∩ A ≠ 0 .

Ezt szemlélteti a 7.10a ábra.

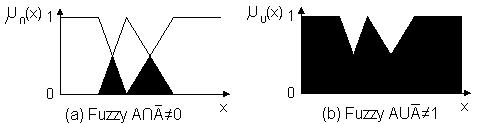
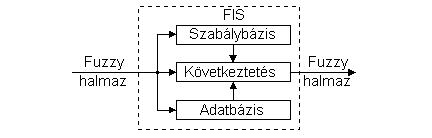
b)

A ∪ A ≠ 1 .

Ezt szemlélteti a 7.10b ábra.

7.10. ábra. Komplemens fuzzy halmazok metszete (a), és uniója (b)

7.3. Fuzzy következtető rendszer

A fuzzy halmazokat és a fuzzy halmazokon értelmezett műveleteket felhasználva létre lehet

hozni egy fuzzy következtető rendszert vezérlési és/vagy szabályozási célra. Ezen szabály-

rendszernek több elnevezése használatos:

Fuzzy Inference System (FIS), fuzzy következtető rendszer;

Fuzzy Rule Based System (FRBS), fuzzy szabálybázis;

Fuzzy Associative Memory (FAM), fuzzy asszociatív memória.

A fuzzy következtető rendszer három komponenst tartalmaz: szabálybázist (rule

base), adatbázist (data base), amelyek definiálják a tagsági funkciókat, valamint a következ-

tető mechanizmust (inference engine).

A fuzzy következtető rendszer felépítése a 7.11. ábra szerinti.

7.11. ábra. A fuzzy következtető rendszer (FIS) elemei

Az irányítástechnikai alkalmazásokban a jelek rendszerint konkrét (crisp) értékükkel

állnak rendelkezésre, ezért a jelekből előbb fuzzy halmazokat (tagsági függvényeket) kell

létrehozni, majd a következtetést fizikai jellé kell visszaalakítani. Irányítástechnikai célra a

Mamdani és a Sugeno-Takagi modell terjedt el.

A Mamdani típusú fuzzy irányító rendszert a 7.12. ábra szemlélteti.

7.12. ábra. Mamdani típusú fuzzy irányító rendszer

A fuzzifikáló egység (minősítőegység) a jel(ek) számszerű értékét minősíti, milyensé-

gi osztályba sorolja. Valamely osztályba tartozás mértékét a tagsági függvény alapján hatá-

rozhatjuk meg. A fuzzifikáló egység generálja a fuzzy halmazokat a bemenőjelből, vagyis

meghatározza a fuzzy változók tagsági fokait. A fuzzifikáló egység a fizikai változóból (jel-

ből) nyelvi változót generál. A fuzzifikálás átalakítási (transzformálási) művelet során a jel

számszerű (crisp) értékei leképződnek a jel milyenséget tartalmazó minősítési (fuzzy) hal-

mazba.

A fuzzy következtető rendszer a bemeneti fuzzy halmazból kimeneti fuzzy halmazt ge-

nerál. A szabályrendszer minden szabálya két részből áll: a bemenetének tekinthető feltétel-

rendszerből (conditions vagy más néven antecedent) és a következtetésből (consequent).

A szabályrendszer létrehozásához a következő feltételek szükségesek

a be- és kimeneti jelekhez olyan milyenségek tartoznak, amelyek igazságtartalmát

0 és 1 közötti értékkel jellemezzük (0, nem igaz, 1, igaz);

a feltételrendszerben az AND-, ill. OR-operátorok is használhatók. Ezek figye-

lembevételekor a fuzzy logika esetén a min-, ill. maxműveleteket alkalmazzuk;

a be- és kimenetek közötti összefüggéseken alapuló milyenségeket használó sza-

bályrendszer alapján rendszerint az IF....THEN (ha...akkor) típusú szabályok alkalmazásával

meghatározzuk a kimeneti jelek milyenségi halmazába való tartozást, valamint a feltétel-

rendszer számszerű kiértékelésével a halmazhoz való tartozás fokát.

A kimeneti fuzzy halmazt a szabályozóban fizikai jellé kell alakítani a defuzzifikáló

egységgel. A defuzzifikáció során a szabálysorok által meghatározott összevont fuzzy hal-

mazhoz számértéket rendelünk, ami a fuzzy következtető rendszer kimenőjele lesz. A lekép-

zés nem egyenértékű művelet, ezért a létrehozandó kimenőjel előállítására több módszer

terjedt el (lásd a 7.4. alfejezet).

A következtető rendszert rendszerint HA A (feltétel) ÉS B (feltétel) .... AKKOR Y

(következmény) alakban célszerű felírni. A Mamdani féle HA...AKKOR következtető rend-

szert szemlélteti a 7.13. ábra.

Például: HA a hőmérséklet      magas és a nyomás nagy, AKKOR a beavatkozójel le-

gyen alacsony.

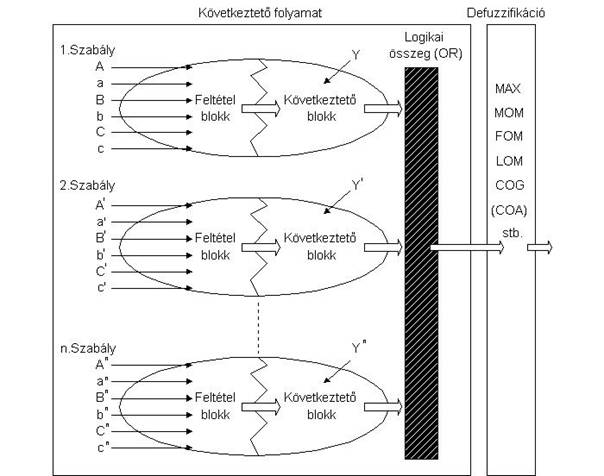
7.13. ábra. Mamdani típusú FIS szemléltetése

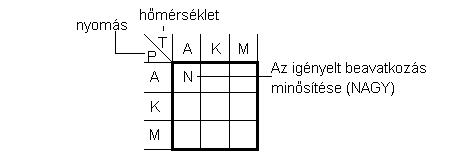
Az összefüggéseket valamennyi, a példában előforduló változatra fel kell írni egy

táblázatba foglalva, amelynek egyik (pl. vízszintes) oldalán az egyik bemeneti változó minő-

sített értékeinek variációit (pl. alacsony, közepes, magas), másik (pl. függőleges) oldalán a

másik bemeneti változó minősített értékvariációit írjuk. A táblázat egyes rubrikáiba a kime-

neti változó minősített értékei kerülnek a 7.14. ábra szerint.

7.14. ábra. Fuzzy szabályrendszer táblázatba foglalása

A fuzzy következtető rendszer szabálybázisának annyi HA...AKKOR következtetés-

ből kell állnia, hogy a bemeneti minősített nyelvi változók valamennyi előforduló kombiná-

ciójához egyértelmű kimeneti következményt rendeljünk (a példában 3 x 3 = 9). A 7.14. áb-

rán bejelölt cella az alábbi szabályt fejezi ki:

HA a hőmérséklet (T) alacsony ÉS a nyomás (P) alacsony, AKKOR a beavatkozás nagy.

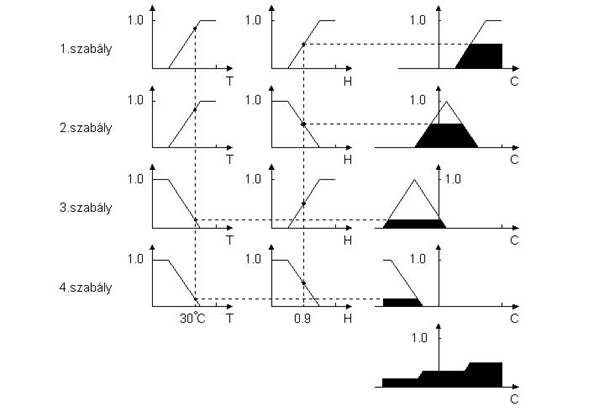
A fuzzy következtető rendszer szemléltetésére a 7.15. ábrán egy légkondicionáló

négy szabályának minművelettel előállított részhalmazát és a maxművelettel képzett logikai

összegét mutatjuk be. A bemeneti változók: hőmérséklet (T), páratartalom (H), kimenőjel:

irányított jellemző (C). Az ábrán        T = 30 ^oC és H = 0,9 értékek esetén képződő értékek van-

nak jelölve. A példában a kimenőjel kétféle polaritású lehet. A minművelet esetén a kisebbik

érték határozza meg a hozzá tartozó kimeneti halmazt. A kimenőjel a részhalmazok

maxműveleteként adódik. Ez az érték kerül a defuzzifikáló egység bemenetére.

7.15. ábra. Kimenő fuzzy halmaz létrehozása

7.4. Defuzzifikációs módszerek

A defuzzifikáció során a szabálysorok által meghatározott összevont fuzzy halmazhoz szám-

értéket (crisp) rendelünk, ami a fuzzy szabályozó kimenőjele lesz. Az érték meghatározására

több módszert dolgoztak ki, közülük a leggyakoribbakat mutatjuk be. A módszerek kiválasz-

tása lényeges, mert az egyes módszerek eredménye hat a szabályozó tulajdonságaira.

7.4.1. Maximumkiválasztó eljárás (max.)

Ez az eljárás a legmagasabb tagsági fokkal teljesülő termet választja ki és azt az értéket

(Xm) jelöli meg eredménynek, ahol az adott term a maximumát éri el (7.16. ábra). Szimmet-

rikus függvény esetén ez a szimmetria tengely helye.

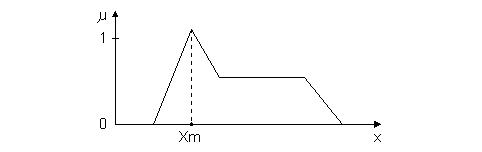
7.16. ábra. Maximumkereső defuzzifikáció

A maximális tagsági függvény a következő összefüggéssel állapítható meg:

( ) xm ∈ x.

µ x    m⁼max µx

A 7.15. ábrán a kimenőjel defuzzifikált értéke xm.

Ez a módszer csak csúcsos függvény esetén ad egyértelmű megoldást, amikor egy

maximum van. A módszer nagy előnye a rendkívül kis számítási igény és az ebből következő

igen rövid számítási idő, ami szabályozó esetén gyors működést jelent.

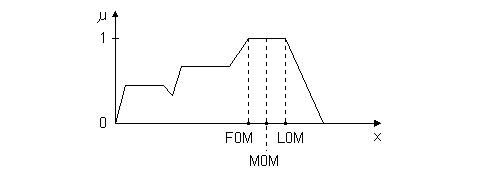
Olyan fuzzy halmazok esetén, amelyeknél több maximumhely van, vagy a maximális

tagsági fok vízszintes, a MAX módszer kiküszöbölésére a FOM, MOM, ill. LOM eljárást

használják. A FOM (First of Maximum) első maximum, a LOM (Last of Maximum) utolsó

maximum és a MOM (Mean of Maximum) maximum-átlagérték típusú defuzzifikációt a

7.17. ábra szemlélteti.

7.17. ábra. FOM, MOM, LOM típusú defuzzifikáció

7.4.2. Súlypontszámító eljárás (Centre of Gravity, COG)

A súlypontszámító eljárás az összevont fuzzy halmaz súlypontjának helyét jelöli ki, és tekinti

eredménynek. Az eredmény a következő összefüggéssel számítható:

l

∑ µ( )

Xmj Xmj

X

j

l

Xmj

j  1

ahol µ Xmj a j-edik term tagsági foka a maximumhelyen (Xm). A COG defuzzifikációs

módszert a 7.18. ábra szemlélteti.

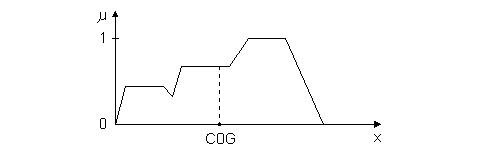
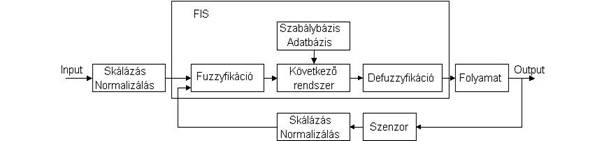
7.18. ábra. Súlypontkereső (COG) eljárás

Az egyes defuzzifikálási módok meghatározzák a szabályozó működését. A MAX és

a MOM eljáráskor a rendszer viselkedése hasonlít a többállású szabályozó működésére, míg

a COG eljárás esetén a PI szabályozóra. Ezért a COG pontosabb beállást eredményez, míg a

másik kettő kisebb tranziensjelenséget. A MOM stratégia mindig jobb eredményt ad a MAX

eljárásnál. A MAX eljárás igényli a legkisebb számítási kapacitást, tehát a leggyorsabb, míg

a COG a legnagyobbat, ezért a leglassúbb.

7.5. Fuzzy szabályozó tervezése

A fuzzy szabályozó tervezésének lépései:

a fuzzy szabályozó modell megválasztása;

a fuzzy szabályrendszer kidolgozása;

a fuzzy szabályozó behangolása.

A fuzzy szabályozásokhoz többféle modell került kidolgozásra, pl. a már említett

Mamdani-modellen kívül a Sugeno-Takagi-modell.

A fuzzy szabályrendszer kidolgozása az előzőekben leírtak szerinti. Az ismert PD-,

PI-, ill. PID-szabályozók a fuzzy szabályrendszer megfelelő kialakításával közelíthetők. Pél-

daként a PD-szabályozót úgy foghatjuk fel, mint egy relációt a hibajel (e), a hibajel megvál-

tozása (∆e) és a kimenőjel (c) között:

HA a hibajel (e) kicsi és a ∆e közepes, AKKOR a c kicsi,

HA e közepes és ∆e nagy, AKKOR c közepes stb.

A PD jellegű fuzzy szabályozó szabálybázisának általános alakja:

HA e = feltétel ÉS ∆e = feltétel, AKKOR c = következtetés.

A Mamdani-féle fuzzy következtető rendszerrel a 7.19. ábra szerint épül fel a fuzzy

szabályozókör.

7.19. ábra. Mamdani-féle fuzzy szabályozókör

A szabályok forrása és származtatása:

a szakértői ismeretek és a mérnöki tapasztalat alapján (pl. szakmai leírások, üze-

meltetési könyvek, kérdőív);

a kezelőszemélyzet beavatkozásainak megfigyelése alapján;

a folyamat fuzzy modelljének (leírásának) felállítása alapján, tanulórendszerek

felépítésével.

A fuzzy szabályozó behangolását a következők figyelembevételével végezhetjük. A

fuzzy szabályozók esetén különös jelentősége van a szabályozó behangolásának, mivel a

szabálybázis igen nagyfokú közelítést és szabadságot jelent. Egyrészt az egyes nyelvi válto-

zókat konkrét tagsági értékkel kell helyettesíteni a konkrét futtatható algoritmus kidolgozá-

sához, másrészt a szabálybázis megalkotásakor nem vagy csak részben vagyunk tekintettel a

szakasz dinamikai tulajdonságaira. Belátható, hogy pl. egy fuzzy jellegű helyzetszabályo-

zásnál nem közömbösek a hajtómű és a szakasz dinamikai tulajdonságai. Tehát a fuzzy sza-

bályozó tervezésénél nem a szabálybázis megalkotása a nehéz feladatot, hanem az optimális

működésű szabályozó behangolása.

A fuzzy szabályozó behangolását segítő tényezők:

kellő gyakorlat hasonló funkciójú fuzzy szabályozó behangolása alapján;

kísérleti úton, nagyszámú mérési sorozat felhasználásával (kísérleti hangolás);

optimumkereső genetikus algoritmus felhasználásával.

Részben a fentiekkel indokolható, hogy fuzzy szabályozókat főként a szakasszal egy-

beépítik és gyárilag behangolják (pl. ABS fékrendszer, kamerafókuszálás, mosógép-, ill.

légkondicionáló-irányítás stb.). Külön nehézséget jelent a fuzzy szabályozók tervezésénél a

rendszer stabilitásának biztosítása.

7.6. Fuzzy szabályozók stabilitása

A klasszikus szabályozáselmélet több módszert dolgozott ki a szabályozott rendszerek stabi-

litásának vizsgálatára (Routh-Hurwitz, Nyquist, Bode stb), amelyek feltételezik a szabályo-

zott szakasz és a szabályozó egzakt matematikai modelljét. Ha mindkét modell lineáris, foly-

tonos és időfüggetlen, akkor ezen módszerek jól alkalmazhatók. A fuzzy szabályozók nemli-

neárisak és általában ott alkalmazzák, ahol az előbbi követelmények nem teljesülnek. A

fuzzy szabályozások is visszacsatolt rendszerek, így a stabilitási kérdések fontosak. Az alap-

vető probléma, hogy a fuzzy modell kvalitatív modell, amely szubjektív becslésen alapul. A

visszacsatolt rendszer stabilitása viszont csak kvantitatív információ alapján határozható

meg egzaktul.

A jelenleg kidolgozott stabilitásvizsgálati módszerek alkalmazhatósága szempontjá-

ból a fuzzy szabályozókat négy osztályba sorolják:

1. osztály: a folyamatmodell ismert és lineáris, a fuzzy szabályozó közvetlen sza-

bályozást végez;

2. osztály: a folyamatmodell ismert és nem lineáris, a fuzzy szabályozó közvetlen

szabályozást végez;

3. osztály:

a folyamatmodell ismert (lineáris vagy nem lineáris), a fuzzy szabá-

lyozó felügyeleti vagy adaptív fuzzy szabályozó;

4. osztály: a folyamatmodell fuzzy jellegű, a fuzzy szabályozó közvetlen szabá-

lyozást végez.

Az első három osztályra vannak részben kidolgozott stabilitásvizsgálati módszerek

(mivel mindhárom a folyamatmodell mennyiségi, matematikai ismertségét feltételezi), de

ezek sem általános módszerek, hanem a klasszikus módszerek adaptálásai. Amennyiben nem

a kvantitatív, hanem a kvalitatív modell ismert, arra az esetre nincs kidolgozott, már a terve-

zés során alkalmazható stabilitásvizsgálati módszer.

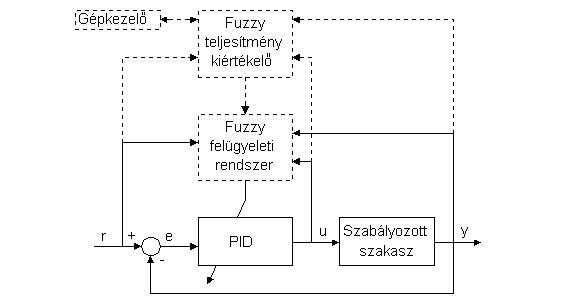
7.7. Fuzzy felügyeleti rendszer PID-szabályozóhoz

Az iparban sok technológiai folyamatot PID-szabályozóval irányítanak [13]. Előnyei ellené-

re, a hagyományos szabályozó hátránya, hogy át kell hangolni, ha változnak a működési

feltételek. Ezt a hátrányt lehet csökkenteni a fuzzy felügyeleti rendszer alkalmazásával,

amely az alacsony szintű szabályozó paramétereit hangolja (7.20. ábra).

7.20. ábra. Fuzzy felügyeleti szabályozó

A szakemberektől (gépkezelőtől) általában megszerezhető egy szabályhalmaz, amely

pl. a P és a D tag erősítési értékeire (Kp és Kd) vonatkozik az aktuális (r) beállított érték ese-

tén. A szabályok például a következő formában jelenhetnek meg:

HA r alacsony, AKKOR Kp legyen magas és Kd alacsony,

HA r magas, AKKOR Kp legyen alacsony és Kd közepes.

A következtető rendszer ugyanúgy működik, mint a közvetlen irányításé. A szabá-

lyok egy szakember hangolási stratégiájának nyelvi leírását tartalmazzák. Az alacsony szin-

tű szabályozó lehet pl. hagyományos PID-szabályozó vagy PID-szerű fuzzy szabályozó.

A fuzzy felügyeleti rendszer kiegészíthető fuzzy teljesítménykiértékelővel is. A fo-

lyamat változásainak megfelelő paraméterbeállítás helyett ez a struktúra a rendszer válaszát

elemzi, és ez alapján hangolja az alacsony szintű szabályozót. A rendszer válaszát a túllövés,

beállítási idő és más minőségi jellemzők szerint minősíti. A következő példa egy lehetséges

teljesítménykiértékelő szabály lehet.

HA a túllendülés kicsi ÉS a felfutási idő közepes ÉS a kritérium értéke kicsi, AKKOR

a teljesítmény jó.

7.8. Fuzzy funkciók megvalósítása PLC-vel

A fuzzy szabályozó algoritmusok analóg és digitális jelfeldolgozással egyaránt megvalósít-

hatók. Néhány tipikus megoldás: általános szóprocesszorral vagy mikrovezérlővel, speciális

analóg vagy digitális fuzzy processzorral és PLC-n belüli célhardverrel és szoftverrel.

A valós idejű változat egyik tipikus megoldása a hagyományos PLC hardverének és

szoftverének bővítése fuzzy funkciót ellátó modullal: pl. a Siemens, Klöckner-Moeller,

Omron PLC-k ilyenek.

A szoftver kifejlesztéséhez rendszerint grafikus fejlesztőrendszer áll rendelkezésre. A

program beépített szimulátorral validálható. A validált programot a számítógép a                  real-time

hardverelem (PLC, µP, mikrovezérlő) interpretere számára érthető formátumra vagy gépi

kódjára fordítja és letölti. Egy Siemens PLC-be épített fuzzy modul katalógusbeli jellemzőit

a következőkben adjuk meg:

bemenetek száma: max. 8, egyenként 7 tagsági függvénnyel;

kimenetek száma: max. 4, egyenként 9 tagsági függvénnyel;

szabályok száma: max. 200;

válaszidő: min. 0,54, max. 1,91 ms.

A Siemens gyártmányú fuzzy szabályozó tervezését a FUZZY WINCC grafikus

szoftver segíti.

Az Omron CS1 PLC fuzzy modelljének adatai:

a fuzzy modul típusa: FZ-001;

bemenetek (feltételek) száma: 8;

kimenetek (következtetések) száma: 2;

szabályok száma: max. 128;

válaszidő: ~ 6 ms.

7.9. Tervezési példa: a fordított működésű inga egyensúlyozása

A következőkben az irodalomból jól ismert fordított működésű inga (inverted pendulum)

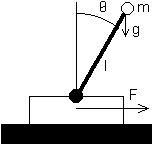
szabálybázisának tervezését mutatjuk be. A fordított működésű inga a 7.21. ábrán látható.

7.21. ábra. A fordított működésű inga

Az irányításhoz a dőlésszög mérésére és a dőlésszögváltozás sebességének

d Θ meghatározására van szükség. A dőlésszöget rendszerint inkrementális jeladóval mérik,

a szögsebességet ennek differenciálásával állítják elő. A szabályozás célja a fordított műkö-

désű inga függőleges helyzetben tartása, amely az inga talppontjának mozgatásával érhető el

a ± F erőt biztosító szervomechanizmus közbeiktatásával egy ± dV vezérlőjellel. A szabá-

lyozónak Θ , d Θ két emenőjele és egy dV kimenőjele van. A probléma hasonlít egy pálca

függőleges kézi egyensúlyozásához.

A bemeneti változókat három értékre osztva: kicsi, small (S), közepes, medium (M),

és nagy, large (L), valamint a két irányt figyelembe véve, negatív (N), pozitív (P), az alábbi

tagsági függvényeket kapjuk:

NL, negatív nagy

NM, negatív közepes

NS, negatív kicsi

ZR, zérus (megfelelő)

PS, pozitív kicsi

PM, pozitív közepes

PL, pozitív nagy.

A szabályozási feladatot hét szabállyal írhatjuk le az előforduló változatoknak megfe-

lelően a 7.1. táblázat szerint.

7.1. táblázat. Szabálybázis a fordított működésű inga egyensúlyozásához

Szabályok

Feltételek

Következmény

1. szabály

Ha az inga mérsékelten dől balra ( =PM), és a   akkor az inga talppontját közepes sebességgel balra kell

dőlésszögváltozás sebessége közel zérus (d mozgatni (dV = PM)

ZR)                                      akkor dV = PM

Ha = PM és d = ZR

2. szabály

3. szabály

4. szabály

5. szabály

6. szabály

7. szabály

Ha = PS és d = PS

Ha = PS és d = NS

Ha = NM és d = ZR

Ha = NS és d = NS

Ha = NS és d = PS

Ha = ZR és d = ZR

akkor dV = PS

akkor dV = ZR

akkor dV = NM

akkor dV = NS

akkor dV = ZR

akkor dV = ZR

A 7.1. táblázat szerinti szabályokat a 7.22. ábra szemlélteti.

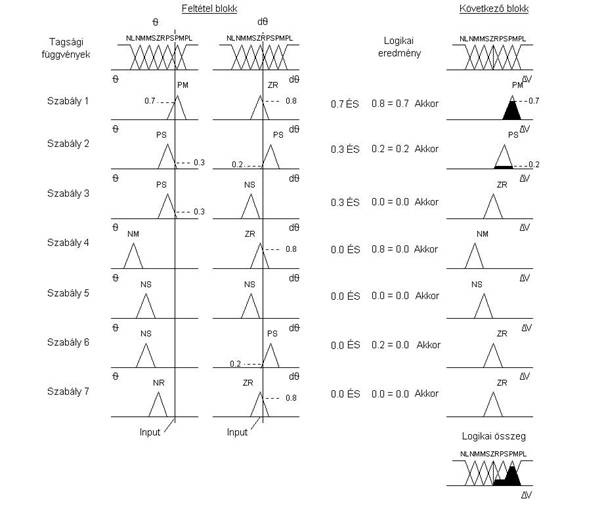
7.22. ábra. A szabálybázis a 7.1. táblázat alapján

Az ábrán a teljes fuzzy következtető rendszert és a visszaalakítás folyamatát is nyo-

mon követhetjük, egy konkrét Θ és d Θ érték esetén a (∆V) kimeneti érték képzése is látha-

tó. Az 1. szabály esetén a közepes dőlésszög (tagsági értéke 0,7), a d Θ tagsági értéke 0,8. A

fuzzy min- (ÉS) művelet eredménye 0,7. Hasonlóképpen a második szabályon belül a kis

dőlésszög (PS = 0,3), a d Θ pozitív kis értékű (PS = 0,2), a fuzzy minművelet eredménye 0,2.

A vizsgált esetben a többi szabály 0 értékű, így az első két szabály logikai összege (fuzzy

maxművelet eredménye) kerül a visszaalakító (defuzzifikáló) egység bemenetére. A vissza-

alakítás többféle algoritmus szerint végezhető el. A példa az OMRON ELECTRONICS

nyomán az AMIRA laboratóriumi modellen, ill. fejlesztőrendszeren készült. A fenti szabá-

lyokat a feladat minőségi modellje alapján határozták meg a modell mennyiségi jellemzőit

(ingahossz, tömeg stb.) nem vették figyelembe.

Irodalomjegyzék

I. Ajtonyi: Intelligent Control System. Habilitation Dissertation.

Kosice, 1998.

Horváth G.: Neurális hálózatok és műszaki alkalmazásaik.

Budapest, BME - 10018, 1995.

Vörös G.: Bevezetés a neurális számítástechnikába.

Budapest, LSI Oktatóközpont, 1997.

Kónya L.: Minősítő szabályozás I-IV.

MARKInfo, 1995.

Kóczy T. L., Tikk D.: Fuzzy rendszerek.

Budapest, Typotex Kiadó, 2000.

I. Ajtonyi: System Modelling. Proc.: TEMPUS S JEP MODIFY 07759/94

Miskolc, 1997.

C. T. Lin, C. S. G. Lee: A Neuro-fuzzy Synergism to Intelligent Systems.

Prentice Hall PTR, Upper Saddle River, 1996.

Ajtonyi I.: Digitális rendszerek.

Miskolc, Egyetemi Kiadó, 1998.

SIEMENS: PCS7 gépkönyv, 1997.

[10] OMRON: CS1 Users Manual, 1999.

[11] T. J. Ross: Fuzzy Logic with Engineering Application.

McGraw Hill Company, 1998.

[12] L. Madarász: Metodika Situačného Riadenia A Jej Aplikácie, 1995.

[13] Szemes G.: Bevezetés a fuzzy logika irányítástechnikai alkalmazásába.

Paks, Főiskolai jegyzet, 1996.