Pénzügyi számítások

Matematikai alapok:

Mértani sorozat:

Az első n elem összege:

hatványozás azonosságai alapján:

aⁿ - bⁿ = (a-b)(a^n-1+a^n-2b+a ^n-3b²+.ab^n-2+b^n-1)

qⁿ - 1ⁿ = (q-1)(q^n-1+q^n-2+q^n-3+..q+1)

Kamatszámítás

Kamatláb: 100 pénzegység meghatározott időre -kamatidő- vonatkozó kamata. P %-ban adjuk meg.

A kamatidő alapesetben egy év.

A kamatperiódus az az időt 424e49e artam. amilyen gyakorisággal a kamatokat meghatározzák.

lehet: 1 nap, 1 hónap, x hónap, egy év, több év.

T₀- a 0 időpontbani pénzösszeg

P- kamatláb %

p =

K- a kamat összege

1 évre szóló kamat kiszámítása:

Egy évnél rövidebb, de éven belüli kamat kiszámítása:

365 napos évvel számítva

n a kérdéses időszak napjainak száma

        tőkenövekmény

(előfordul, hogy a bank 360 napos évvel és 30-napos hónappal számol- (ez egyszerűsítés)

Követelésünk:  Alapösszeg+kamat

Példa:

Befizetünk év elején 25 000 Ft, a kamatláb 14%. Mennyi a követelésünk

a)          143 nap múlva

b)         1 év múlva

c)          1 év 143 nap múlva

d)         10 év múlva

a)          T₀+T₀(p)= T₀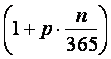 25 000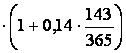= 26 371 Ft.

b)         T₀+T₀p=T₀(1+p)
25 000(1,14)= 28 500 Ft.
az (1+p) =q                       kamattényezőnek hívjuk

c)          A második év elején a kamattal megnövelt összegről indulunk, és az kamatozik még 143 napig:
T₀(1+p)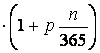

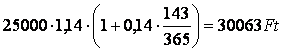
d)         első év végén:                                T₀q
második év végén: (T₀q)q=T₀q²
harmadik év végén: q=T₀q³

n-dik év végén T₀qⁿ
tizedik év végén: T₀q¹⁰=25 000*1,14¹⁰=92680 Ft.

Diszkontálás

Amikor ismerjük a kamatokkal megnövelt értéket, és visszafelé számítjuk ki a múltbeli alapösszeget.

Vagy: Ismerjük a jövőbeni értéket és a jelenértékre vagyunk kiváncsiak.

Pl.  Jelenleg van 100 000 Ft-om a bankban. Mennyi volt az alapösszegem három évvel ezelőtt, ha a bank évi 6% kamatot fizetett és ez nem változott az évek során.

T₀q³=100000                                q=1,06

T₀== Ft                ez az un. diszkontált érték

a    diszkonttényező

A diszkonttényező az egy év múlva esedékes egységnyi pénz jelenbeli értékét kifejező szorzószám.

Az infláció figyelembe vétele

Pl.

10 000 Ft-t 10 évre 12%-os kamatra kölcsönadunk.

Az infláció mértéke évi 7% (tegyük fel, hogy nem változik az évek során)

Kérdés: a 10. év végén mekkora a rendelkezésünkre álló pénz vásárlóértéke?

A tőke felnövekedett értéke:

10 000 * 1,12¹⁰=10 000*3,1058=31058 Ft.

A jelenlegi 10 000 Ft vásárlóértéke 10 év múlva:

10 000*1,07¹⁰=10 000*1,9672=19 672 Ft.

A tényleges nyereségünk 10 év múlva a két összeg különbsége:

(31 058 -19 672) = 11 386 FT

Ennek a jelen értéke:

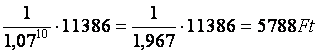
Viszonyítva ezt a 10 000 Ft befektetéshez- a befektetés reális nyeresége 57,9%.

A kamatperiódus végén a kamatokat vagy kifizetik(a),  vagy hozzáírják a tőkéhez(b).

a)      egyszerű kamatozás

b)      kamatos kamatozás

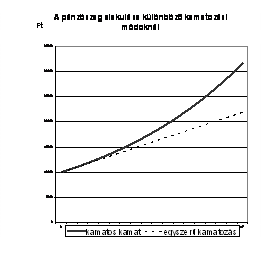
Egyszerű kamatozásnál a felszaporodott tőke:

Kamatos kamat esetén a a felszaporodott tőke:

Járadékszámítás

Az egyenlő időközökben fizetett összegek sorozatát járadéknak nevezzük.

Cél:                 a) tartozás kiegyenlítése-törlesztőjáradék

b)pénzösszeg gyűjtése- gyűjtőjáradék

Egyszerűsítő feltélek:

A befizetési időközök megegyeznek a kamatidővel

Minden alkalommal ugyanakkora összeget fizetünk be

Gyűjtőjáradék

Évi P% kamatláb mellett minden év elejen befizetünk a összeget. Kérdés, hogy az utilsó befizetés után egy évvel mekkora összeg áll rendekezésünkre? 

Jelöljük ezt: S_n⁽¹⁾-gyel   Az ⁽¹⁾ azt jelöli, hogy egy évvel az utolsó befizetés után..

S_n⁽¹⁾=a(1+p)ⁿ=aqⁿ

Ha az utolsó befizetés után nem várunk egy évet:

S_n=a

Pl:

5 év múlva meg akarunk vásárolni egy 4 000 000 Ft értékű autót. Mennyi pénzt kell évente (január 1-én) elhelyezni a bankban 15%-os kamatláb mellett hogy rendelkezésre álljon a szükséges pénz?

S₅⁽¹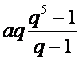⁾= ahol q=1,15

4 000 000=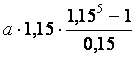=7,753738a

a=515 880 Ft

Kölcsöntörlesztés

T₀ összegű kölcsönt veszünk fel P%-os kamatra, évente a összeget fizetünk vissza. Az n-dik év után mennyi lesz a tartozásunk?

p=                                   q=1+p

1. év után:        T₀q-a

2. év után:        (T₀q-a)q-a= T₀q²-qa-a

3. év után:                    (T₀q²-qa-a)q-a=T₀q³-q²a-qa-a=
T₀q³ -a(q²+q+1)

(q²+q+1)(q-1)=q³-1 összefüggés alapján

ill.

(q^n-1+q^n-2+..q+1)(q-1)=qⁿ-1

n. év után:        T₀qⁿ-a

A kölcsönünk lejár, ha T₀qⁿ-a=0

Pl.

400 000 Ft-t veszünk fel 12%-os kamatra, évi 50 000Ft-t törlesztünk

8 év után a tartozásunk:

Mennyi a törlesztő részlet, ha 10 év alatt vissza akarjuk fizetni a kölcsönt?

T₁₀=0

Vagyis, ha évente 70 794 Ft-t fizetünk vissza, akkor 10 év alatt lejár a kölcsönünk.

Havi törlesztés

S összeget veszünk fel P% kamatra, havonta a összeget törlesztünk, n évig

p=;           q=1+p

A törlesztést az első hónap végén kezdjük.

Az első év végén az adósságállomány:

m=12 periódusra osztva az évet:

S₁= Sq-                    (*)

Összevonva:

S₁=Sq-

Általánosan:

S₁= Sq- Sq-

Az n. év után:

S_n= Sqⁿ-  Ez az un. utólagos befizetés esetén.

Ha un. előzetes befizetésről van szó (pl. gyűjtünk valamire), akkor a *-gal jelölt egyenletben a zárójelen belül nem 11, hanem 12 tag van, így az első év végén a követelésünk:

K₁=

Általánosan:

K₁=

Az n. év után felvehető összeg:

K_n=