|  | ||||||||
|  | ||||||||
| | ||||||||
| | ||||||||
 |
kategória |  |
||||||||
|
|
||||||||||
 |
 |
|
|
|
|
|
||
|
|
Klimatológiai statisztika
A kiadott gyakorló
feladatok megoldása
1. Feladat
Tihanyban 22 év során 37 napon fordult elő 30 mm-t meghaladó 24 órai csapadék. Milyen valószínűséggel várható olyan év, amikor nem fordul elő 30 mm-t meghaladó csapadékmennyiség.
Alapkérdés:
Adott p valószínűségi alternatív esemény n esetből k-szori bekövetkezése milyen valószínűséggel várható.
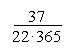Feladat típusMivel az alapkérdést alkalmazhatjuk és p = = 0,00467721 è p< 0,03
Ezért Poisson eloszlást alkalmazzuk.
Meghatározzuk a Poisson eloszlás paramétereit:
Paraméterek
n ˇ p ; k
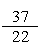
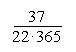
n ˇ p = 365 ˇ = = 1,681818
k = 0
Felírjuk a Poisson eloszlás képletét:
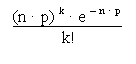
P(k ; n ˇ p) = e = 2,72
Behelyettesítünk a képletbe:
k = 0 ; n ˇ p = 1,681818
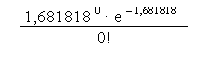
P(0 ; 1,681818) =
P(0 ; 1,681818) = 0,1860
Válaszolunk a feladatra:
Tehát annak a valószínűsége, hogy a kiindulási paraméterek szerint Tihanyban egy adott év során nem fordul elő 30 mm-t meghaladó csapadékmennyiség 18,6% a valószínűsége.
2. Feladat
Egy hegycsúcsra telepítendő TV-torony műszaki tervezéséhez szükséges annak ismerete, hogy egy adott évben 3 villámcsapás éri a csúcsot. A környéken végzett megfigyelések szerint 8 év során 19 db - hegycsúcsot ért - villámcsapást jegyeztek fel. Mekkora annak a valószínűsége, hogy egy évben 3 villámcsapás érje a csúcsot?
Alapkérdés:
Adott p valószínűségi alternatív esemény n esetből k-szori bekövetkezése milyen valószínűséggel várható.
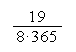Feladat típusMivel az alapkérdést alkalmazhatjuk és p = = 0,006506849 è p< 0,03
Ezért Poisson eloszlást alkalmazzuk.
Meghatározzuk a Poisson eloszlás paramétereit:
Paraméterek
n ˇ p ; k
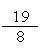
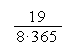
n ˇ p = 365 ˇ = = 2,375
k = 3
Felírjuk a Poisson eloszlás képletét:
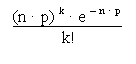
P(k ; n ˇ p) = e = 2,72
Behelyettesítünk a képletbe:
k = 3 ; n ˇ p = 2,375
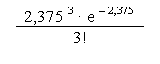
P(3 ; 2,375) =
P(3 ; 2,375) = 0,207677858
Válaszolunk a feladatra:
Tehát annak a valószínűsége, hogy egy évben 3 villámcsapás érje a hegycsúcsot 20,767%.
3. Feladat
Mi annak a valószínűsége, hogy egy adott helyen az év 12 hónapjából egynek sem lesz magasabb a középhőmérséklete a felső kvartilisnél?
Alapkérdés:
75%
Adott p valószínűségi alternatív esemény n
esetből k-szori bekövetkezése milyen valószínűséggel várható.
 |
Feladat típusBinomiális, mert p = 0,75
Meghatározzuk a Binomiális eloszlás paramétereit:
Paraméterek
p = 0,75
n = 12
k = 12
Felírjuk a Binomiális eloszlás képletét:
pk ˇ (1 - p) n-k
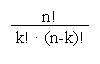
P(k ; n ) = ˇ
Behelyettesítünk a képletbe:
0,7512 ˇ (1 - 0,75) 12 - 12
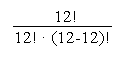
P(12 ; 12) = ˇ
P(12 ; 12) = 0,03167
Válaszolunk a feladatra:
Tehát annak a valószínűsége, hogy egy adott helyen az év 12 hónapjából egyiknek sem lesz magasabb a középhőmérséklete 3,167%.
4. Feladat
Winnipegben a januári középhőmérséklet -17,7°C a szórása pedig 4,1°C.
Normális eloszlást feltételezve határozzuk meg annak a középre szimmetrikus intervallumnak a végpontjait, amelyek közé az összes érték 50%-a esik!
Mivel hőmérsékletről van szó, ezért Normál eloszlást alkalmazunk.
Meghatározzuk a Normális eloszlás paramétereit:
Paraméterek
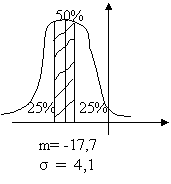m = -17,7
σ = 4,1
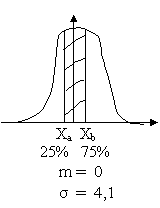
Oldjuk meg grafikusan a feladatot:
Annak a valószínűsége, hogy bármely X érték
kisebb legyen Xa - nál 25%
kisebb legyen Xb -nél 75%
P( X < Xa ) = F( Xa ) = 25%
P( X < Xb ) = F (Xb) = 75%
Annak a valószínűsége, hogy
P(Xa < X < Xb) = P(X < Xb) - P(X < Xa) = F(Xb) - F(Xa) = 75% -25% = 50%
Oldjuk meg számszerűen:
Xa - m σ Xa
X è == da è = da
F( da ) = 25% è da = -0,678
Xa = 4,1* ( - 0,678 ) + (-17,7 )
Xa = - 20,4798
F(d b ) = 75% è d b = 0,678
Xb = 4,1 ˇ 0,678 + (-17,7)
Xb = -14,9202
Xb = ( m - Xa) + m
Xb = (-17,7 - (-20,4798) ) + (-17,7 )
Xb = -14,9202
Válaszolunk a feladatra:
Tehát a kiindulási paraméterek szerint [ 14,9202 ;20,4798 ] intervallum az, amelybe a közepek 50%-os valószínűséggel esnek.
5. Feladat
Egy időszakos növényfaj létfeltételeihez szükséges, hogy a vegetációs időszakban uralkodó havi középhőmérsékletek legalább 40%-a 12°C fölött legyen. Az A és B észlelőhelyeken a vegetációs időszak havi közepeinek megfelelő paraméterei a következők:
A: m=11,5°C σ = 1 °C
B: m=11,0°C σ = 4 °C
Mivel hőmérsékletről van szó, ezért Normál eloszlást alkalmazunk.
Meghatározzuk a Normális eloszlás paramétereit:
Paraméterek
ma = -17,7 mb = 11,0
σa = 4,1 σb = 4
Oldjuk meg grafikusan a feladatot:
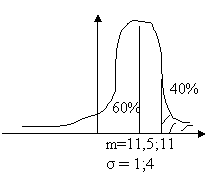Annak a valószínűsége, hogy a havi középhőmérsékletek legalább 40%-a
12°C fölött csak F( Xa) , F(
Xb ) = 60%-nál Xa , Xb ≥ 12°C esetén
lehet.
Oldjuk meg számszerűen:
Xa - m σ Xa
X è == da è = da
F( da ) = 60% è da = - 0,254
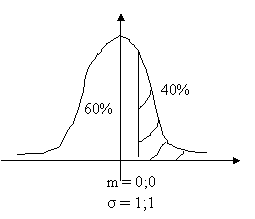Xa = 1* (- 0,254 ) + 11,5
Xa = 11,754
F( db ) = 60% è db = - 0,254
= 4 ˇ (- 0,254 ) + 11,0 111d34b
Xa = 12,017
Válaszolunk a feladatra:
Tehát a kiindulási paraméterek szerint az A észlelőhelyen nem lehetséges az adott növényfaj léte, de a B észlelőhelyen lehetséges!
6. Feladat
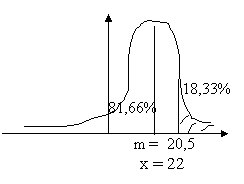
Szegeden az 1901-1960 közötti 60 év adatai alapján a júniusi középhőmérsékletek 20,5°C. Kizárólag a hőmérsékletek feltételezetten normális eloszlását felhasználva határozzuk meg a júniusi középhőmérsékletek szórását, ha tudjuk, a vizsgált 60 június közül 11-nek volt a középhőmérséklete legalább 22°C.
Mivel hőmérsékletről van szó, ezért Normál eloszlást alkalmazunk.
Meghatározzuk a Normális eloszlás paramétereit:
Paraméterek:
m = 20,5
x = 22
F(d) = 1-11/60 = 100% - 18,33% = 81,66%
Oldjuk meg grafikusan a feladatot:
F(d) = 81,66% ezért d = 0,907
X >= 22-nál, aminek 18,33% esélye van
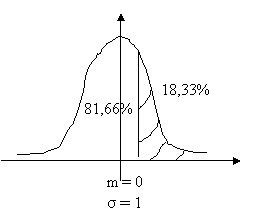Így az X =< 22-nek 81,66% esélye van
Oldjuk meg számszerűen:
X - m σ X - m d
= d è σ = = da
= = 1,654
Válaszolunk a feladatra:
Tehát a kiindulási paraméterek szerint a szórás 1,654°C
. Feladat
Tekintsünk egy adott helyre vonatkozó több éves hőmérsékleti sort. Ez a hőmérsékleti sor havi közepekből áll. Annak a valószínűsége, hogy egy tetszőleges hónap középhőmérséklete a több éves sor közepe fölötti 0,5 . Kiválasztva egy tetszőleges évszakot, mi a valószínűsége annak, hogy abban egyetlen hónap középhőmérséklete sem lesz a több éves sor átlaga
a) felett
b) alatt?
Adott p = 0,5 valószínűségi alternatív esemény n esetből k-szori bekövetkezése milyen valószínűséggel várható.
Feladat típus:
Binomiális, mert p = 0,5
Meghatározzuk a Binomiális eloszlás paramétereit:
Paraméterek:
p = 0,5
n = 3;3
k = 0;3
Felírjuk a Binomiális eloszlás képletét:
n! k! ˇ (n - k)!
P(k ; n) = ˇ pk ˇ (1 - p) n-k
a)
P(0 ; 3) = ˇ 0,50 ˇ (1 - 0,5) 3-0
P(0 ; 3) = 0,125
(ha egy sincs az átlag felett)
P(3 ; 3) = ˇ 0,53 ˇ (1 - 0,5) 3-3
P(3 ; 3) = 0,125
(ha egy sincs az átlag alatt)
Válaszolunk a feladatra:
Tehát annak a valószínűsége, hogy egyetlen hónap:
középhőmérséklete sem lesz a több éves sor átlaga felett: 12,5%
középhőmérséklete sem lesz a több éves sor átlaga alatt: 12,5%
8.Feladat
Szombathelyen 140 év áprilisi középhőmérséklete 9,7°C, a szórás 2,3°C. Határozzuk meg az április középhőmérsékletek alsó és felső kvartilisét!
Mivel hőmérsékletről van szó, ezért Normál eloszlást alkalmazunk.
Meghatározzuk a Normális eloszlás paramétereit:
m = 9,7
σ = 2,3
F(dalsó) = 25,00% è d= - 0,678
F(dfelső) = 75,00% è d= 0,678
Grafikusan a feladat:
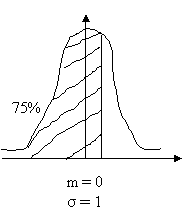
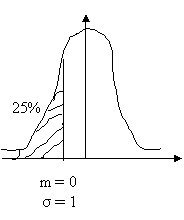
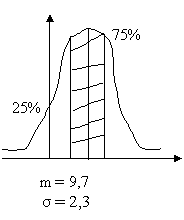
Oldjuk meg számszerűen:
x -
m
= d è x = d σ + m
Xalsó = - 0,678 ˇ 2,3 + 9,7 = 8,14
Xfelső = 0,678 ˇ 2,3 + 9,7 = 11,26
Válaszolunk a feladatra:
Tehát az áprilisi középhőmérsékletek
Alsó kvartilise: 8,14
Felső kvartilise: 11,26
9.Feladat
Szegeden a júniusi középhőmérséklete 20,4°C, a szórás 1,2°C. Határozzuk meg annak a számtani középre szimmetrikus intervallumnak az alsó és felső határát, amelybe normális eloszlás esetén 2/3 valószínűséggel esnek az értékek!
Mivel hőmérsékletről van szó, ezért Normál eloszlást alkalmazunk.
Meghatározzuk a Normális eloszlás paramétereit:
m = 20,4
σ = 1,2
F(dalsó) = ( 1 - 2/3 )/2 = 1/6 = 16,67% è d= - 0,97
F(dfelső) = ( 1 - 2/3 )/2 +2/3 = 5/6 = 83,33% è d= 0,97
Grafikusan a feladat:
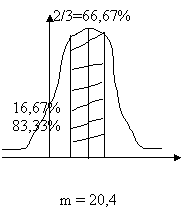
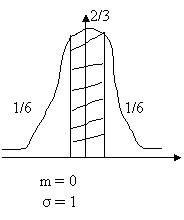
Oldjuk meg számszerűen:
x -
m
= d è x = d σ + m
Xalsó = - 0,678 ˇ 1,2 + 20,4 = 19,236
Xfelső = 0,678 ˇ 1,2 + 20,4 = 21,564
Válaszolunk a feladatra:
Tehát a júniusi középhőmérsékletek 2/3-os valószínűséggel esnek a
[ 19,236 ; 21,564 ] intervallumba.
10.Feladat
Hódmezővásárhelyen a 20 mm-t meghaladó napi csapadék átlagos gyakorisága 4 nap. Mi a valószínűsége annak, hogy egyszer sem fordul elő egy évbe és annak, hogy 5 alkalommal fordul elő egy évben 20 mm-t meghaladó napi csapadékösszeg.
Alapkérdés:
Adott p valószínűségi alternatív esemény n esetből k szori bekövetkezése milyen valószínűséggel várható.
Mivel az alapkérdést alkalmazhatjuk és p = = 0,01095 è p < 0,03 ezért a Poisson eloszlást alkalmazzuk.
Meghatározzuk a Poisson eloszlás paramétereit:
Paraméterek:
n ˇ p ; k
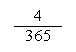
n ˇ p = 365 ˇ = 4
k = 0 ; 5
Felírjuk a Poisson eloszlás képletét:
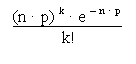
P(k ; n ˇ p) = e = 2,72
Behelyettesítünk a képletbe:
k = 0;5 ; n ˇ p = 4
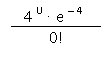
P(0 ; 4) =
P(0 ; 4) = 0,0183
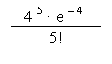
P(5 ; 4) =
P(5 ; 4) = 0,1562
Válaszolunk a feladatra:
Tehát annak a valószínűsége, hogy egy évben 20 mm-t maghaladó csapadék
0 alkalommal fordul elő: 1,83%.
5 alkalommal fordul elő: 15,62%.
11.Feladat
Budapest belterületén és külterületén 1975 júliusának és augusztusának 21 órai hőmérsékletei a következő módon oszlanak meg:
|
°C |
|
|
|
|
|
|
|
Belterület |
|
|
|
|
|
|
|
Külterület |
|
|
|
|
|
|
Kimutatható-e, hogy a külterülethez képest a belterület esti hőmérsékletei szignifikánsan eltérnek?
Nem mutatható ki szignifikáns eltérés a belterület és a külterület között.
Feladat típusa:
χ2 próba. Homogenitás vizsgálat.
A feltételezett értékek meghatározása ( az osztás közi gyakorisági értékeket )
|
°C |
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
Belterület |
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
Külterület |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1;1 = |
|
|
F2;1 = |
|
|
|
F1;2 = |
|
|
F2;2 = |
|
|
|
F1;3 = |
|
|
F2;3 = |
|
|
|
F1;4 = |
|
|
F2;4 = |
|
|
|
F1;5 = |
|
|
F2;5 = |
|
|
Végezzük el a χ2 próbát:
|
n i=1 |
( Éi - Fi ) Fi |
K= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( azért van kettővel szorozva, mert a sor/oszlop összegek megegyeznek így az F is )
K= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SzF = ( 2 - 1) ˇ ( 5 - 1 ) = 4
χ40,05 > K tehát a Null - hipotézis teljesül.
Válaszolunk a feladatra:
Tehát a Null - Hipotézis teljesül. Azaz: Nem mutatható ki szignifikáns eltérés a külterület és a belterület esti kőmérsékletei között (lényeges eltérést nem mutat).
12.Feladat
Egy ipari városban légszennyezettség-gátló berendezésekkel csökkentették a levegőbe jutó égéstermékek mennyiségét. A beavatkozás előtti 10 és a beavatkozás utáni 3 éven átvégzett megfigyelések szerint 13 órakor a jó, a közepes és rossz látástávolság az alábbi esetszámban volt megfigyelhető:
|
Látástávolság |
jó |
közepes |
rossz |
|
|
Beavatkozás előtt |
|
|
|
|
|
Beavatkozás után |
|
|
|
|
|
|
|
|
|
|
A Null - Hipotézis felvetése:
Nem mutatható ki lényeges eltérés a két minta között ( azaz nem mutatható ki a műszaki beavatkozás a város levegőjének tisztulásában )
Feladat típusa:
χ2 próba. Homogenitás vizsgálat.
A feltételezett értékek meghatározása ( az osztás közi gyakorisági értékeket )
|
Látástávolság |
jó |
közepes |
Rossz |
|
|
F |
|
|
|
|
|
Beavatkozás előtt |
|
|
|
|
|
F |
|
|
|
|
|
Beavatkozás után |
|
|
|
|
|
|
|
|
|
|
|
F1;1 = |
|
|
F2;1 = |
|
|
|
F1;2 = |
|
|
F2;2 = |
|
|
|
F1;3 = |
|
|
F2;3 = |
|
|
Végezzük el a χ2 próbát:
|
n i=1 |
( Éi - Fi ) Fi |
K= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SzF = ( 2 - 1) ˇ ( 3 - 1 ) = 2
χ20,05 < K tehát a Null - hipotézis nem teljesül.
Válaszolunk a feladatra:
Tehát a Null - Hipotézis nem teljesül. Azaz: Igen, kimutatható a műszaki beavatkozás a város levegőjének tisztulásában (a két minta lényeges eltérést mutat).
13.Feladat
Bresztben 60 év során a legcsapadékosabb évszakok megoszlása a következő volt:
|
Tél |
Tavasz |
Nyár |
Ősz |
|
|
|
|
|
Fenntartható-e az az állítás, hogy Bresztben a csapadékmaximum egyenlő eséllyel várható bármely évszakban?
A Null - Hipotézis feltevése:
A csapadékmaximum egyenlő várható bármely évszakban.
Feladat típusa:
χ2 próba. Tiszta illeszkedéses vizsgálat.
Határozzuk meg az F értékeket ( az osztás közi gyakorisági értékeket )
60/4 = 15 minden évszakra.
|
|
Tél |
Tavasz |
Nyár |
Ősz |
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
Végezzük el a χ2 próbát:
|
n i=1 |
( Éi - Fi ) Fi |
K= |
|
|
|
|
|
|
|
|
|
|
|
|
K= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SzF = ( 2 - 1) ˇ ( 4 - 1 ) = 3
χ30,05 > K tehát a Null - hipotézis teljesül.
Válaszolunk a feladatra:
Tehát a Null - Hipotézis teljesül. Azaz: A csapadékmaximum egyenlő eséllyel várható bármely évszakban. Igen, az állítás fenntartható.
14.Feladat
Sopronban az 1971 - 1975 közötti 5 év júniusi napjai közül 82 volt csapadékos. Adjunk 95%-os megbízhatósági becslést a csapadék valószínűségére júniusban!
Valószínűség konfidencia intervallum
|
p = |
|
|
( 54,7% ) |
|
|
n = 150
a választott valószínűségi szint 5% è d = 1,96
Oldjuk meg számszerűen a feladatot:
p = 0,547 ; n = 150 ; d = 1,96
|
σp = |
|
p(1 - p) |
|
|
|
|
|
|
|
|
n |
|
|
p1 = p - dσ = 0,547 - 1,96 ˇ 0,0406 = 0,467
p2 = p + dσ = 0,547 + 1,96 ˇ 0,0406 = 0,627
|
|
|
|
|
|
|
|
p1 = 0,467 |
p = 0,547 |
P2 = 0,627 |
|||
Válaszolunk a feladatra:
Tehát a 95%-os megbízhatósági becslés a csapadék valószínűségére
[P1 ; P2 ] = [ 0,467 ; 0,627] .
15.Feladat
Pécset 80 év megfigyelései alapján az augusztusi középhőmérséklet: 21,7°C, a szórás 1,3°C. Az értékek az alábbi módon oszlanak meg:
|
18-19°C |
19-20°C |
20-21°C |
21-22°C |
22-23°C |
23-24°C |
24-25°C |
|
|
|
|
|
|
|
|
Igazolható-e, hogy az adatok a normális eloszlás szerint oszlanak meg?
A Null - Hipotézis felvetése:
Nincs lényeges eltérés az adatok eloszlása és a normális eloszlás között.
Feladat típus:
χ2 próba. Becsléses illeszkedéses vizsgálat.
Paraméterek meghatározása:
A normális eloszlás paraméterei a minta paraméterei.
m = 21,7°C ; σ = 1,3°C
Normális eloszlást feltételezve határozzuk meg az F értékeket ( az osztás közi gyakorisági értékeket):
|
|
18-19;19-20°C |
20-21°C |
21-22°C |
22-23°C |
23-24;24-25°C |
|
|
Belterület |
|
|
|
|
|
|
|
Külterület |
|
|
|
|
|
|
|
x -m |
= d ; p = |
k |
→ k = p ˇ n ; n = 80 |
||
|
|
n |
||||
|
x = 20 → |
|
= - 1,31 = d → F(d) = 9,80% → p = 0,10; k = 0,10 ˇ 80 = 8 |
|||
|
x = 21 → |
|
= - 0,54 = d → F(d) = 29,19% → p = 0,29 - 10 = 0,19; k = 0,19 ˇ 80 = 15 |
|||
|
x = 22 → |
|
0,23 = d → F(d) = 58,00% → p = 0,58 - 0,29 = 0,29; k = 0,29 ˇ 80 = 23 |
|||
|
x = 23 → |
|
1,00 = d → F(d) = 84,13% → p = 0,84 - 0,58 = 0,26; k = 0,26 ˇ 80 = 21 |
|||
|
x = 24 → |
|
1,77 = d → F(d) = 96,41% → p = 0,96 - 0,84 = 0,12; k = 0,12 ˇ 80 = 10 |
|||
A maradék pedig: 80-8-15-23-21-10 = 3, ami a 24-25°C közötti
Végezzük el a χ2 próbát:
|
N i=1 |
( Éi - Fi ) Fi |
K= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SzF = ( 2 - 1) ˇ ( 5 - 1 ) = 4
χ40,05 > K tehát a Null - hipotézis teljesül.
Válaszolunk a feladatra:
Tehát a Null - Hipotézis teljesül. Azaz: Nincs lényeges eltérés a minta és a normális eloszlás között. Igen, igazolható, hogy az adatok a normális eloszlás szerinti oszlanak meg.
16.Feladat
Orosházán a megfigyelési sor alapján júliusban időszakban a 30°C fölötti maximum hőmérséklet bekövetkezési valószínűsége 30%. Két év során előfordult 21 anticiklonális időjárású július nap közül 14-en emelkedett a hőmérséklet 30°C fölé. Jelentősen befolyásolja-e az anticiklonális időjárás a nyári hőség kialakulását?
Nincs lényeges eltérés a 30°C fölötti maximum hőmérséklet bekövetkezési valószínűsége között, anticiklonális időjárású napokon és a szokásos között.
Valószínűség konfidencia intervallum.
Paraméterek meghatározása
P = 0,30 (30%)
|
p = |
|
|
( 67% ) |
|
|
n = 21
a választott valószínűségi szint 5% è d = 1,96
Oldjuk meg számszerűen a feladatot:
P = 0,30 ; p = 0,67 ; n = 21 ; d = 1,96
|
σp = |
|
p(1 - p) |
|
|
|
|
|
|
|
|
n |
|
|
p1 = p - dσ = 0,67 - 1,96 ˇ 0,103 = 0,47
p2 = p + dσ = 0,67 + 1,96 ˇ 0,103 = 0,87
Döntünk a Null - Hipotézis teljesülése ill. nem teljesülése között:
Nem igaz, hogy P [P1 ; P2 ] ezért a Null - Hipotézis nem teljesül.
|
|
|
|
|
|
|
|
|
|
|
P = 0,30 |
p1 = 0,47 |
p = 0,67 |
p2 = 0,87 |
|
||||
Válaszolunk a feladatra:
Tehát mivel P Ï [P1 ; P2 ] azaz 0,30 Ï [ 0,47 ; 0,87 ] ezért a Null - Hipotézis nem teljesül. Azaz az anticoklonális időjárású napokon a 30°C fölötti maximum hőmérséklet bekövetkezési valószínűsége a szokásostól lényegesen eltér (nagyobb). Igen, jelentősen befolyásolja az anticiklonális időjárás a nyári hőség kialakulását.
17.Feladat
Siófokon 10 év összes júniusi napja közül 75-ön jegyeztek fel 10 m/s-nál nagyobb széllökést. Ugyanezen időszak 60 zivataros napja közül 33-on fordult elő ekkora értékű szélsebesség. Kimondható-e, hogy zivataros napokon jelentősen nagyobb az erős szél bekövetkezési valószínűsége?
Nincs lényeges eltérés az erős szél csapadék bekövetkezési valószínűsége között Siófokon júniusban, a zivataros napokon és a szokásos között.
Valószínűség konfidencia intervallum.
Paraméterek meghatározása:
|
P = |
|
|
( 25% ) |
|
|
|||
|
p = |
|
|
( 55% ) |
|
|
n = 60
a választott valószínűségi szint 5% è d = 1,96
Oldjuk meg számszerűen a feladatot:
P = 0,25 ; p = 0,55 ; n = 60 ; d = 1,96
|
σp = |
|
p(1 - p) |
|
|
|
|
|
|
|
|
n |
|
|
p1 = p - dσ = 0,55 - 1,96 ˇ 0,064 = 0,42
p2 = p + dσ = 0,55 + 1,96 ˇ 0,064 = 0,68
Döntünk a Null - Hipotézis teljesülése ill. nem teljesülése között:
Nem igaz, hogy P [P1 ; P2 ] ezért a Null - Hipotézis nem teljesül.
|
|
|
|
|
|
|
|
|
|
|
P = 0,25 |
p1 = 0,42 |
p = 0,55 |
p2 = 0,68 |
|
||||
Válaszolunk a feladatra:
Tehát mivel P Ï [P1 ; P2 ] azaz 0,25 Ï [ 0,42 ; 0,68 ] ezért a Null - Hipotézis nem teljesül. Azaz az zivataros napokon az erős szél bekövetkezési valószínűsége a szokásostól lényegesen eltér (nagyobb az erős szél bekövetkezési valószínűsége). Igen, kimutatható, hogy zivataros napokon jelentősen nagyobb az erős szél bekövetkezési valószínűsége.
18. Feladat
San Cristobal (Galápagosz-szg) megfigyelő helyen az átlagosnál csapadékosabb március bekövetkezési valószínűsége 46%. 11 olyan márciusi hónapból, amikor a környező tenger vizének hőmérséklete legalább 1°C-al melegebb volt a szokásosnál, 8 volt az átlagosnál csapadékosabb. Igazolható-e, hogy meleg tenger környezetében a szokásosnál több a csapadék?
Nincs lényeges eltérés az erős szél csapadék bekövetkezési valószínűsége között akkor, amikor a környező tenger hőmérséklete legalább 1°C -al melegebb és a szokásos között.
Valószínűség konfidencia intervallum.
P = 0,46 (46%)
|
p = |
|
|
( 73% ) |
|
|
n = 11
a választott valószínűségi szint 5% è d = 1,96
Oldjuk meg számszerűen a feladatot:
P = 0,46 ; p = 0,73 ; n = 11 ; d = 1,96
|
σp = |
|
p(1 - p) |
|
|
|
|
|
|
|
|
n |
|
|
p1 = p - dσ = 0,73 - 1,96 ˇ 0,134 = 0,47
p2 = p + dσ = 0,73 + 1,96 ˇ 0,134 = 0,99
Döntünk a Null - Hipotézis teljesülése ill. nem teljesülése között:
Nem igaz, hogy P [P1 ; P2 ] ezért a Null - Hipotézis nem teljesül.
|
|
|
|
|
|
|
|
|
|
|
P = 0,46 |
p1 = 0,47 |
p = 0,73 |
p2 = 0,99 |
|
||||
Válaszolunk a feladatra:
Tehát mivel P Ï [P1 ; P2 ] azaz 0,46 Ï [ 0,47 ; 0,99 ] ezért a Null - Hipotézis nem teljesül. Azaz amikor a környező tenger hőmérséklete legalább 1°C-al melegebb és a szokásosnál, akkor a csapadék valószínűsége a szokásosnál több. Igen, igazolható, hogy meleg tenger környezetben a szokásosnál több csapadék.
19. Feladat
Budapesten az átlagosnál csapadékosabb január bekövetkezési valószínűsége 46%. 14 átlagosnál hidegebb január közül 9 volt az átlagosnál csapadékosabb. Kimondható-e, az információk alapján, hogy a hidegebb januárok a szokásosnál csapadékosabbak?
Nincs lényeges eltérés az átlagosnál csapadékosabb január bekövetkezési valószínűsége között akkor, amikor az átlagosnál hidegebb január van és a szokásos között.
Valószínűség konfidencia intervallum.
P = 0,46 (46%)
|
p = |
|
|
( 64% ) |
|
|
n = 14
a választott valószínűségi szint 5% è d = 1,96
Oldjuk meg számszerűen a feladatot:
P = 0,46 ; p = 0,64 ; n = 14 ; d = 1,96
|
σp = |
|
p(1 - p) |
|
|
|
|
|
|
|
|
n |
|
|
p1 = p - dσ = 0,64 - 1,96 ˇ 0,145 = 0,36
p2 = p + dσ = 0,64 + 1,96 ˇ 0,145 = 0,92
Döntünk a Null - Hipotézis teljesülése ill. nem teljesülése között:
Nem igaz, hogy P [P1 ; P2 ] ezért a Null - Hipotézis teljesül.
|
|
|
|
|
|
|
|
|
|
|
p1 = 0,36 |
P = 0,46 |
p = 0,64 |
p2 = 0,92 |
|
||||
Válaszolunk a feladatra:
Tehát mivel P [P1 ; P2 ] azaz 0,46 [ 0,36 ; 0,92 ] ezért a Null - Hipotézis teljesül. Azaz: Nincs lényeges eltérés az átlagosnál csapadékosabb január bekövetkezési valószínűsége között akkor, amikor az átlagosnál hidegebb január van és a szokásos között. Nem mondható ki az információk alapján, hogy a hideg januárok a szokásosnál csapadékosabbak.
20. Feladat
Békéscsabán 80 évi megfigyelés alapján az októberi középhőmérséklet: 12,4°C, a szórás 1,4°C. Az adatok gyakorisági eloszlása a következő:
|
7-8°C |
8-9°C |
9-10°C |
10-11°C |
11-12°C |
12-13°C |
13-14°C |
14-15°C |
15-16°C |
16-17°C |
|
|
|
|
|
|
|
|
|
|
|
Igazolható-e, hogy az adatok a normális eloszlása?
A Null - Hipotézis felvetése:
Nincs lényeges eltérés az adatok eloszlása és a normális eloszlás között.
Feladat típus:
χ2 próba. Becsléses illeszkedéses vizsgálat.
Paraméterek meghatározása:
A normális eloszlás paraméterei a minta paraméterei.
m = 12,4°C ; σ = 1,4°C
Normális eloszlást feltételezve határozzuk meg az F értékeket ( az osztás közi gyakorisági értékeket):
|
|
7-8-;8-9;9-10;10-11°C |
11-12°C |
12-13°C |
13-14°C |
14-15;(15-16;16-17)°C |
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
x -m |
= d ; p = |
k |
→ k = p ˇ n ; n = 80 |
||
|
|
n |
||||
|
x = 11 → |
|
= - 1 = d → F(d) = 15,87% → p = 0,16; k = 0,16 ˇ 80 = 13 |
|||
|
x = 12 → |
|
= - 0,29 = d → F(d) = 38,265% → p = 0,38 - 16 = 0,22; k = 0,22 ˇ 80 = 18 |
|||
|
x = 13 → |
|
0,43 = d → F(d) = 65,54% → p = 0,66 - 0,38 = 0,28; k = 0,28 ˇ 80 = 22 |
|||
|
x = 14 → |
|
1,14 = d → F(d) = 87,4% → p = 0,87 - 0,66 = 0,21; k = 0,21 ˇ 80 = 17 |
|||
|
x = 15 → |
|
1,86 = d → F(d) = 96,61% → p = 0,97 - 0,87 = 0,10; k = 0,10 ˇ 80 = 8 |
|||
A maradék pedig: 80-13-18-22-17-8 = 2, ami a 15-17°C közötti
Végezzük el a χ2 próbát:
|
n i=1 |
( Éi - Fi ) Fi |
K= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SzF = ( 2 - 1) ˇ ( 5 - 1 ) = 4
χ40,05 > K tehát a Null - hipotézis teljesül.
Válaszolunk a feladatra:
Tehát a Null - Hipotézis teljesül. Azaz: Nincs lényeges eltérés a minta és a normális eloszlás között. Igen, igazolható, hogy az adatok a normális eloszlás szerinti.
Találat: 7295
