| kategória | ||||||||||
|
|
||||||||||
|
|
||
A kép és a képfeldolgozó, mint fizikai valóság
A hardver
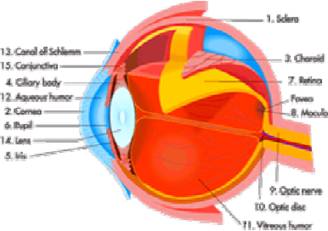 Az emberi szem:
Az emberi szem:
sclera: stabil alaktartás
choroid: vérellátás
ciliary body: lencse szabályozása
cornea: fénytörésért felelős
lens: közeli éles látás
a szemgolyó és
a cornea mögötti
rész folyadékkal telített.
iris: közepe a pupilla, apertura
iris: minél kevesebb pigment -> kék szem
retina:
rod (pálcikák)
cone (csapok)
fovea
optic nerve 838h75i
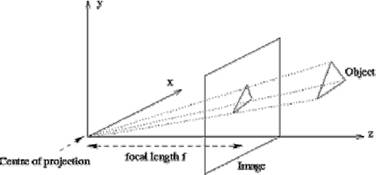
"Pinhole" kamera modell
legegyszerűbb kamera modell
perspektivikus projekció
Omni vision


Panoráma képek
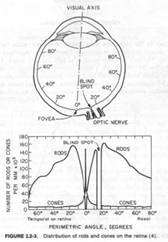 Csapok és pálcikák
Csapok és pálcikák
vakfolt
optikai kivezetés
800.000 idegszál
scotopic vision:
alacsony fény
pálcikák (100-120 millió)
photopic vision:
erős fény
csapok (7 millió)
Pálcikák
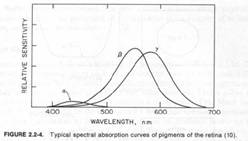
három fő típus
a kék
érzékelők relatív
érzékenysége alacsonyabb
jelentős átlapolódás
A retina szerkezete
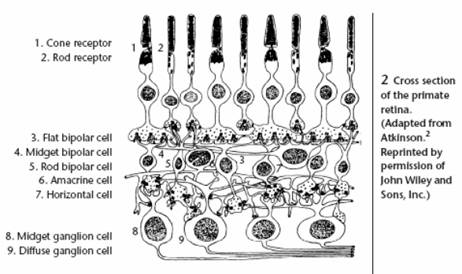
Receptív mező, előfeldolgozás
receptív mező: adott ganglionhoz tartozó fotoreceptorok
egyenletes stimuláció a receptív mezőn: gyenge válasz
receptív mező közepe: erősítés
körkörösen: gátlás
X/Y ganglionok: hosszantartó reakció az időben / erős tranziens
on-center/off-center sejtek: fény növekedésére vagy csökkenésére
növekszik a sejt intenzitása
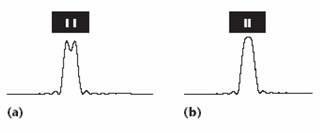 Éles látás
Éles látás
max. felbontóképesség:
hyperacuity:
Fényérzékelés és adaptáció
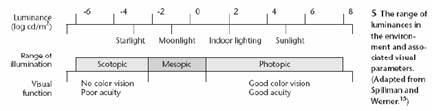
lencserendszer
receptorok
neurális feldolgozás
Kontraszt érzékenység
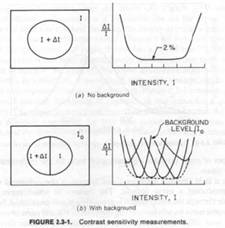
a szem
nem-linárisan reagál
az intenzitásváltozásra
∆l: éppen érzékelhető kontraszt
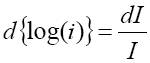
Speciális kontraszt effektusok
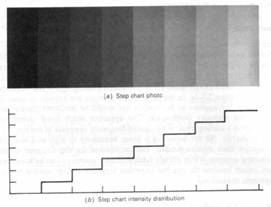 match band
effect: homogén sáv
match band
effect: homogén sáv
nem tűnik homogének
szimultán kontraszt: a középső
négyzetek intenzitása azonos

White's illusion Kontraszt érzékenység


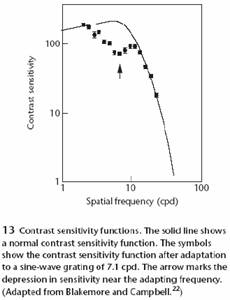 Kontraszt érzékenység adaptációja
Kontraszt érzékenység adaptációja

Látási rendellenességek
monochromats: nincs, vagy csak egyféle pálcika
dichromats: kétféle pálcika
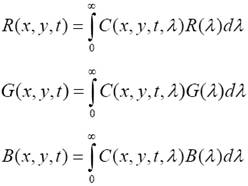
Kép mint folytonos 2D függvény
C(x,y,t,λ):
képforrás sugárzó
energiájának eloszlása
![]()
Különbségi operátorok
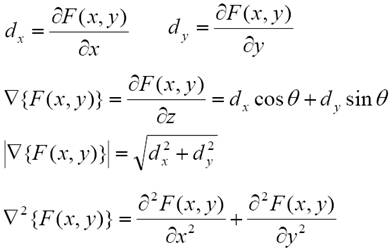
Kép-reprezentáció
pixelek
MxN pixel - MxN mátrix - x,y tengelyek
![]() szomszédságok (4, 8)
szomszédságok (4, 8)
távolságok - Euklideszi:
volume element: voxel
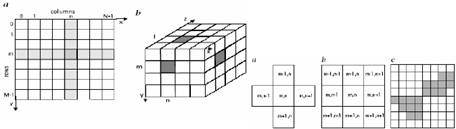
Hisztogramok
kép színeinek statisztikája
információ a
kép minőségéről, láthatóságáról, színtartalmáról
(keskeny: kis kontraszt, két púp: előtér/háttér, stb.)
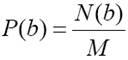 belőle is lehet alapvető mérőszámokat származtatni:
belőle is lehet alapvető mérőszámokat származtatni:
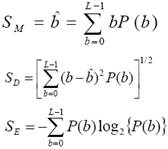
átlag:
szórás:
entrópia:
Hisztogram-transzformációk

 széthúzás
(stretching)
széthúzás
(stretching)
Look-Up Table (LUT) generálás:
lineáris:
o négyzetes (sötétít)
o gyökös (világosít)
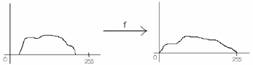 nem-lineáris
nem-lineáris
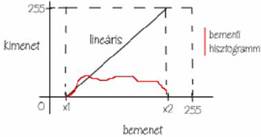

hisztogram-kiegyenlítés
(equalize):
o nem-adaptív
o adaptív
o
célja: a
kontraszt
növelése
Fourier transzformáció
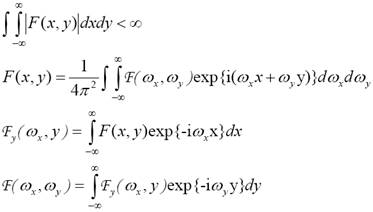
Operátorok:
lineáris - deriválás
skálázás - 2. derivált
konvolúció - 2D FT
parzevál egyenlőség - operátorok az FT tulajdonságai
autokorrelációs tulajdonság - pixelek, voxelek, Jahne
derivált - hisztogram, hisztogram-transzformációk
Képalkotás
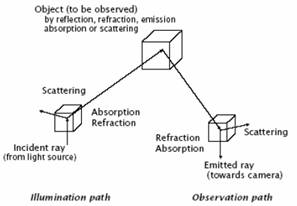 Kvantitatív
vizualizáció
Kvantitatív
vizualizáció
sugárzás: elektromágneses
vagy akusztikus
Fő kérdések:
Sugárzás típusai
elektromágneses
részecske sugárzás
akusztikus
Mindhárom hullámformában terjed, alapvető tulajdonsága a hullámhossz, ami meghatározza, hogy mekkora objektumokat tudunk mérni.

Elektromágneses sugárzás
C = 3x108 ms-1
C = λ . ν (hullámhossz [Hz] x frekvencia [1/s])
egymásra és a haladás irányára merőleges elektromos és mágneses mező váltakozása
Elektromágneses sugárzás kölcsönhatásai
töltéssel, árammal, mágneses és elektromos mezővel
refrakciós index: η = n + i Χ
n: sebesség csillapítás (c/u)
X: amplitúdó csillapítás
a refrakciós index függ az elektromágneses hullám frekvenciájától (hullámhosszától)
hullám sebessége függ a hullámhossztól à diszperzió
Vegyi anyagok optikai analízise
refrakciós index: η = n + i Χ
n: sebesség csillapítás (c/u)
amplitúdó csillapítás
Elektromágneses sugárzás
linearitás: komplex hullámok lebonthatók síkbeli harmonikus hullámokra; két hullám szuperpozíciója is em. hullám lesz
nemlineáris jelenségek: pl. nagyon erősen koncentrált fény: lézer
polarizáció: általában az EM hullámok nem polarizáltak
koherencia: ha a fázisuk közt véletlenszerű kapcsolat van, akkor inkoherens a két sugár, ellenkező esetben koherensek a sugarak
koherens sugarak kioltják egymást a 180o-os fáziseltolásoknál
a természetben előforduló fény inkoherens, a lézer koherens
Fotonok
EM sugárzásnak részecske tulajdonsága is van!
az EM energia egy kvantuma a foton
EM energia kvantált: E = h . ν (Planck állandó x frekvencia)
eV = foton mozgási energiája 1 Volt gyorsítás után
a foton számlálók 1 foton becsapódását is képesek érzékelni
Részecske sugárzás
mivel nyugalmi tömegük van, ezért a fénynél lassabban mozognak
fotonhoz hasonló terjedési tulajdonságok jellemzik: hullámszerű terjedés, E = h . ν
alfa (kétszeres pozitív töltés)
béta: elektron-sugárzás
proton
neutron
Elektron: 20keV à λ=10-11m, ami kisebb az atom átmérőjénél à elektron mikroszkóp
Hanghullámok
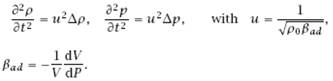 hordozóra van szükség
hordozóra van szükség
longitudinális hullámok
o ρ: sűrűség,
o ρ0: statikus sűrűség, A sebesség nem függ
o P: nyomás, u sebesség a frekvenciától!
levegő: 344 m/s
víz: 1485 m/s
vas: 5100 m/s
Ultrahang mikroszkópia: nagy frekvencia, μm hullámhossz.
Képalkotás
geometriai aspektusok 3D - 2D projekció, 3D képalkotás
radiometria a képen reprezentált világosság hogyan függ az objektum optikai tulajdonságaitól, a mérési módszertől?
mintavétel, digitalizálás
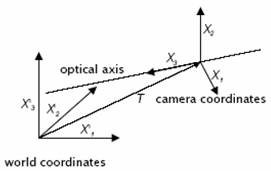
Koordináta rendszerek
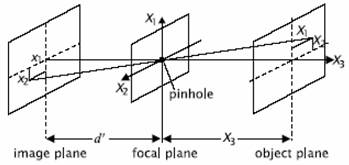
Ideális kamera modellek
"Pinhole" kamera:
perspektívikus projekció
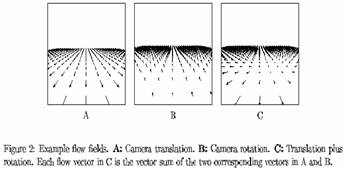
Képpontok mozgása
a kamera képén
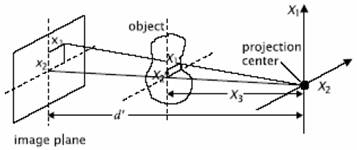
Röntgen
képalkotás
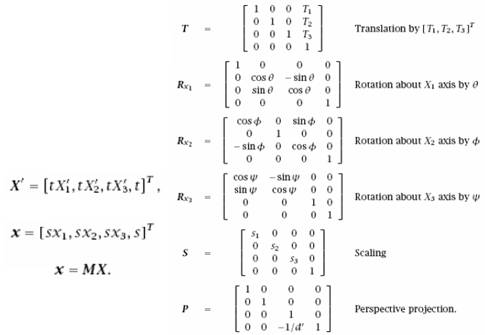
Homogén
koordináták
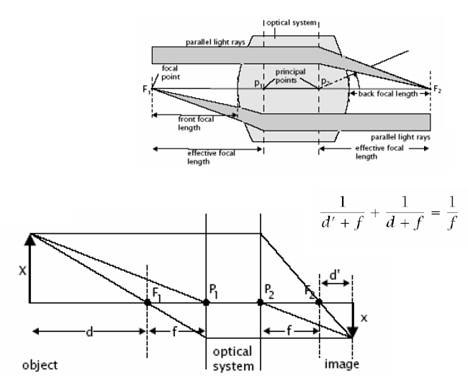
Valós
képalkotás
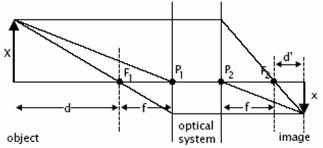 Valós
képalkotás
Valós
képalkotás
axiális nagyítás: ma
laterális nagyítás: ml
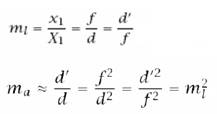
Elmosás (blur)
Hibás képtávolságból (nem lencse hibából adódóan) - lásd fixfókuszos kamerák
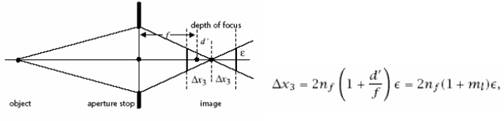
Depth of Focus
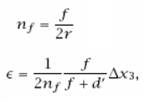
F érték:
Elmosás sugara:
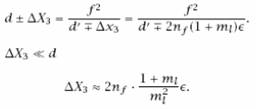 Elmosás
rossz tárgytávolságból
Elmosás
rossz tárgytávolságból
depth of field
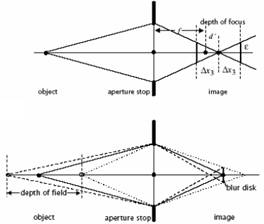
Pl. CCD pixelméret: 10μm x 10μm
εmax = 5μm (megengedett, f = 15mm,
nf = 2, d = 1.5m, ΔX=0.2m (depth of field))
Mikroszkópia: ml = 50, nf = 2,
ΔX = 0.2μm
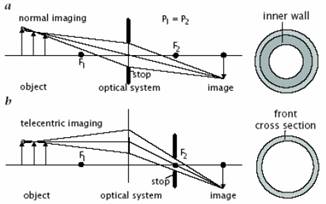 Telecentrikus képalkotás
Telecentrikus képalkotás
nagyméretű optikát igényel
(tárggyal összemérhető)
Lencsehibák
szférikus aberráció
kóma
asztigmatizmus: különböző síkok mentén más a nagyítás, kör alakú tárgy képe oválisnak képződik le
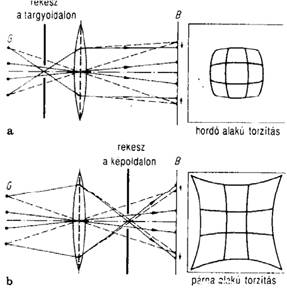
párna és hordótorzítás
képmezőgörbület: sík tárgyat görbült felületen képez le az optika
Szférikus aberráció
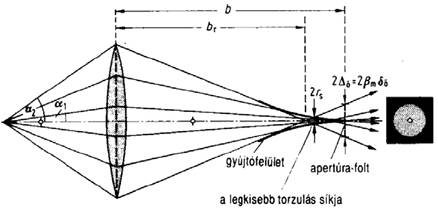
Kóma
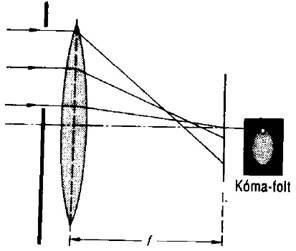
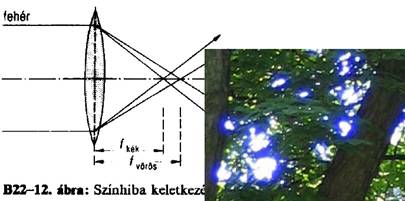
Kromatikus
aberráció

F 2.0 F 8.0
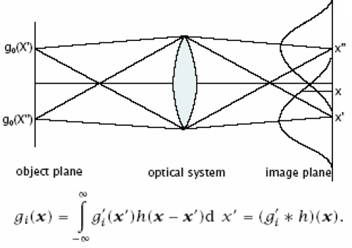
PSF
(Point Spread Function)
OTF (Optical Transfer Function)
A PSF Fourier transzformáltja

Diffraction-limited optical systems
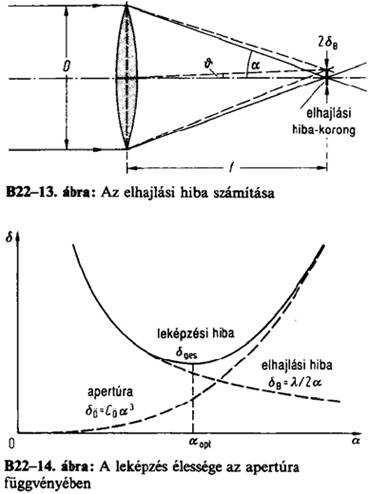
ha az optikai hibákat mind kiküszöböljük, akkor is tapasztalható elmosódás a képen
az elmosódás összemérhető a hullámhosszal
Frauenhofer diffrakció (elhajlás): modell síkhullám törésére aperturánál
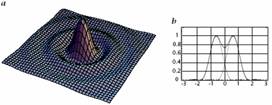 Airy
disk
Airy
disk
a középső pont az energia
83.9%-át képviseli
![]() Rayleigh kritérium
Rayleigh kritérium
(a középpont és az első
gyűrű távolsága):
3D-s képalkotás
![]() depth imaging
depth imaging
volumetric imaging
fő jellemzőjük:
Módszerek
távolság háromszögelésből (geodézia, térképészet), structure from motion
távolság a visszaverődési idő függvényében
interferometria: a sugárzás amplitúdóján kívül a fázisát is mérik - erősítések, kioltások, kb. 10-9m felbontás
távolság több projekcióból: tomográfia
Éldetekció
Célja, főbb szempontok
változások detektálása
differencián alapul
többdimenziós képeken is.
az él erőssége is fontos!
konvolúcióval vagy Fourier térben szorzással számolható

Célja
képi információk, struktúra kinyerése
o sarkok, vonalak, határok
o alkalmazási területek
o szegmentálás
o karc-szűrés
o felismerések
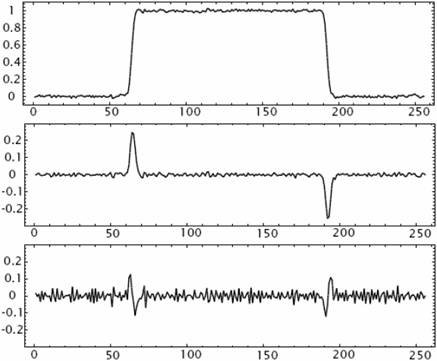
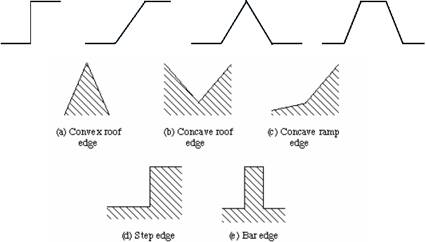 Típusok
Típusok
lépcső, rámpa, háztető, vonal
(step, ramp, roof, line)
SNR: magasság/zajszórás
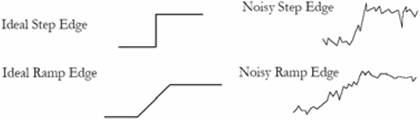
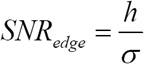
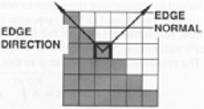 Tulajdonságok
Tulajdonságok
normális: vektor, ami merőleges az élre és a
legnagyobb intenzitásváltozás irányába mutat
irány: a vonal irányába mutató vektor
helyzet, középpont
erősség: intenzitásának aránya a környező kontraszttal
Főbb problémák
anizotróp detekció: a detekció nem működik minden irányban azonosan
az irányok becslése pontatlan
Tulajdonságok
![]()
gradiens vektor:
![]()
gradiens nagysága:
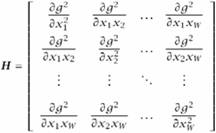
Hesse-mátrix:
![]() Laplace operátor:
Laplace operátor:
Zero Shift: az operátor pontos helyen kell, hogy detektáljon: szimmetrikus
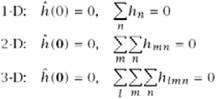
konstans függvényen 0-t kell jeleznie:
Gradiens alapú detekció
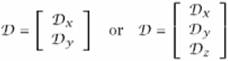
a gradiens vektor
maximumát keressük:
![]()
magnitúdó:
![]()
gyors változat:
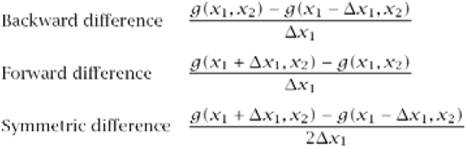
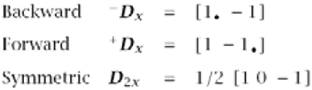
Laplace alapú detekció
![]() Fourier térben:
Fourier térben:
![]() Pixel tartományban:
Pixel tartományban:
![]() 2D esetben:
2D esetben:
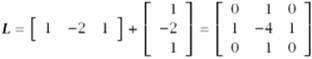
 Példák
Példák
|
Bemenet |
Laplace |
|
Gradiens X |
Gradiens Y |
|
Magnitúdó |
|
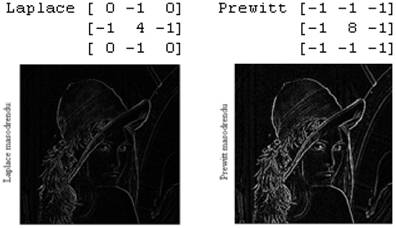
 Prewitt
és Sobel
Prewitt
és Sobel
átlagoló élszűrők:

Laplace és másodrendű Prewitt
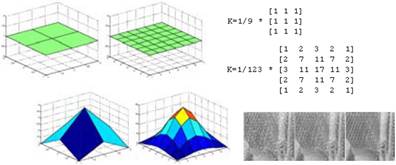
LoG, DoG
Laplace of Gaussian
Derivative of Gaussian
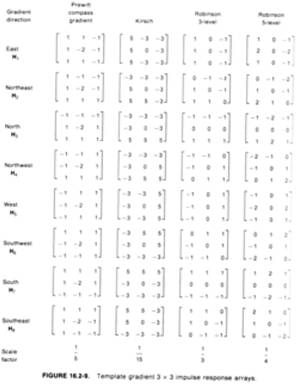
Compass
max[D1,D2,D3.]
Kirsch - Compass

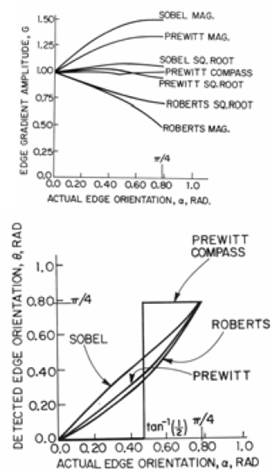
Éldetekció hibái
![]()
jó detekció valószínűsége:
![]()
hibás detekció valószínűsége:
![]() döntési hiba:
döntési hiba:
![]()
t helyes megválasztása:
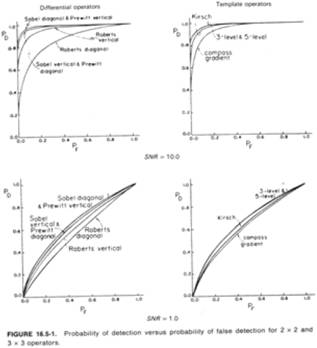
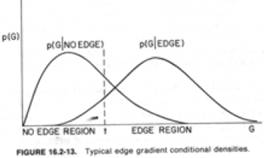
 Összehasonlítás
Összehasonlítás
Élek erősítése
él-erősítő maszkok

 Wallis szűrő
Wallis szűrő

Szűrések frekvencia tartományban
zajszűrések
o alul-áteresztő szűrés
él-kiemelések
o felül-áteresztő szűrés
2D-s transzformációk
Alkalmazási területek
tulajdonság kiemelés (pl. DC FT együttható)
tömörítés: együtthatók kvantálhatók, bizonyos együtthatók elhagyhatók
szűrés: dimenzió-csökkentés után kevesebb számítással elvégezhető
Unitér transzformációk
invertálható, lineáris transzformációk (U) véges dimenziós térben (V), ahol a kernel bizonyos ortogonális tulajdonsággal rendelkezik
ekvivalens állítások:
o
![]() U unitér
U unitér
o a belső szorzatot megtartja:
o UU*T = I
o U sorai ill. oszlopai ortonormált bázist alkotnak
![]() Fontos
tulajdonságok:
Fontos
tulajdonságok:
norma tartó tulajdonság:
o f vektor formula, F mátrix formula transzformáció: f = A f
o inverz transzformáció: f = B f
o B = A-1 (A-1 = A*T)
o ha A = AT akkor A ortogonális
ha A szeparálható, akkor a transzformáció elvégezhető soronként, majd oszloponként:
o A = AC X AR (X külső szorzat)
o F = ACFATR , F = BCFBTR
Fontos transzformációk
Fourier
koszinusz, szinusz, Hartley
Hadamard, Haar, Slant
Karhunen-Loeve
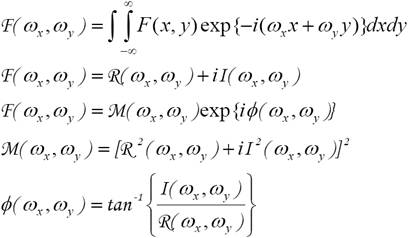
Fourier
transzformáció
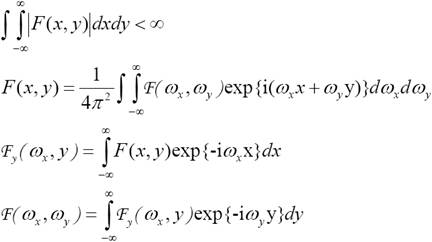
lineáris, skálázás, konvolúció ,Parzevál
egyenlőség,
autokorrelációs tulajdonság ,derivált


Diszkrét 2D Fourier transzformáció
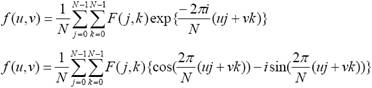
a transzformáció:
j , k : térbeli koordináták
u , v : frekvencia koordináták
![]()
f(0,0) a kép átlagértékéről hordoz információt:
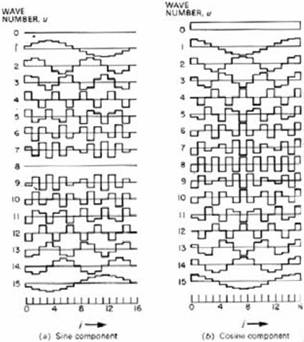
Fourier transzformáció
bázis függvény
Diszkrét 2D Fourier transzformáció
![]()
a transzformáció:
![]()
az inverz transzformáció:
![]()
szeparálható:
DFT: periodikus
amennyiben n és m egész:
![]()
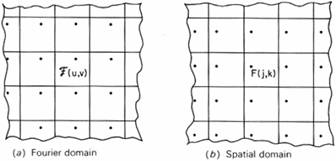
következmény:
![]()
A Fourier spektrum periodikus, csakúgy mint a tér spektrum (mivel a transzformáció tekinthető egy Fourier sorba fejtésnek, ennek pedig a jel periodikussága a feltétele).
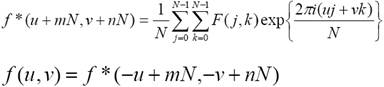 Konjugált szimmetria:
Konjugált szimmetria:
ahol m,n = 0, à tehát csaknem a spektrum fele redundáns

DFT vizualizációja
DFT-nek nagyobb a dinamikája,
mint magának a képnek
megjelenítés során a
transzformációs
együtthatókat szaturálni kell, vagy
logaritmikus függvényt használni
D(u,v) = log( a + b |f(u,v)| )
DFT összegzés
mivel komplex együtthatói vannak, így nehéz tömöríteni
elsősorban analízisre és digitális szűrésre használható
a Fourier transzformáció gyenge konvergenciája, a kép szélein lévő (a kép tartalmától természetesen függő) "ugrások" következménye
gyors algoritmus: FFT
PSF (Point Spread Function)
![]()
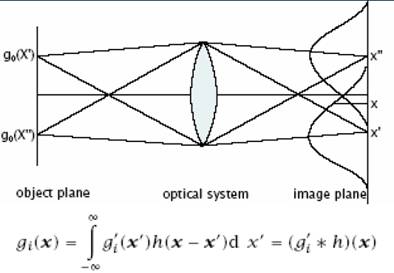
OTF (Optical Transfer Function)
a PSF Fourier transzformáltja

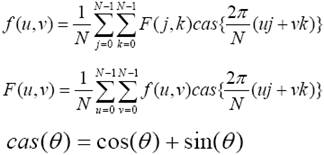 Hartley
transzformáció
Hartley
transzformáció
hasonló tulajdonságai vannak,
mint a DFT-nek, de bizonyos
esetekben gyorsabban lehet
implementálni
Koszinusz transzformáció
a képet tükrözzük -½ , -½ pontok körül
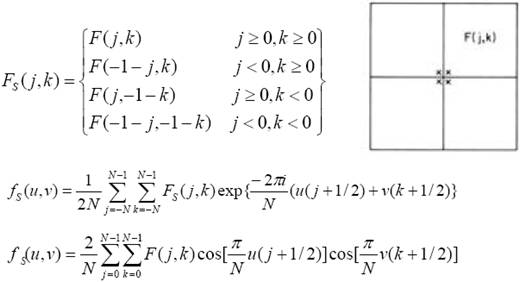
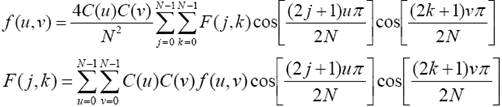
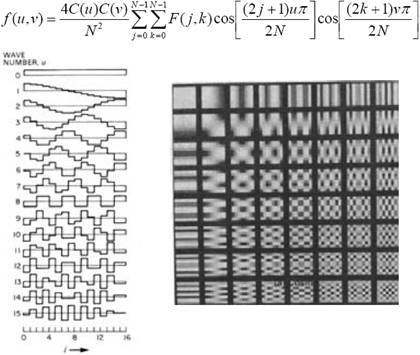
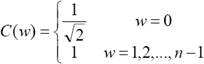
nem egyszerűen a DFT szinuszos komponenseinek elhagyásával kapható, hanem a kép tükrözése alapján, annak Foruier transzformációja, egyszerűsítések és normálás után kapjuk
a tükrözés miatt nem reprezentál implicit magas frekvenciás ugrásokat a kép széleinél, emiatt nagyobb az energiatömörítési képessége, több együttható hagyható el kevés veszteség mellett
FFT-vel számolható
nagyon jó tömörítésre
Walsh-Hadamard
Hadamard mátrixokon alapul, aminek a sorai és oszlopai ortogonálisak
![]() HHT = I
HHT = I
legkisebb ortonormált mátrix:
![]()
a Hadamard mátrixok rekurzív képzési szabálya:
bináris bázisfüggvények:
![]()
o
![]() bázisképek a Hadamard
bázisképek a Hadamard
mátrix soraiból ill. oszlopaiból képezve
komplexitása: n * log n
 egyszerű implementációja miatt kedvelt,
egyszerű implementációja miatt kedvelt,
mivel nem szükséges szorzást számolni
a 1 értékek miatt
sequency: a mátrix soraiban történő
előjelváltozások száma osztva 2-vel
a mátrix sorai ún. Walsh
függvények
által generálhatók à Walsh-Hadamard
transzformáció
sequency tulajdonság: jelváltozások
száma soronként nő
H Hadamard transzformáció valós,
szimmetrikus, ortogonális: H = H* = HT = H-1
Haar transzformáció

különböző frekvenciájú mintavételnek felel meg à Wavelet transzformáció
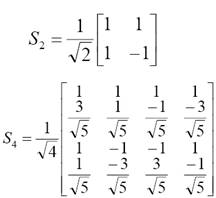 Slant
transzformáció
Slant
transzformáció
fix bázisfüggvények
Slant bázisok
sequency tulajdonság
gyorsan számítható
jól tömörít
 Példa
Példa
Karhunen-Loeve transzformáció (KLT)
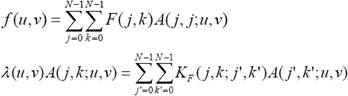
K: a kép kovarianciája
A: sajátfüggvény
λ: sajátérték
optimális a kép energiájának tömörítése szempontjából
adaptív: függ a kép méretétől és tartalmától, a bázisfüggvényeket a kép kovarianciájából kell kiszámolni
bonyolult kiszámítani, nem lehet analitikusan explicit kiszámolni a bázisvektorokat, iteratív módszer használható.
EPE: Energy Packing Efficiency
ahol X-ek a transzformált együtthatók, M≤N (pl. N=8, M=4)
a) DCT
b)
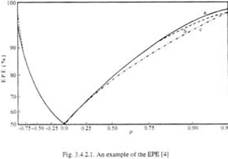 KLT, (ρ=0.36 korrelációs együtthatójú,
KLT, (ρ=0.36 korrelációs együtthatójú,
First Order Markov Process-re optimalizált
KLT bázisfüggvényekkel számolva)
c)
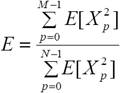 DFT
DFT
Találat: 5717