A NOETHER-TÉTEL LEVEZETÉSE

A NOETHER-TÉTEL LEVEZETÉSE

Hogy megérthessük Noether módszerét, először az energiamegmaradás egyenletét fogjuk megvizsgálni olyan esetben, amikor a rendszer Lagrange­függvénye nem függ explicit módon a t időtől. Ezért a t független változót a következő transzformációval visszük át:

t = t'+a

ahol a infinitezimális állandó. Most a variációs probléma q_i(t) változója megváltozik ennek a transzformációnak hatására, de úgy is vizsgál­hatjuk, mint t' függvénye, és így elhagyjuk az előző t változót. Ekkor a Lagrange-függvényünk a következő formájú lesz:

L = L q_i q_i', t a

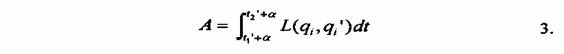Tételezzük fel azonban, hogy a Lagrange-függvény nem függ explicit módon a t időtől. Ekk 838i84i or az új variációs integrál alakja a következő lesz:

Így látni fogjuk, hogy az a konstans nem jelenik meg a variációs integ­rálban, csak a határoknál. Noether ezeket a variációs problémákat vizsgálta.

Most általánosítjuk a vizsgálatot, és többé nem tesszük fel, hogy a ál­landó, és a-t a t' függvényeként vizsgáljuk, amely kielégíti a következő pe­remfeltételeket:

a (t₁)=a (t₂ =0

Ebben az esetben a hatásintegrál az a'(t') függvénye lesz, de csak a'(t') jelenik meg explicit módon az integrálban. Ezért most a következő­képpen írhatjuk fel az általános koordinátákat:

és a transzformált probléma Lagrange-függvénye a következő lesz (tekin­tetbe véve a(t') infinitezimális természetét):

Továbbá

dt = a )dt'    7.

Így az új variációs integrálunk alakja a következő lesz (elhagyva a(t') magasabb rendű deriváltjait):

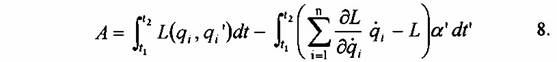
Így az 1. számú transzformáció nem változtatja meg a variációs problé­mát, és nem várhatjuk azt, hogy a hatásintegrál új formája több informáci­ót ad, mint az előző alak. Ebben a 8. számú egyenletben megadott forma esetén egy újabb szabadsági fok áll rendelkezésünkre, azaz a(t'), amelyet az előző általános koordinátához q_i(t')-hoz adtunk. Így az a(t')-höz tar­tozó Lagrange-egyenlet a következő alakú lesz:

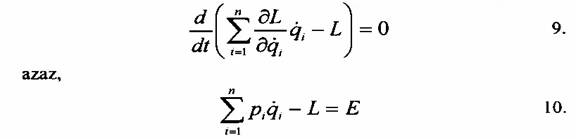ami a klasszikus mechanika jól ismert energiamegmaradási tétele. Ez nem egy újabb egyenlet, amit a Lagrange-egyenleteken kívül kell még kezelni, hanem a Lagrange-egyenletek következménye. Ezt a Noether-féle transz­formációs törvénybál következtettük ki, ami a variációs integrált változat­lanul hagyja. Meg kell jegyezni és nagyon fontos, hogy a Lagrange-függ­vény létezéséhez potenciálos erőterek szükségesek, és hallgatólagosan feltételeztük, hogy potenciálos erőterek hozzák létre a mozgást. Ezért ál talános esetben ez a gondolatmenet csak potenciálos erőterekre érvényes, amit nem szoktak külön hangsúlyozni.

Az előző példát az időbeli eltolás invarianciájaként foghatjuk fel, hi­szen az időt, mint változót transzformáltuk infinitezimális módon, kis mértékben. Így tehát az energia az idő mentén történő eltolásnak vagy szimmetria-transzformációként fogható föl.

Így jutottunk először 1918-ban az energia fizikai természetének meg­értéséhez, legalábbis potenciálos, konzervatív erőterek esetén. Ekkor azonban az energiamegmaradás tétele már mélyen gyökerezett a kutatók­ban, ekkor már természetesnek vették, hogy az energia minden körülmé­nyek között állandó. Ugyanez történt a mechanikában az impulzussal és impulzusnyomatékkal is. Most végigkövetjük az impulzussal kapcsolatos gondolatmenetet, mely nagyban hasonlít az energiával kapcsolatos gon­dolatmenethez. Nézzük tehát a Lagrange-függvényt akkor, amikor nem időbeli, hanem térbeli eltolást vizsgálunk. Most egymásra merőleges x_i y_i és z_i koordinátákat használjunk, és tételezzük föl, hogy az adott mechani­kai rendszer potenciális energiája csak a részecskék koordinátáinak kü­lönbségétől függ:

V = V x_i - x_k , y_i - y_k , z_i -z_k

(Newton III. mozgástörvényének megfelelően a hatás egyenlő az ellen­hatással, azaz a reakcióerővel.) Ebben az esetben a transzformáció a kö­vetkezőképpen írható fel:

x_i = x_i'+a y_i = y_i b z_i = z_i g 12.

ahol a, ß és g állandók, és sem a rendszer potenciális, sem a kinetikus ener­giáját nem változtatják meg, és ismét egy olyan példát kapunk a variációs integrálra, ami bizonyos transzfonnációk esetén invariáns marad (jelen eset­ben a transzformációt a 12. egyenlet dinamikus változóira alkalmazzuk, és a koordináta rendszernek csak a transzlációit vizsgáljuk). Ismét úgy végezzük a transzformációt, hogy az a, ß és g konstansok a t, idő függvényei legyenek, ami három új szabadsági fokot ad a variációs problémának. Ezek a most hozzáadott szabadsági fokok nem jelennek meg a potenciális energiában, azonban a rendszer kinetikus energiája most a következő alakot ölti:

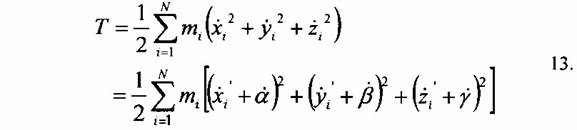
és feltételezve, hogy a, ß és y infinitezimálisan kicsiny, a következő egyenletek adódnak:

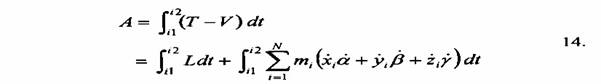
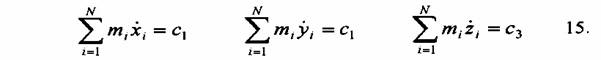Az új a és g hatásváltozókkal a Lagrange-egyenlet alakja a következő lesz:

Ezek az egyenletek a lineáris impulzusmegmaradást írják le, ami jól is­mert a klasszikus mechanikában. (Ha nem is hangsúlyoztuk ki külön, de itt is látható, hogy a levezetés potenciálos, konzervatív erőterekre érvényes.)

Harmadik példaként vizsgáljuk meg a Lagrange-függvényt akkor, ami­kor az a forgásra invariáns. Legyen ekkor a V potenciális energia centrális erők eredménye (melyek szintén konzervatív erőteret eredményeznek), ebben az esetben a V potenciál csak két részecske közti távolságtól függ, azaz a következő mennyiségtől:

Ebben az esetben nemcsak egy konstans transzláció, hanem egy kons­tans rotációforgás is változatlanul hagyja mind a potenciális, mind a kine­tikus energiát, és újra egy Noether-típusú problémához jutunk. A koordi­náták infinitezimálisan kicsiny forgását a következőképpen írhatjuk fel, amennyiben a vektoranalízis összefüggéseit használjuk:

ahol W egy tetszőlegesen kicsiny, infinitezimális vektor. Amennyiben feltételezzük újra, hogy omega a t idő függvénye, a potenciális energia független lesz omegától, de a kinetikus energia a következő formát ölti:

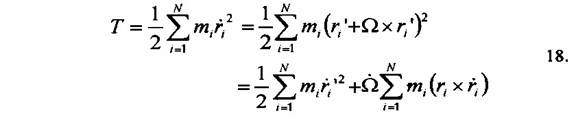Ismét három új szabadsági fokot kapunk azzal, hogy a hatásváltozók­hoz adjuk az W vektort. A Lagrange-egyenletek, melyek az W vektorhoz kapcsolódnak, most a következő összefüggést adják:

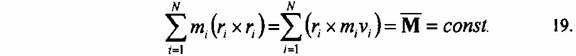
ami fizikailag azt jelenti, hogy a teljes impulzusnyomaték megmarad, ami bármely mechanikus rendszerben igaz, amennyiben centrális erők hatnak. Ez jól alkalmazható például a naprendszerre, és közvetlenül leszármaztat­ható így a Kepler-féle felületsúrolási törvény.

Mivel ez a rövid ismertetés nem terjed ki a több térdimenziós variációs problémákra, ezért nem tudjuk most itt felsorolni a fizika térelméleteinek alkalmazásait a Noether-elv felhasználásával. Legyen elég most csak annyi, hogy ezek a bizonyos elhanyagolható hatásváltozók (azaz olyan pszi dinamikus változók, amelyek a variációsprobléma Lagrange-függvé­nyében nem jelennek meg, pusztán a y x_i, ..., y x_n parciális deriváltjaik jelennek meg. Ezek az Euler-Lagrange-egyenletben a követ­kező alakot öltik:

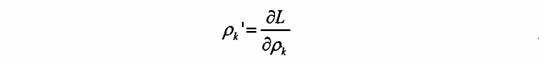ahol a következő jelölést használjuk:

azaz, abban az esetben, ha három tér és egy idő koordinátát használunk, akkor x =x₁ , y=x , z=x , t=x

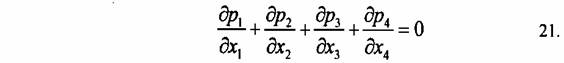
Az anyagi részecskék mechanikájában csak az  x₄ = t van jelen, és a

p = const. azonnal integrálható, és a dp / dt = állandó eredmény­re vezet, ami önmaga is egy megmaradási törvény. Abban az esetben, ha a 21. formájú törvényt használjuk egy mező leírására, a következő konklú­ziókhoz juthatunk. Amennyiben egy háromdimenziós térfogatra terjeszt­jük ki az integrált, és az első három tagot Gauss-transzformációval térfo­gati integrálból átírjuk felületi integrálba. Ha a vektorjelölést használjuk, és a p₁, p₂, p₃ komponenst a p vektor összetevőiként fogjuk fel, akkor ilyen írásmódban a következő vektorformában megadott egyenlethez ju­tunk:

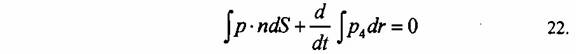
vagy

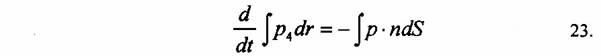
A dg jelöli a térfogatelemet, az n az S határoló felület normálisát jelen­ti, amelynek felületeleme dS. Ezt az egyenletet megint megmaradási tör­vényként foghatjuk fel, ha az òP dt mennyiséget vizsgáljuk, ami lehet a teljes tömeg vagy energia, vagy töltés, vagy momentum az adott helyzettől függően. Ez a mennyiség egy adott térfogatban található, míg a 23. egyenlet jobb oldala a tömeg, energia vagy töltés fluxusaként értelmezhető, ami az S felszínen folyik át. (Ha az integrálást a teljes végtelen térbe kiterjesztjük, akkor a felületi integrál általában eltűnik, és időfüggetlen egyenletekhez jutunk a teljes tömegre, energiára vagy töltésre vonatkozóan.)

Tegyük most fel, hogy egy olyan Lagrange-függvényünk van, amely a y hatásváltozótól függ, de nem függ explicit módon az x₁, x₂, x , x koordinátáktól (a pontmechanika konzervatív rendszerének megfelelően, ahol az L Lagrange-függvény nem függ explicit módon az időtől). Ekkor a következő alakba írhatjuk a hatásintegrált, amely a négy koordináta

x x transzformációjához tartozik, a következő infinitezimális transzformációnak megfelelően:

x_i = x_i' + a_i 25.

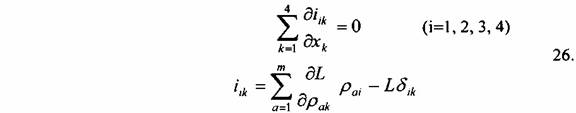Amennyiben az a_i pusztán állandó (transzlációtól független, transzlá­ciósan invariáns), akkor a hatásintegrál formája változatlan marad a határt kivéve, ahol az a_i megjelenik. Azonban, ha olyan alakúra akarjuk hozni a négy a_i értékét, mely függ az x₁, ...,  x függvényektől, mely függvények eltűnnek a határon, így újabb négy szabadságfokot kapunk, amelyek ma­guk nem jelennek meg a Lagrange-függvényben, csak a a a_i x_k parci­ális deriváltjaik. Ennek megfelelően az a_i variációja a következő alakú négy egyenletet fogja adni:

ahol ni a    y y y_m hatásváltozók száma, amíg P_ak jelöli a y_a x_k és a _ik Kronecker-szimbólum. Amennyiben csak egyetlen változó van, és ez az x t, akkor t_ik a t₄₄ mennyiségre redukálódik, ami a rendszer teljes energiája lesz. Így tehát a következő mennyiséget:

ò t₄₄  dt

a következő alakban, a rendszer teljes energiájaként értelmezhetünk, ahol a felületi integrál alakja a következő:

és így energiafluxusként is értelmezhető, mely az S felszínen áthalad. Így az energiamegmaradási törvényhez jutottunk újra. Amennyiben ehhez a törvényhez három további megmaradási törvényt adunk, melyben a következő mennyiségek szerepelnek:

ò t_i4  dt (i = 1, 2, 3)      29.

melyek a lineáris impulzus komponenseiként értelmezhetőek, és az adott mező térfogatelemébe vannak bezárva. Így az energia és impulzus meg­maradása szétválaszthatatlanul összekapcsolódik minden mezőnél, ahol az alapvető Lagrange-függvény nem függ explicit módon a tér- és idő-koordinátáktól, és ahol a t_ik mennyiségek az úgynevezett kanonikus energiamomentum, energia-impulzus tenzor komponenseiként fogható föl. Láthattuk az eddigiekben, hogy a Noether-féle levezetés megadta ugyan az energia, az impulzus és impulzusnyomaték értelmezését mint szimmetriát, de azt is láttuk, hogy ezek csak konzervatív skalárpotenciál­lal leírható esetre érvényesek. Emiatt nem tekinthető teljesen általánosnak az energia- és impulzusmegmaradás, viszont nem vizsgálták meg, hogy nemkonzervatív mezők esetén mi a helyzet.