Képlékenyalakítás alapfogalmai

Képlékenyalakítás alapfogalmai

1 Alakváltozás állapot

Maradó (képlékeny) alakváltozás jellemzésére a valódi, vagy logaritmikus nyúlást használjuk.

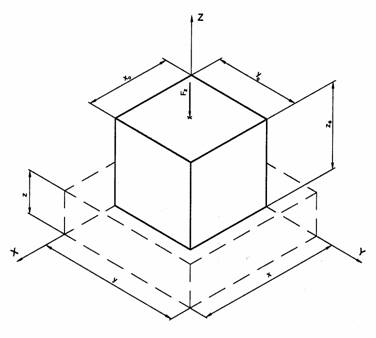
1.1 ábra.

A 1.1 ábrán látható, egységnyi élhosszúságú (x_o = y_o = z_o = 1) kockát F_z erővel, súrlódásmentes körülmények között x, y, z élhosszúságúra alakít 545h77f va, az egyes élek irányában létrejövő valódi nyúlások mérőszámai a

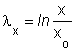
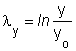
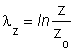
összefüggésekkel határozható meg.

Tételezzük fel, fennáll a λ_x ³ _y ³ _z  reláció, ekkor λ _{x y z} , tehát a főnyúlások koordináta-rendszere megegyezik az x, y, z koordináta-rendszerrel.

Síkalakváltozásról beszélünk, ha valamelyik tengely irányában nem jön létre méretváltozás, tehát a valódi nyúlás értéke zérus.

Az alakítás előtti és utáni térfogat állandóságát a

képlet fejezi ki.

A térfogatállandóságból következik a

illetve a

összefüggés.

Az alakváltozás során elszenvedett összehasonlító alakváltozás értéke a főnyúlások ismeretében a

vagy a

képlettel számítható. Az utóbbi két összefüggés azonosság, ami a térfogatállandóságból kapott

összefüggés felhasználásával bizonyítható.

1 példa

Egy x_o = 40 mm, y_o =  40 mm és z_o = 60mm kiinduló méretű hasábot zömítünk z irányban. A zömítés utáni méretei: x = 55 mm, z = 30 mm.

Homogén alakváltozásállapotot feltételezve, határozza meg az x, y és z tengely irányú valódi nyúlást és az alakváltozott hasáb pontjaiban az összehasonlító alakváltozást.

1 példa megoldása

Kiinduló adatok:

A hasáb kiinduló méretei: x_o = 40 mm, y_o = 40 mm, z_o = 60 mm

A hasáb zömítés utáni méretei: x = 48 mm, z = 30 mm

A térfogatállandóságot felhasználva:

Amelyből a z = 30 mm-re zömített hasáb y irányú mérete:

y = 66,67 mm

A valódi nyúlások az x, y és z tengely irányában:

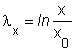
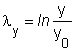
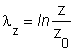
_x λ_y 0,511 λ_z

A főnyúlásokra érvényes reláció alapján írható:

                  

Az összehasonlító alakváltozás a hasáb pontjaiban:

2 Alakváltozás-sebesség állapot

Az x, y és z tengely irányában létrejövő alakváltozás-sebességek, a valódi nyúlások időegységre vetített értékeinek tekinthetők, azaz:

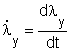
összefüggésekkel számítható.

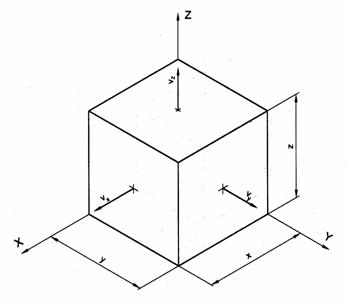
2.2 ábra

Ismerve a 2.2 ábrán látható alakváltozó hasáb x, y és z normálisú lapjainak v_x, v_y és v_z elmozdulássebességeit (amelyekről most tételezzük fel, hogy állandók), akkor az előbbi összefüggések felhasználásával a koordinátarendszer tengelyeinek irányában a pillanatnyi deformált állapothoz (x, y, z élhosszúsághoz) tartozó alakváltozás-sebességek a

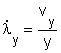
összefüggésekkel határozhatók meg.

Ha teljesül a reláció, akkor igaz a

összefüggés-csoport, következésképpen a főnyúlások koordináta-rendszere azonos az x, y, z koordináta-rendszerrel.

A térfogatállandóságból következik a

illetve a

összefüggés.

Az összehasonlító alakváltozás-sebesség a főalakváltozás-sebességek ismeretében a

vagy a

összefüggéssel határozható meg.

A 2.1 táblázat tájékoztató értékeket közöl néhány képlékenyalakító technológia összehasonlító alakváltozás (λ_ö) és összehasonlító alakváltozás-sebesség tartományáról ().

2.1 táblázat

2 példa

Egy x_o = 40 mm, y_o =  40 mm és z_o = 60mm kiinduló méretű hasábot zömítünk z irányban, v_z = -0,5 mm/s állandó nyomószán-sebességgel, úgy hogy az y tengely irányában az alakváltozást a szerszám megfelelő kialakításával megakadályozzuk.

Homogén alakváltozás-sebesség állapotot feltételezve, határozza meg a hasáb pontjaiban az x, y és z tengely irányú alakváltozás-sebességeket és az összehasonlító alakváltozás-sebességet, a hasáb z = 30 mm-es zömítési magasságánál.

2 példa megoldása

Kiinduló adatok:

A hasáb alakítás előtti méretei: x_o = 40 mm, y_o = 40 mm, z_o = 60 mm

A "z" irányú szerszámsebesség: v_z = -0,5 mm/s

A hasáb adott z=30mm zömítési magasságához tartozó további méretei:   y = y_o

A térfogatállandóságot felhasználva:

és figyelembe véve: y = y_o

A hasáb "x" irányú mérete: x = 80 mm

A "z" irányú alakváltozás-sebesség:

A kontinuitási törvényből következik:  

Mivel: v_y ezért

így:

A főnyúlássebességekre érvényes reláció miatt írható:

Az összehasonlító alakváltozás-sebesség:

3 Képlékenységi feltétel

Tételezzük fel, hogy a 1 ábrán látható kocka zömítését F_z erővel úgy végezzük, hogy közben az x és y normálisú lapokon F_x illetve F_y erőket működtetünk.

Kérdés: a fenti erők milyen értéke mellett indul meg a képlékeny alakváltozás, majd ezt követően hogyan változzon az F_z zömítőerő a zömítési út függvényében, hogy a zömítési folyamat fenntartható legyen?

A kocka pontjaiban az x, y és z tengelyek irányában ébredő feszültségek az alakítás kezdeti pillanatában a

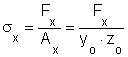
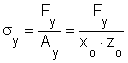
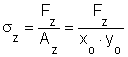
összefüggésekkel határozhatók meg.

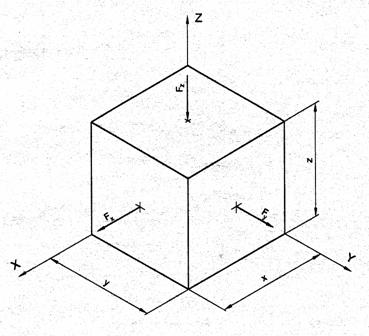
1. ábra

A képlékeny állapot létrejöttének, illetve folyamatos fenntartásának feltétele, hogy a feszültségekből számítható összehasonlító feszültség (s ) érje el az anyag pillanatnyi összehasonlító alakváltozásához tartozó alakítási szilárdság (k_f) értéket, azaz:

Adott anyagminőség alakítási szilárdsága (k_f) az alakváltozás során nem állandó, az állapothatározó paraméterek függvénye.

Ebből következik, hogy az előbbi összefüggés bal oldalán szereplő összehasonlító feszültség értékének úgy kell változni, hogy az egyenlőség az alakítási folyamat során fennmaradjon. A gyakolatban ez azt jelenti, hogy a 1 ábrán látható alakítási modellt hidegalakítás körülményei között zömítve a növekvő alakváltozás (csökkenő "z" irányú méret), növekvő alakítóerővel tartható fenn.

Tételezzük fel, hogy fennáll a s_x ³ s_y ³ s_z reláció. Ekkor a főfeszültségek s s_x s s_y s s_z és a főfeszültségek koordináta-rendszere azonos az x, y, z koordináta-rendszerrel.

A főfeszültségekkel az összehasonlító feszültség értéke Tresca elmélete szerint a

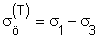
Huber - Mises - Hencky elmélete szerint

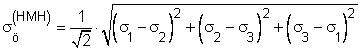
összefüggéssekkel számítható.

A két elmélet bizonyos feszültségállapotoknál azonosan, másoknál eltérően itéli meg a képlékeny állapot létrejöttének, illetve folyamatos fenntartásának feltételét. Legnagyobb az eltérés a

összefüggéssel jellemzett feszültségállapot esetén (kb. 15%).

3 példa

Külső erőkkel terhelt acél próbatest valamely pontjában s  = 400 [N/mm s  = 300 [N/mm s  = -600 [N/mm ] fesültségállapot ébred. A próbatest anyaga homogén és izotróp, ezért valamennyi pontjában az alakítási szilárdság k_f = 1000 [N/mm

Vizsgálja meg a Tresca és a Huber-Mises-Hencky képlékenységi feltétellel, hogy rugalmas vagy képlékeny állapotban van a vizsgált pont és annak szűk környezete?

3 példa megoldása

Kiinduló adatok:

A vizsgált pontban a főfeszültségek értékei:

s  = 400 [N/mm s  = 300 [N/mm s  = -600 [N/mm

Alakítási szilárdság a vizsgált pontban: k_f = 1000 [N/mm

Összehasonlító feszültség Tresca szerint: [N/mm

Összehasonlító feszültség Huber-Mises-Hencky szerint:

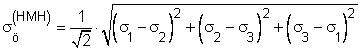
[N/mm

A képlékeny állapot létrejöttének a feltétele, hogy az összehasonlító feszültség érje el az adott pont alakítási szilárdságát, azaz:

, illetve

A számított értékek alapján megállapítható, hogy a Tresca hipotézis szerint a vizsgált pont képlékeny állapotban, a Huber-Mises-Hencky szerint rugalmas állapotban van.

4 Anyagtörvény képlékeny állapotban

Ha a képlékeny állapotban létrejött valódi nyúlás értékek mellett (l_x l_y l_z), a képlékeny alakváltozás megindulását mindig megelőző rugalmas alakváltozások elhanyagolhatóak (mert egy-két nagyságrenddel kisebbek a képlékeny alakváltozás során létrejött alakváltozásokhoz képest), akkor a feszültségek és az alakváltozások kapcsolatának jellemzésére jól használhatók a Mises által javasolt

egyenletek.

ahol: D - a képlékenységi modulus.

Az alakítási folyamat során D értéke nem állandó, hanem az összehasonlító alakváltozás függvénye a

elvi összefüggésnek megfelelően (ha állandó összehasonlító alakváltozás-sebességgel és állandó hőmérsékleten megy végbe az alakváltozás).

A Mises-egyenletek és a folyási feltétel felhasználásával levezethető a

összefüggés, amelynek elvi diagramja a 4.1 ábrán látható, s tulajdonképpen az anyagtörvény grafikus formája.

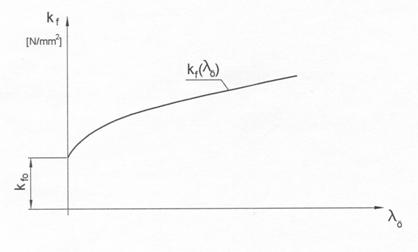
4.1 ábra

A k_f - λ_ö függvényt az adott anyagminőség folyásgörbéjének nevezzük.

Az origóból a folyásgörbe egy tetszőleges pontjához egyenest húzva, az egyenes vizszintes tengellyel bezárt hajlásszögének tangense:

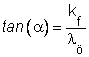
Ez nem más mint az adott folyásgörbe ponthoz tartozó képlékenységi modulus (lásd: a Mises egyenletekből felírt összefüggést).

A képlékenységi modulus értéke a folyásgörbe pontjaiban más és más, ezért a fent felírt Mises egyenletek csak az adott ponthoz tartozó feszültség- és alakváltozásállapot közötti kapcsolatot jellemzik.

4 példa:

Síkbeli feszültségállapottal (_a > 0, _b > 0, _c = 0) terhelt lemez "A" pontjában -az alakváltozási állapot mérésére- a lemez felületére d_o = 5 [mm] átmérőjű kört viszünk fel.

Az alakítás után ellipszissé torzult kör nagy- és kistengelyének méretei:

a = 7,3 [mm], b = 6.2 [mm].

Határozza meg:

a./ a l összehasonlító alakváltozást az "A" pont környezetében

b./ az összehasonlító alakváltozás l_a l_b komponenseit létrehozó _a, _b feszültségeket, ha a lemez anyagának folyásgörbe paraméterei:
                                 c = 147 [N/mm²], n = 0,2.

4 példa megoldása

Kiinduló adatok:

Az etalon kör átmérője: d_o = 5 [mm]

Az alakváltozás során ellipszissé torzult etalon kör nagy- és kistengelyének mérete:     a = 7,3 [mm], b = 6.2 [mm].

A lemez anyagának folyásgörbe paraméterei:

keményedési együttható: c = 147 [N/mm²], keményedési kitevő: n = 0,2

Valódi nyúlás a nagytengely irányában: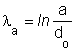

Valódi nyúlás a kistengely irányában: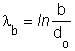

A lemez síkjára merőleges valódi nyúlás a összefüggés felhasználásával számítható:

Az összehasonlító alakváltozás a három egymásra merőleges valódi nyúlással:

Az alakítási szilárdság a vizsgált pontban: [N/mm²]

A képlékenységi modulusz: 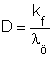[N/mm²]

A Mises-egyenletek az a, b és c irányban az alábbi alakúak:

Figyelembe véve, hogy a lemez csak a síkjában terhelt, azaz a lemez síkjára merőleges feszültség zérus (), ezért a fenti egyenletek az alábbi alakra egyszerűsödnek:

Mivel bármelyik két egyenlet meghatározza a harmadikat, ezért nem függetlenek egymástól.

Például az első két összefüggést felhasználva a _a, _b feszültségek kifejezhetők.

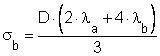
[N/mm²] [N/mm²]

5 Folyásgörbe, folyási felület

Adott anyagminőség alakítási szilárdságát a

háromváltozós függvény írja le.

A három változó közül (az összehasonlító alakváltozás-sebességet állandó értéken tartva) és az alakítási szilárdságot a másik két változó függvényében ábrázolva, olyan kétváltozós függvényt kapunk, amelynek összetartozó értékei egy felületen helyezkednek, amelyet a 5.1 elvi ábra szemléltet. Az így kapott felületet folyási felületnek nevezzük.

Szobahőmérsékleten, kis összehasonlító alakváltozás-sebességgel () végezve az alakítást, az alakítási szilárdság jó közelítéssel csak az összehasonlító alakváltozás függvényeként kezelhető, mivel a másik két paraméter befolyásoló hatása ezen a hőmérsékleten nem jelentős.

A folyásgörbe adott összehasonlító alakváltozássebesség értékhez tartozó folyási felület,
T = áll. hőmérsékleten vett metszete, tehát a

függvénykapcsolatot jelenti, vagyis az alakítási szilárdság változását az összehasonlító alakváltozás függvényében, miközben a másik két paramétere állandó értékű.

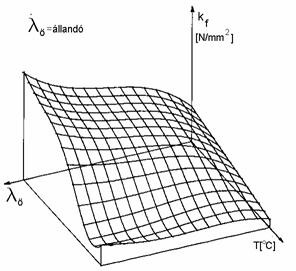
5.1 ábra

A 5.2 ábra néhány anyag T = 20 C alakítási hőmérsékleten, 0,1 [1/s] összehasonlító alakváltozás-sebességgel felvett folyásgörbéjét és a deformáció során a térfogategységben elnyelt ideális alakváltozási munkát szemlélteti.

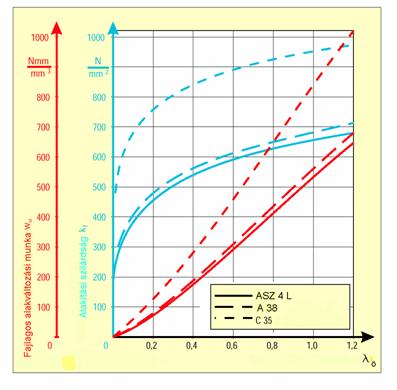
5.2 ábra

5.1 Folyásgörbe meghatározás módszerei

A képlékenyalakító technológia erő- és munkaszükségletének meghatározásához ismernünk kell az alakított fém folyásgörbéjét, a technológia által meghatározott összehasonító alakváltozás-sebességen és alakítási hőmérsékleten.

Az alakítandó anyag folyásgörbéje a fenti paraméterek ismert értékei mellett méréssel és a kapott mérési adatok felhasználásával végzett számítással határozható meg.

A folyásgörbe meghatározása méréstechnikailag nem egyszerű feladat, mert a mérés során nehéz biztosítani, hogy az alakváltozás -az alakítási szilárdság definíciójának megfelelően- egytengelyű feszültségállapotban menjen végbe, továbbá a próbatest hőmérséklete és összehasonlító alakváltozás-sebessége mérés közben állandó értékű legyen.

A kifejlesztett módszerek más és más megközelítésben oldják meg a fenti feltételek teljesülését.

A fontosabb mérési módszerek:

Hengeres próbatest zömítővizsgálatával végzett folyásgörbe meghatározás,

Hengeres próbatestek zömítővizsgálatával végzett folyásgörbe meghatározás (extrapolációs módszer),

Lapos próbatest zömítővizsgálatával végzett folyásgörbe meghatározás (Watts - Ford módszer),

Folyásgörbe meghatározás hengeres próbatest zömítővizsgálatával

Az egytengelyű feszültségállapot jó közelítéssel megvalósítható a d_o kiinduló átmérővel és h_o kezdő magassággal rendelkező hengeres próbatest zömítése során, ha gondoskodunk arról, hogy az alakváltozó próbatest véglapjai és a szerszámfelületek (nyomóbetétek) között a súrlódás elhanyagolhatóan kis értékű legyen. Ez elérhető az érintkező felületek előzetes polírozásával és megfelelő kenéssel.

A h magasságra zömített d átmérőjű próbatest véglapjain az átlagnyomás a

összefüggéssel határozható meg (lásd: [2]).

Ha a súrlódás elhanyagolhatóan kis értékű (m  0), akkor az átlagnyomás az alakítási szilárdsággal vehető azonosnak, amelyet a

összefüggés szemléltet.

A

összefüggéssel az átlagnyomás meghatározható a h magassághoz tartozó F zömítőerő és a nyomott "A" felület hányadosaként, ahol a h magassághoz tartozó keresztmetszet a térfogatállandóságból felírható

képlettel számítható.

Tehát a zömítési tartományban az összetartozó F és h értékek felhasználásával az alakítási szilárdság a

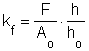
az összehasonlító alakváltozás pedig

összefüggésekkel határozható meg.

Mérés gyakorlati kivitelezése

A mérés gyakorlati kivitelezése a 5.2.1 ábrán látható elvi vázlat szerint végezhető. Az erőmérés a nyomóbetét és a nyomószán közé épített erőmérő cellával, az útmérés pedig az útadóval történik. A mérőegységek analóg jelét az X - Y író megfelelő bemeneteire kapcsolva, a zömítés erő - út diagramja regisztrálható.

A regisztrátumból -az erő- és útlépték ismeretében- az összetartozó F - Dh, illetve a

összefüggés felhasználásával az F - h adatpárok előállíthatók.

A zomites.ppt Power Point file diasorozata "Diashow" üzemmódban lejátszva, a GO3 MSZ17789 anyagminőségű, h_o = 20 mm kiinduló magasságú és d_o = Æ10 mm kiinduló átmérőjű hengeres próbatest súrlódásmentes körülmények között (m = 0), szobahőmérsékleten, h = 5 mm végső magasságig végzett zömítési szimulációját szemlélteti. Jól megfigyelhető a kezdeti rácsháló a súrlódásmentes viszonyok miatt nem torzul, tehát az alakváltozás egytengelyű feszültségállapotban megy végbe. A zömítés során az alakváltozási munka hővé alakul, s a darab pontjainak

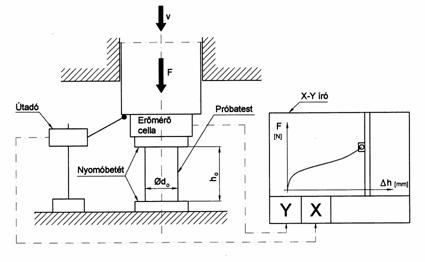
5.2.1 ábra

hőmérsékletét növeli. A színskála a darab hőmérséklet eloszlásáról tájékoztat. Az ábrán a zömítés erő-út diagramjának egy részlete is megfigyelhető.

Függvényillesztés

Az összetartozó k_f - λ_ö értékeket diagramban ábrázolva a 5.2.2 ábrán látható pontsort kapjuk.

5.2.2. ábra.

A számított pontsorra célszerű egy alkalmasan megválasztott függvényt illeszteni. A gyakorlatban gyakran alkalmazzák a folyásgörbe leírására a

alakú egyszerű hatványfüggvényt, azon hibája ellenére, hogy a kis alakváltozások tartományában (λ_ö = 0...0,3) pontatlanul jellemzi a k_f - λ_ö kapcsolatot, viszont matematikailag jól kezelhető (könnyen deriválható, integrálható, stb.).

5.2.3 ábra

A függvény paraméterei a "c" keményedési együttható és az "n" keményedési kitevő. Az utóbbi értéke 0 £ n £ 1 tartományban van. Bizonyítható (lásd: [1]), hogy a keményedési együttható értéke az egységnyi összehasonlító alakváltozáshoz (λ  = 1) tartozó alakítási szilárdság értékével azonos, továbbá az "n" keményedési kitevő értéke nem más, mint az adott anyag szakítóvizsgálata során, az egyenletes nyúlás felső határához tartozó összehasonlító alakváltozás.

A teljes tartományban hibátlanul jellemzi a folyásgörbét a

alakú négyparaméteres folyásgörbe egyenlet, amely a kis alakváltozások tartományában is jól illeszkedik a mért értékekre.

A c és n, illetve az a, b, c és d paraméterek értékeinek meghatározását a legkisebb négyzetek módszerével végezzük, hogy a keresett függvény a legkisebb hibával illeszkedjék a mért pontsorra.

A 5.2.3 ábra az illesztett egyszerű hatványfüggvény diagramját szemlélteti, feltüntetve a mért pontsor diszkrét értékeit is.

5.2 példa

C25 MSZ61 anyagminőségű, hengeres próbatest zömítése során felvett erő - út diagramból az alábbi összetartozó értékpárokat ( próbatest magasságcsökkenése, zömítőerő) határoztuk meg:

A próbatest kiinduló adatai:    átméröje: do = 20,35 mm,
magassága: ho = 9,95 mm

a./ Határozza meg a folyásgörbe fenti mért adatpárokhoz tartozó pontjait

b./ A folyásgörbe pontokra -a legkisebb négyzetek módszerével- határozza meg a alakú folyásgörbe egyenlet "c" és "n" paramétereit.

5.2 példa megoldása

Az összetartozó összehasonlító alakváltozás és alakítási szilárdság értékek az alábbi összefüggésekkel számíthatók:

                                

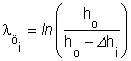
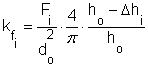
A fenti összefüggésekkel számított értékek:

A legkisebb négyzetek módszerének felhasználásával az "n" keményedési kitevőre és a "c" keményedési együtthatóra az alábbi két összefüggés vezethető le:

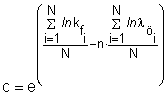
ahol: N - a mért pontok száma, jelen példában: N = 10

A fenti összefüggésekkel számított "n" és "c" értékek:

n =0,218 c = 754,79 [N/mm

A folyásgörbe számított pontsorát és a meghatározott paraméterekkel megrajzolt függvényt szemlélteti a 5.2.4 ábra:

5.2.4 ábra

6 Anyagmodellek. Közepes alakítási szilárdság

Fémes anyag képlékeny alakváltozása során, az alakváltozási állapot és feszültségi állapot közötti nemlineáris kapcsolatot az anyag folyásgörbéje jellemzi.

A nemlineáris viselkedés, a képlékenyalakító technológia modelljének matematikai megfogalmazásánál (pl.: alakítás erő-, munka- és teljesítményszükséglete) legtöbbször nem teszi lehetővé a keresett ismeretlen zárt alakban történő kifejezését. Ekkor az ismeretlen meghatározása numerikus módszer alkalmazásával történhet.

A zárt alakú megoldhatóság érdekében a valós anyagmodellt idealizált anyagmodellel helyettesítik. Ez a megoldás pontatlanságát növeli, de általában még kielégíti a gyakorlat támasztotta pontossági követelményeket.

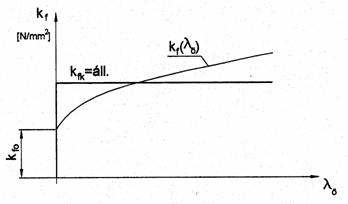
6.1 ábra

Ideálisan merev, tökéletesen képlékeny anyagmodell

Ideálisan merev, tökéletesen képlékeny anyagmodellt szemléltet a 6.1 ábra. Az ilyen viselkedésű anyag rugalmassági modulusza végtelen (E = ¥), tehát nincs rugalmas alakváltozása a képlékeny alakváltozás megindulása előtt. Amint az összehasonlító feszültség elérte a folyáshatárt, annak értéke változatlan marad (k_f = áll.) a képlékeny alakváltozás teljes tartományában (nincs felkeményedés).

Például a 6.2 ábrán látható kúpos csatornában végzett alakítások modellezése során feltételezik, hogy az alakváltozási zónában (a csonkakúp alakú térfogatrészben) az alakítási szilárdság helytől függetlenül állandó értékű. A csatorna be- és kilépő keresztmetszete közötti tartományban (k_fk =  áll.) közepes alakítási szilárdsággal modellezzük az alakított anyagot, vagyis ideálisan merev, tökéletesen képlékeny anyagmodellt alkalmazunk.

A közepes alakítási szilárdság a képlékeny zóna legkisebb és legnagyobb összehasonlító alakváltozást szenvedett pontjaihoz (a be- és kilépő keresztmetszet pontjai) tartozó összehasonlító alakváltozás tartomány integrálközép értékeként határozható meg a

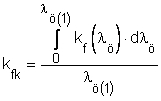
összefüggéssel, ahol a kúpos csatorna kilépő keresztmetszetében az összehasonlító alakváltozás

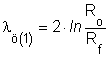
képlettel számítható.

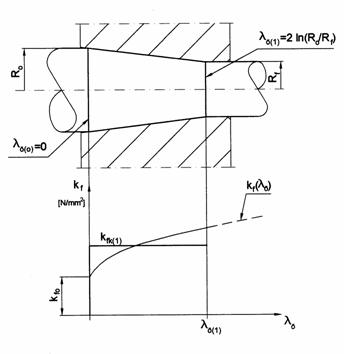
6.2 ábra

A közepes alakítási szilárdság kevésbé pontos értékét megkaphatjuk a képlékeny zóna legkisebb és legnagyobb alakítási szilárdságú pontjainak számtani középértékeként. A kúpos csatorna példát felhasználva, tételezzük fel: a belépő keresztmetszethez k_fo alakítási szilárdsággal érkezik az anyag (nincs előalakítás), a kilépő keresztmetszetben (a felkeményedés miatt) az alakítási szilárdság

képlettel számítható. A számtani középpel számított közepes alakítási szilárdságot a

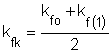
összefüggés adja.

Meg kell jegyezni, a számtani középpel akkor határozható meg elfogadható pontossággal a közepes alakítási szilárdság, ha a két szomszédos k_f érték a folyásgörbe közel lineáris szakaszán van, vagy a kezdeti szakaszon akkor ha közel helyezkednek el egymáshoz képest.

Ideálisan merev, lineárisan keményedő anyagmodell

Ideálisan merev, lineárisan keményedő anyagmodell elvi vázlatát szemlélteti a 6.3 ábra.

A nemlineáris viselkedést a valós folyásgörbe pontokra illesztett egyenessel amely átmegy a k_fo ponton linearizálja.

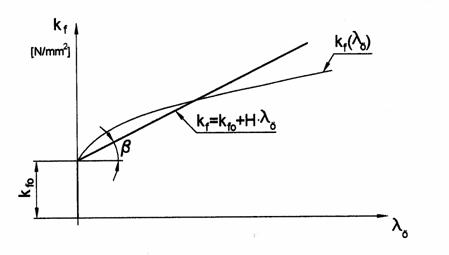
6.3 ábra

Az idealizált anyag folyásgörbe egyenlete:

ahol

az illesztett egyenes vizszintessel bezárt b hajlásszögének iránytangense.

6 példa

C10 minőségű, d_o= 5 mm átmérőjű huzalt, félkúpszögű húzógyűrűben d_f = 4.2 mm átmérőjűre húzunk, szobahőmérsékleten. A húzógyűrűbe befutó anyag teljesen kilágyított állapotban van, alakítási szilárdsága k_fo = 186,4 N/mm².

A húzott anyag folyásgörbe paraméterei:

keményedési együttható: c = 683,5 N/mm²,

keményedési kitevő:  n = 0,235

A Coulomb-féle súrlódási tényező értéke a húzás során: m

Határozza meg:

a./ a húzógyűrű kilépő keresztmetszetében a huzal alakítási szilárdságát,

b./ a be- és kilépő keresztmetszet között lévő anyag közepes alakítási szilárdságát,

c./ a kihúzás fajlagos és teljes erőszükségletét.

6 példa megoldása

Kiinduló adatok:

Huzal átmérő a húzás előtt: d_o= 5 mm , húzás után: d_f = 4.2 mm

Húzógyűrű félkúpszöge fokban: radiánban: p

Az alakított anyag egyszerű hatványfüggvénnyel jellemzett folyásgörbéjének paraméterei: c = 683,5 N/mm², n = 0,235

Az alakítatlan anyag alakítási szilárdsága: k_fo = 186,4 N/mm².

Súrlódási tényező a húzógyűrű kúpos palástján: m = 0,1

A kilépő keresztmetszetben a λ_r radiális, a λ_t tangenciális írányú valódi nyúlás:

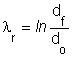a hengerszimmetria miatt:

Az axiális irányú valódi nyúlás a térfogatállandóságból levezetett

összefüggés felhasználásával határozható meg:  

Az összehasonlító alakváltozás a kilépő keresztmetszetben:

Alakítási szilárdság a kilépő keresztmetszetben:

                    N/mm²

Az eddigi eredmények birtokában a húzógyűrű ki- és belépő keresztmetszete közötti anyag (képlékeny zóna) közepes alakítási szilárdsága számtani középpel egyszerűen meghatározható, bár pontossága kifogásolható, mert ebben a tartományban a folyásgörbe nem tekinhető közel lineárisnak.

N/mm²

Az integrálközéppel történő meghatározás elve, hogy téglalap területe egyezzen meg a tartományban vett folyásgörbe alatti területtel.

Tehát: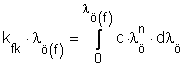                             

A jobboldali integrált meghatározva: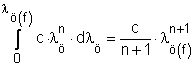

majd helyettesítve az előbbi összefüggésbe, rendezés után írható:

N/mm²

Mint várható volt jelentős az eltérés a két módszerrel számított érték között.

A fajlagos húzóerőt a Siebel összefüggéssel határozhatjuk meg. E szerint a húzási folyamat folyamatos fenntartása érdekében a kilépő keresztmetszetben működtetendő húzófeszültség :

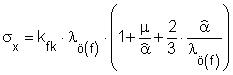
összefüggéssel határozható meg.

Az integrálközéppel számított közepes alakítási szilárdsággal a húzás fajlagos erőszükséglete: N/mm²

Ez kielégíti a húzás feltételét: , így a húzás biztonságosan elvégezhető.

A teljes húzóerő a fajlagos húzóerő és a kilépő keresztmetszet szorzataként határozható meg.

A húzógyűrűből kilépő huzal keresztmetszete:    mm

A húzóerő:         

N

7 Alakítás munkaszükséglete

A technológia által meghatározott úton, megfelelő nagyságú alakítóerő működtetésével valósítható meg a kezdeti alak megváltoztatása a kívánt geometriára.. A legtöbb képlékenyalakító technológiánál az alakítóerő értéke nem állandó, az alakítási út függvényében változik.

Tehát az alakítás munkaszükséglete nem más mint az alakítási út során rendszerint változó alakítóerő munkája.

Ideális körülmények között (súrlódás elhanyagolhatóan kicsiny, azaz m  0) az alakítóerő által végzett munka döntő részben a képlékeny alakváltozás munkaszükségletét fedezi és a képlékeny zónában nyelődik el.

A meghatározásának elvét a hengeres darab axiális irányú nyújtásával szemléltetjük.

Térfogategységben elnyelt elemi alakítási munka

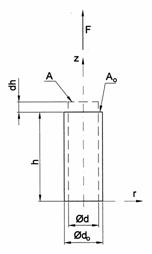
7.1 ábra

Hengeres darab axiális irányú nyújtásának elvi vázlatát a 7.1 ábra szemlélteti.

A d_o átmérőjű és h_o hosszúságú hengeres darabot F erővel axiális irányban dh értékkel megnyújtva a végzett elemi munka a

összefüggéssel határozható meg.

A megnyújtás következtében a kezdeti A_o keresztmetszet A-ra csökkent, miközben a hossza h_o-ról h-ra nőtt.

Az előbbi egyenlet mindkét oldalát az alakváltozásban résztvevő V térfogattal elosztva -amely a

összefüggéssel számítható- kapjuk a térfogategységben elnyelt elemi munkát:

A folyási függvényből következik a

formula.

Hengeres darab axiális irányú nyújtásánál írható a

valamint a

összefüggés.

A fentiek figyelembevételével a térfogategységben elnyelt elemi munka a következő összefüggéssel is kifejezhető:

ahol az alakítási szilárdság maga is az összehasonlító alakváltozás függvénye, tehát:

Térfogategységben elnyelt alakítási munka és a folyásgörbe alatti terület kapcsolata

Az axiális irányú nyújtás során a kezdeti h_o hosszt h₁-re növelve, az alakváltozás során a térfogategységben elnyelt munka az elemi munkára felírt összefüggés felhasználásával határozható meg a

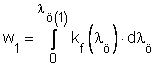
összefüggéssel, ahol:

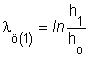
A folyásgörbe jellemzésére, a

alakú, egyszerű hatványfüggvényt használva, kapjuk a

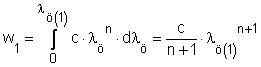
térfogategységben elnyelt alakváltozási munkát.

Teljes térfogatban elnyelt alakítási munka

Homogén alakváltozási állapot esetén (a képlékeny zóna valamennyi pontjában az alakváltozási állapot, ennek következtében az összehasonlító alakváltozás azonos értékű (lásd: hengeres rúd nyújtása). Ekkor a teljes térfogatban elnyelt alakváltozási munka a térfogategységben elnyelt muka és a képlékeny zóna térfogatának szorzataként számítható a

összefüggéssel.

Ha a képlékeny zóna pontjaiban az alakváltozási állapot a hely függvényében más és más értékű (inhomogén alakváltozási állapot), akkor a teljes térfogatban elnyelt alakítási munka a térfogategységben elnyelt munka képlékeny zóna térfogatára vett integráljával állítható elő.

Például Descartes-féle derékszögű koordinátarendszerben a

összefüggést írhatjuk fel, ahol dV az adott koordinátarendszerben felírható térfogatelem.

Henger- illetve gömbkoordináta rendszerben

7 példa

A 6 példa adataival adott huzalhúzásnál határozza meg a húzógyűrűben a d_o és d_f átmérők közötti tartományban lévő anyagrészben elnyelt ideális fajlagos és teljes alakváltozási munkát.

7 példa megoldása

Kiinduló adatok:

Huzal átmérő a húzás előtt: d_o= 5 mm , húzás után: d_f = 4.2 mm

Húzógyűrű félkúpszöge fokban: radiánban: p

Az alakított anyag egyszerű hatványfüggvénnyel jellemzett folyásgörbéjének paraméterei: c = 683,5 N/mm², n = 0,235

Az alakítatlan anyag alakítási szilárdsága: k_fo = 186,4 N/mm².

A térfogategységben elnyelt ideális alakváltozási munka a tartományban vett folyásgörbe alatti területtel arányos.

A 6 példában integrálközéppel meghatározott közepes alakítási szilárdság felhasználásával:        N/mm²

A következő összefüggéssel számítható (a téglalap területe a folyásgörbe alatti területtel azonos):

                J/mm

A csonkakúp térfogata: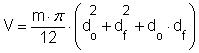

ahol: m- a csonkakúp magassága, jelen példában az d_o és d_f átmérőjű körökkel jellemezhető be- és kilépő keresztmetszetek közötti távolság, amely a félkúpszög ismeretében:

mm

összefüggéssel számítható.

A térfogatot meghatározva: mm

A térfogatban elnyelt ideális alakváltozási munka: J

8 Súrlódás szerepe a képlékenyalakítási folyamatokban

A képlékenyalakító technológiáknál fellépő súrlódási viszonyok jelentősen eltérnek a gépek üzemtanában megismert súrlódási körülményektől. Például a csúszócsapágyak, csúszó vezetékek esetében a kapcsolódó alkatrészek (tengelycsap és csapágypersely) a terhelés hatására rugalmas alakváltozást szenvednek, mert az érintkező felületeken fellépő nyomás ritkán haladja meg a 15 - 20 MPa-t.

Ezzel szemben a képlékenyalakító műveletekben a szerszám rugalmas, a vele érintkező munkadarab képlékeny állapotban van. A felületi nyomás a munkadarab és a szerszám között elérheti az 1000 - 2000 MPa-t is.

Eltérő nagyságrendű a csúszó felületek között létrejövő relatív elmozdulás mértéke és sebessége.

Ezért járulékos problémák keletkeznek a normál súrlódás jelenségeihez képest:

az érintkező felületek között fellépő rendkívül nagy felületi nyomások,

a képlékenyen alakváltozó munkadarab felületkialakulása és

a szerszám és a munkadarab között kialakuló hideghegedések miatt.

8.1 Súrlódás mérőszámai

A képlékenyalakító technológiák tervezésekor, az alakított darab és a szerszám között fellépő súrlódási viszonyok ismerete a technológus számára alapvetően fontos mert:

befolyásolja a képlékeny zóna feszültségi és alakváltozási állapotát,

növeli az alakítóerőt, az alakítás munka- és teljesítményszükségletét,

döntő hatással van a szerszámkopás mértékére, ebből következően a gyártmány alak- és méretpontosságára,

befolyásolja a termék felületi minőségét.

A gyakorlatban a súrlódás nagyságának jellemzése többnyire a Coulomb-féle súrlódási tényezővel, vagy a Kudo-féle súrlódási mérőszámmal történik.

A súrlódást leíró mérőszám nagysága függ:

az alakított darab és az alakító szerszám érintkező felületeinek érdességétől,

az érintkező felületek között lévő kenőanyag tulajdonságaitól,

az alakítási hőmérséklettől (az érintkező felületek hőmérsékletétől),

az érintkező felületek relatív sebességkülönbségétől,

az érintkezési nyomástól.

Coulomb-féle súrlódási tényező

Ha sík felülettel "A" felületen érintkező csúszó hasábot F_n erő szorítja a sík felülethez a 8.1.1 ábra szerint, a súrlódási tényező az F_s súrlódó- és az F_n összeszorítóerő hányadosaként határozható meg a

összefüggéssel.

Az erőket a súrlódó felületre vonatkoztatva, a m súrlódási tényező értéke a felületen ébredő t_s súrlódó feszültség és a s_n normálfeszültség hányadosával is kifejezhető a

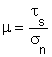
képlettel.

Ha a felületen ébredő normálfeszültség eléri a súrlódó darab anyagának alakítási szilárdságát (s_n   k_f), akkor a két felület között ébredő súrlódó feszültség eléri a képlékeny állapotba került darab anyagának nyírófolyáshatárát (t_s t_f). Ismerve az alakítási szilárdság és a nyírófolyáshatár közötti a

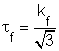
képlet szerinti kapcsolatot, a Culomb-féle súrlódási tényező maximális értéke a

értékű.

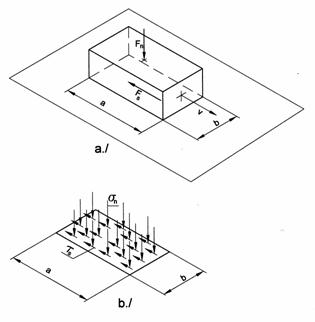
8.1.1 ábra

A Coulomb-féle súrlódási tényező tehát a

tartományban változhat, ahol:

m = 0 súrlódás mentes állapotot,

m = 0,577 tapadásos súrlódást jellemez.

Kudo-féle súrlódási szám

A Kudó-féle értelmezés szerint a súrlódási feszültség a nyírófolyáshatárral arányos, tehát írható a

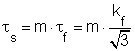
összefüggés.

ahol: 0 £ m £

m = 0 súrlódásmentes állapotot, m = 1 tapadásos súrlódást jellemez.

Súrlódás hatása a zömítés fajlagos alakítóerő-szükségletére

A súrlódás fajlagos alakítóerőre gyakorolt hatását a hengeres darab axiális irányú zömítésére és a kúpos csatornában végzett alakításra levezetett összefüggések jól szemléltetik.

Hengeres darab axiális irányú zömítésének fajlagos erőszükségletét a pillanatnyi zömítési magasság függvényében a

összefüggéssel számítható (lásd: [2]), ahol:

k_f - a pillantnyi zömítési magassághoz tartozó alakítási szilárdság,

m - Coulomb-féle súrlódási tényező értéke a nyomólapok és az alakított darab között,

h - a pillanatnyi zömítési magasság,

d - a pillantnyi zömítési magassághoz tartozó átmérő.

d_o = 10 mm kiinduló átmérőjű, h_o = 20 mm kiinduló magasságú Al99,5 anyagminőségű, hengeres próbatest zömítésének m m m = 0,35 és m = 0,45-ös súrlódási tényezővel számított erő - út diagramját szemlélteti a 8.1.2 ábra.

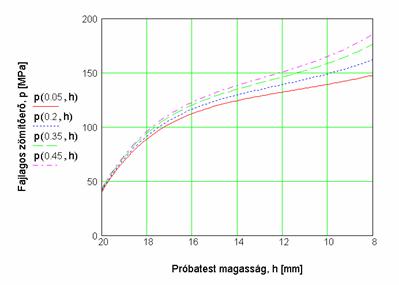
8.1.2 ábra

Súrlódás hatása a huzal- és rúdhúzás fajlagos alakítóerő szükségletére és a húzógyűrű optimális félkúpszögére

Kúpos csatornában végzett huzal- vagy rúdhúzás fajlagos erőszükséglete

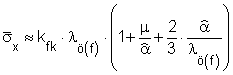
összefüggéssel határozható meg (lásd: [2]), ahol:

 - a a húzás során, a kilépő keresztmetszet felületegységére működtetendő húzóerő,

k_fk - a kúpos csatornában lévő anyag közepes alakítási szilárdsága,

 - a kúpos csatorna kilépő keresztmetszetében létrejövő összehasonlító alakváltozás,

 - a kúpos csatorna félkúpszöge, radiánban.

d_o = 3,6 mm belépő- és d_f = 3,2 mm kilépő átmérőjű húzógyűrűben CuZn36 anyagminőségű huzal húzásának fajlagos erőszükségletét szemlélteti a húzógyűrű félkúpszögének függvényében, m m m = 0,3 és m = 0,45-0s súrlódási tényezők esetén a 8.1.3 ábra szemlélteti. Az ábra szerint a kúpfal és az áramló anyag közötti súrlódási tényező növekedésekor növekszik az optimális félkúpszöghöz tartozó fajlagos erőszükséglet és maga az optimális félkúpszög is. Optimális félkúpszögnek a fajlagos húzóerő minimumához tartozó félkúpszöget tekintjük.

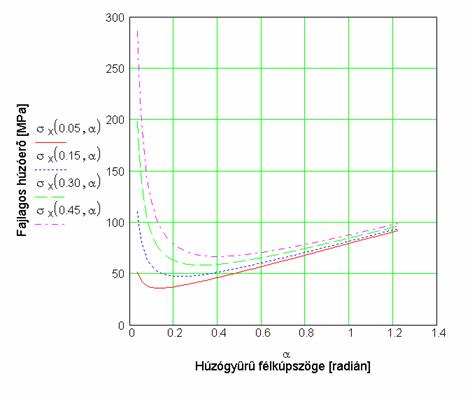
8.1.3 ábra

8.2 Súrlódási tényező meghatározása

A súrlódási viszonyok vizsgálatára, illetve a súrlódást jellemző mérőszámok meghatározására számos módszer ismert, mint például a:

szalaghúzó próba,

nyújtva hajlító próba,

gyűrűzömítő vizsgálat.

A mérési módszerek -mérési elvüket tekintve- lényegében két csoportba sorolhatók.

Az egyik csoportba tartozó eljárásoknál a képlékenységtan elméletének felhasználásával az adott alakítási modellre levezetett összefüggés(sek)ből állítható elő a súrlódás jellemzésére szolgáló mérőszám. Ezeknél lényegében a kisérleti alakítás végén kapott próbatest geometria hordozza a súrlódási viszonyokra vonatkozó információt. E csoportba tartozó módszerek klasszikus képviselője a nyújtva-hajlító próbával és a gyűrűzömítő vizsgálattal végzett súrlódási mérőszám meghatározás.

A másik csoportba tartozó eljárások közös jellemzője, hogy az alakítási modell szerszámozását úgy alakítják ki, hogy azon az F_n és F_s erő külön-külön mérhető legyen és a kettő felhasználásával határozzák meg m értékét (lásd szalaghúzó próba).

Meg kell jegyezni, hogy a második csoportba tartozó mérési módszereknél az erők pontos mérése bizonyos alakítási modelleknél (kúpos csatorna, zömítés) bonyolult feladat, viszont a súrlódási tényező értéke a mért erőkkel egyszerű összefüggésekkel határozható meg.

Az első csoportba tartozó módszerek méréstechnikailag viszonylag egyszerűek, de a súrlódási mérőszám az alakított próbatest képlékenységtani elemzésével levezetett bonyolult összefüggésekből fejezhető ki, vagy ha ez nem lehetséges akkor numerikus módszerek alkalmazásával állítható elő.

Szalaghúzó próba

A szalaghúzó próba a legegyszerűbb kisérleti módszer a súrlódási tényező meghatározására. A mérés elvi elrendezését a 8.2.1 ábra szemlélteti. Két szorító betét között -amelyeket F_n erő szorít össze- a szalag húzásához szükséges erő a:

összefüggéssel, az ebből kifejezett m súrlódási tényező pedig a:

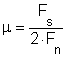
összefüggéssel számítható.

A kisérlet során biztosítani kell a szalag egyenletes, kis sebességgel végzett húzását, közben mérni kell az F_n és F_s erőket. E kisérlet során a szalag rugalmas alakváltozásállapotban van. A vizsgálat során különböző anyagminőségű lemezt és szorító betétet (például rugalmas gumi, vagy poliuretán) is lehet alkalmazni

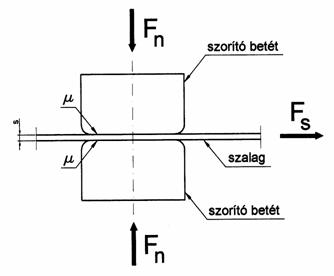
8.2.1 ábra

Nyújtva-hajlító próba

A nyújtva-hajlító próba elvi vázlata a 8.2.2 ábrán látható.

A két végén elmozdulásmentesen befogott szalag képlékenyen nyúlik, ebből következően elmozdulást végez a hajlító henger felületén. Az 1-es és 2-es helyeken a szalagban (a súrlódás következtében) eltérő nagyságú tangenciális irányú húzófeszültségek ébrednek. Az s lemezvastagsághoz képest elegendően széles lemezt használva a kisérlethez a lemez alakváltozásállapota síkalakváltozásnak tekinthető, azaz b = b_o, ahol b_o a szalag alakítás előtti szélessége (a póbatest ábra síkjára merőleges mérete).

Az 1-es és 2-es helyeken mért lemezvastagság-csökkenésből, a lemezanyag folyásgörbéjének ismeretében a s és s feszültségek meghatározhatók. A kötélsúrlódás törvényének felhasználásával, ezek közötti kapcsolatot a:

összefüggés jellemzi, ahol: - az 1-es és 2-es hely között mérhető átfogási szög radiánban mérve.

Az előbbi összefüggésből a Coulomb-féle súrlódási tényező értékére a:

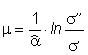
összefüggést kapjuk.

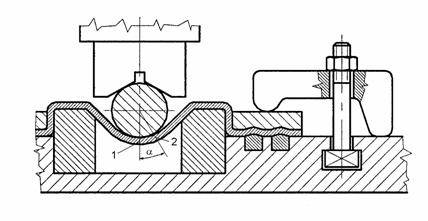
8.2.2 ábra

Gyűrűzömítő vizsgálat elve

A gyakorlatban egyszerű méréstechnikája miatt különös jelentősége van a gyűrűzömítő vizsgálattal végzett súrlódási tényező meghatározásnak.

A módszer azon a gyakorlati megfigyelésen alapszik, hogy egy hengeres gyűrűt két síklap között axiális irányban h_o-ról "h" magasságra zömítve, a külső és belső átmérőjének megváltozása a szerszámmal érintkező felületek között ébredő súrlódás nagyságától függ, melyet a 8.2.3 elvi ábra szemléltet.

Ha a súrlódási tényező kicsi, akkor a gyűrű belső átmérője gyakorlatilag nem változik (esetleg kis mértékben nő), a külső átmérő jelentősen növekszik. Kedvezőtlen súrlódási viszonyok mellett a külső átmérő kevésbé nő, a belső átmérő csökken. Tehát a "h" magasságra zömített gyűrű geometriája hordozza a súrlódási viszonyokra vonatkozó információt.

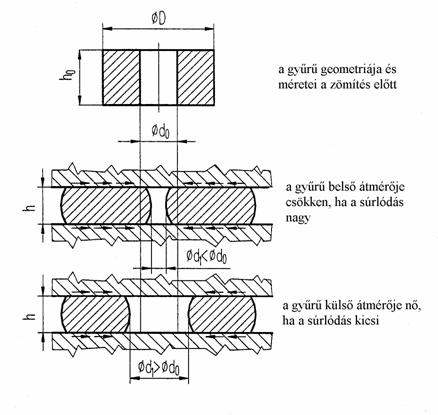
8.2.3 ábra

Az alakváltozási folyamat analízisével a súrlódási mérőszámok a geometriai méretváltozásból előállíthatók.

Gyűrűzömítő vizsgálat méréstechnikája

A próbatest kiinduló és zömítés utáni geometriáját a 8.2.4 ábra szemlélteti.

A zömítés során a külső és belső átmérők -a nyomólapok közelében lévő anyagrészek radiális irányú mozgásának súrlódás okozta fékezettsége miatt- hordósodnak.

A h zömítési magassághoz tartozó idealizált (hordósodás nélküli állapothoz tartozó) geometriai méretek, valamint a semleges (helyben maradó) réteg helyzete a térfogatállandóság felhasználásával határozható meg.

A D_k idealizált külső átmérő a viszonylag jól mérhető D^' és D^'' átmérőkből a

összefüggéssel számítható.

A teljes térfogatra felírt térfogatállandóságból az r_b idealizált belső sugarat kifejezve a

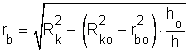
összefüggést kapjuk.

A semleges réteg sugarát az r > r_o térfogatrészre felírt térfogatállandóságból kifejezve jutunk a

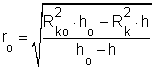
összefüggéshez.

A gyűrű feszültség- és alakváltozás analízise során, a semleges réteg két oldalára felírható s_r(r) és s_z(r) feszültségfüggvények felhasználásával meghatározható az "m" Kudo - féle súrlódási szám és a "m" Coulomb - féle súrlódási tényező.

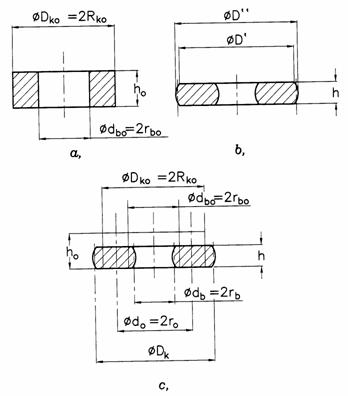
8.2.4 ábra

Kudo-féle súrlódási szám meghatározása

Az "m" súrlódási szám abból a feltételből határozható meg, hogy a semleges réteg helyén (r = ro helyen) a radiális irányú feszültségek értéke megegyezik, azaz: s_r1(r_o) = s_r2(r_o),

A feszűltségfüggvények helyettesítése és rendezés után, az "m" súrlódási számra kapott összefüggésben csak a sajtolt gyűrű geometriai méretei (r_k, r_b, h) és a semleges réteg (r_o) sugara szerepel:

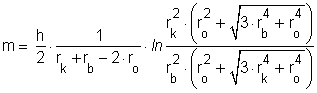
Coulomb-féle súrlódási tényező meghatározása

A m Coulomb-féle súrlódási tényező abból a feltételből határozható meg, hogy a zömített darab félmagasságában (a h/2 helyen), a semleges réteg jobb- és baloldalára levezetett axiális irányú feszültség értéke az r = r_o helyen megegyezik, tehát s_z1(r_o) = s_z2(r_o), ahol

s_z1  a

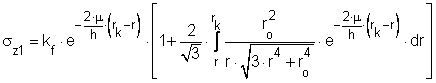
s_z2 a

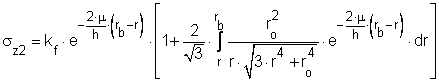
összefüggésekkel határozható meg.

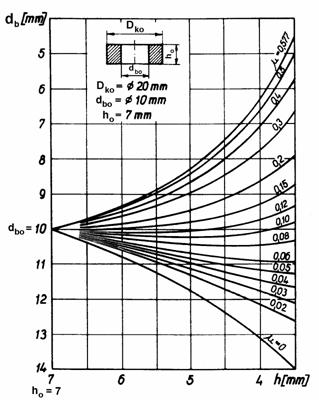
8.2.5 ábra

A kapott s_z1  s_z2 egyenletben szereplő integrálok zárt alakban nem oldhatók meg, így az adott zömítési magassághoz tartozó gyűrűméretekre numerikus integrálással lehet a feladatot megoldani.

A mért geometriai méretekből a m súrlódási tényező gyors meghatározását teszi lehetővé a Burgdorf által a fenti egyenlet alapján szerkesztett nomogram, amely a 8.2.5 ábrán látható és az ott feltüntetett kiinduló méretekkel rendelkező gyűrű zömítése során alkalmazható a súrlódási tényező meghatározására.

9 Alakíthatóság

Az alakíthatóság a fémek képlékeny alakváltozási képességét számszerűen fejezi ki a repedés, illetve a törés bekövetkeztéig elviselt összehasonlító alakváltozás mérőszámával.

Azt az összehasonlító alakváltozást, ameddig az alakítás káresemény (pl. képlékeny instabilitás, repedés, törés) bekövetkeztéig folytatható a képlékenyen alakított darabon határalakváltozásnak, az esemény bekövetkeztéhez tartozó állapotot pedig határállapotnak nevezik. E határállapot pontos ismerete nélkül korszerű alakítástechnológiai CAD -rendszer nem hozható létre.

Meg kell jegyezni, hogy az alakítási határállapotnak van egy tágabb értelmezése is. A további alakítás számára ugyanis nemcsak az alakváltozóképesség kimerülése jelenthet korlátot, hanem számos egyéb tényező is. Például azok a körülmények amikor a káresemény az alakváltozási zónán kívül következik be (pl. fenékleszakadás, ráncosodás mélyhúzásnál, kihajlás zömítésnél, felzömülés redukálásnál, az alakítószerszám korlátozott teherbíró képessége, vagy a kenőképesség kimerülése a kent felület nagymértékű megnövekedése miatt).

A továbbiakban az alakíthatósági határállapot elsőként említett szűkebb értelmezését használjuk.

Alakíthatósági határállapot értelmezése

Fémek képlékenyalakításakor a törésig elviselt képlékeny alakváltozást befolyásoló tényezőket a

elvi összefüggés szemlélteti.

A T[ C] hőmérséklet befolyásoló hatása közismert. Az alakítási hőmérséklet növelése az alakítási szilárdságot csökkenti, az alakíthatóságot növeli. Ezt a körülményt régen kihasználják az alakíthatóság növelésére (lásd: kovácsolás).

Az összehasonlító alakváltozás-sebesség állapot hatása kevésbé ismert. Gyakorlati jelentősége a melegalakítás körülményei között jelentős. Hatását hidegalakításnál legtöbbször nem veszik figyelembe.

A feszültségállapot alapvetően meghatározó paramétere a törésig elviselt alakváltozásnak. Törés-, illetve repedésmentes alakítás szempontjából döntő jelentőségű, hogy az adott eljárás során milyen a feszültség- és alakváltozásállapot a képlékeny zónában.

Az újabb kutatások során bebizonyosodott, nem csak a törés pillanatában fennálló feszültségállapot döntő az alakíthatóság szempontjából, hanem a deformáció teljes folyamata alatt bekövetkező feszültségállapot, illetve a hatására létrejövő alakváltozásállapot, vagy más szóval a deformációtörténet is.

A negyedik befolyásoló paraméter az "A"-val jelölt, az anyagszerkezet hatását kifejező függvény. Az "A" paraméter magába foglalja mindazokat az anyagjellemzőket (kristályszerkezet, szemcseszerkezet, szövetszerkezet, ötvözők, hőkezeltségi állapot stb.) amelyek az alakításra kerülő anyagot jellemzik.

A törésig elviselt alakváltozás előbb felírt elvi képlete általános esetre nem ismert és eddig elméletileg sem sikerült levezetni.

A legtöbb képlékenyalakító technológiánál nem szükséges az alakíthatósági határ problémáját ilyen általánosan vizsgálni. Megbízható következtetés vonható le az alakíthatósági határra vonatkozóan megfelelő számú egyszerű kisérlet eredményéből is.

Az alakíthatósági határállapot a két fő alakítási módnál -a lemez- és térfogatalakításnál- jól elkülöníthető. Az alakíthatósági határ megállapítására szolgáló kisérletek mérési eredményeit diagramban rögzítik, amelyet térfogatalakításnál alakíthatósági diagramnak, a lemezalakításnál alakíthatósági határgörbének neveznek.

Alakíthatósági diagram

Az alakíthatósági diagram a törésig elviselt összehasonlító-alakváltozást

tartalmazza a feszültségállapot-mutató függvényében:

adott anyagminőségre és anyagszerkezetre,

adott hőmérsékleten és

adott összehasonlító-alakváltozássebesség mellett.

A fentiekből következik, hogy a diagram független változója a feszültségállapottal kapcsolatos mennyiség, a többi befolyásoló tényezőt csak mint paramétert veszi figyelembe.

Az alakíthatósági diagram jellegzetes megjelenési formáját szemlélteti a 9.1 ábra.

A k feszültségállapot-mutató, a képlékeny állapotban lévő térfogat valamely pontjában a s_m középfeszültség és az adott pontban érvényes k_f alakítási szilárdság ismeretében határozható meg a

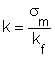
képlettel.

A középfeszültség

összefüggéssel számítható, ahol: I a feszültségtenzor első skalárinvariánsa.

A 9.1 ábrából látható, a feszültségállapot-mutató értékének csökkenésekor (többtengelyű nyomófeszültség állapot) a törésig elviselt összehasonlító-alakváltozás értéke nő.

Az alakíthatósági diagram összetartozó k_f - értékeit különböző feszültségállapot mellett (szakítás, csavarás, zömítés) törésig végzett alakítással kisérletileg határozzák meg. A mért pontsorra leggyakrabban a:

alakú függvényt illesztik, ahol: a - anyagtól függő állandó.

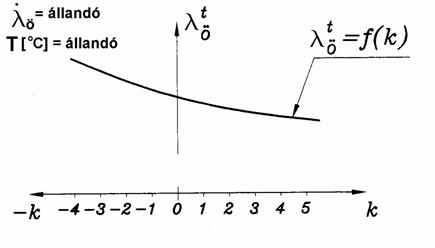
9.1 ábra

Alakíthatósági határállapot beépítése a képlékenyalakító technológia tervezőrendszerébe

Az alakíthatósági határállapot képlékenyalakító technológia tervezőrendszerbe való beépítésének két feltétele van.

Az első az alakított anyag törésig elviselt összehasonlító alakváltozásának ismerete a feszültségállapot-mutató függvényében, vagyis az alakíthatósági diagram ismerete az adott alakítási hőmérsékleten és deformációsebesség mellett.

A második a technológiai folyamat feszültségi és alakváltozási állapotának ismerete az alakítási folyamat teljes tartományában.

Ezek ismeretében meghatározható az anyag képlékenységi tartalékának kihasználtsági foka (y). Továbbá lehetőség nyílik az alakíthatóság szempontjából optimális technológiai paraméterek (pl. szerszámgeometria, alakítási hőmérséklet, szerszámsebesség, stb.) megállapítására.

Alakíthatósági határgörbe

A lemezek hidegalakításának területére dolgozta ki Keeler és Goodwin a lemezek határalakváltozásának elméletét. Az elmélet lényege: lemezek sík feszültségi állapotban végzett alakításakor, a feszültségállapot hatására -a károsodás helyén- a lemez síkjában létrejövő valódi nyúlások folytonos határgörbét alkotnak. Az alakítási határgörbe pontjait tehát a károsodási helyen a lemez síkjában mért összetartozó legkisebb és legnagyobb valódi nyúlások határozzák meg. A határgörbe alatti -összetartozó- legkisebb és legnagyobb valódi nyúlásértékeknél károsodás nem keletkezik a lemezben, a határgörbe feletti értékeknél igen.

A károsodás bekövetkezését kétféle módon szokás jellemezni:

a törés (repedés) megjelenésével,

a képlékeny instabilitás megjelenésével.

A képlékeny instabilitás azt jelenti, hogy a további alakításnál az alakváltozás nem a lemez teljes térfogatában megy végbe, hanem csak egy szűk térfogatrészben, vagyis a helyi kontrakció kialakulásának megjelenésével hozható kapcsolatba. Mivel a képlékeny instabilitás kialakulása mindig megelőzi a törést, ezért a képlékeny instabilitáshoz kötött határalakváltozás szigorúbb korlátot jelent, mint a töréshez kapcsolt határ.

Míg a törés megjelenésével jellemzett határalakváltozást csak kisérletileg lehet meghatározni, addig a instabilitási határt jelentő görbe elméleti úton is számítható.

Az alakítási határgörbe (Keeler - Goodwin diagram) jellegzetes megjelenési formáját szemlélteti a 9.2 ábra, feltüntetve a töréshez és a képlékeny instabilitáshoz tartozó határgörbéket. A térfogatalakításhoz hasonlóan, a diagram közvetve a feszültségállapot függvényében kezeli az alakíthatósági határt. A hőmérséklet, az alakváltozás-sebesség, az anyagminőség, az anyagszerkezet paraméternek tekinthető.

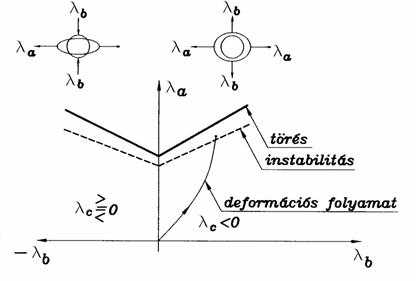
9.2 ábra

Az alakíthatósági határgörbe használatához ismerni kell a tervezett képlékenyalakító technológiával alakított lemez kritikus helyein a lemez síkjában fellépő legnagyobb és legkisebb valódi nyúlás értékeket. Az összetartozó értékeket az adott lemez alakítási határgörbéjét tartalmazó koordináta-rendszerben kell felmérni. Amennyiben a kapott pont(ok) a határgörbe alatti tartományban helyezkedik el, akkor a tervezett technológiával nagy valószínűséggel selejtmentes gyártás valósítható meg.

10 Hideg-, félmeleg- és melegalakítás fogalma, jellemzői

A képlékenyalakító technológiák rendszerezésének egyik -gyakran alkalmazott- rendező elve az alakítás hőmérséklete.

A hideg- és melegalakítás szerinti felosztás régóta ismert, jóllehet a technológiai, illetve fémtani megfogalmazás szerinti definíciók eltérően fogalmazzák meg azok jellemzőit.

Technológiai szempontok szerinti megitélés:

a hőközlés nélkül -vagyis szobahőmérsékleten végzett- alakítást tekinti hidegalakításnak és az alakítás előtt, vagy közben végzett hőközléssel történő alakítást melegalakításnak.

A fémtani megfogalmazás szerint:

az újrakristályosodási hőmérséklet (T_rekr) felett végzett alakítás a melegalakítás, a megújulási hőmérséklet (T_m) alatti hőmérsékleten végzett alakítás a hidegalakítás.

Például a 800 C-on végzett volfram huzal gyártás fémtani megitélés szerint hidegalakítás, mert ez alatta van a volfram megújulási hőmérsékletének. Technológiai megitélés szempontjából viszont melegalakítás, mert a szerszámanyagok, berendezések hőigénybevétele miatt hasonló nehézségek merülnek fel mint például az acél melegalakításánál.

A 10.1 ábrán látható elvi diagram a fémtani felosztást szemlélteti, a hidegen alakított, majd különböző hőmérsékletre hevített darab mechanikai tulajdonságainak (szilárdság, keménység, alakíthatóság), szemcseméret és maradófeszültségek ábrázolásával.

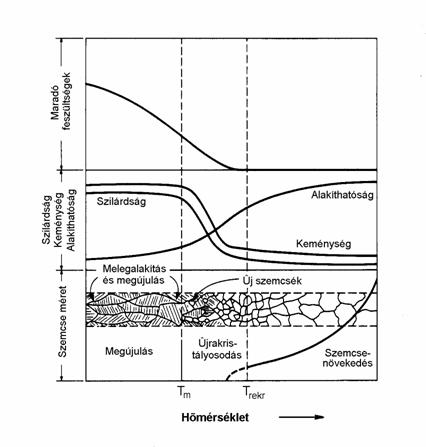
10.1 ábra

A hideg- és melegalakítás közötti hőmérséklettartomány (T_m<T<T_rekr) az a zóna, amelyen belül megindulnak a teljes újrakristályosodást megelőző folyamatok. Elvileg ez a hőköz tekinthető a félmeleg-alakítás hőmérséklettartományának.

A továbbiakban jellemezzük a hideg-, félmeleg- és melegalakítás hőmérsékletartományában végzett alakítás előnyeit, hátrányait.

A fentiekből következik, hogy a hideg-, félmeleg- és melegalakítás nem egy meghatározott hőmérsékletet, hanem fémtől függően más és más hőmérséklettartományt jelent.

Hidegalakítás

A fémek képlékeny alakváltozásának folyamata a diszlokációelmélettel írható le.

A polikrisztallin fémek hidegalakítás előtt homogén, izotróp testként kezelhetők. Szemcsézetük poligonális, melyet a 10.2 ábra szemléltet. Hidegalakítás után a fém izotrópiája megszűnik. Az alakváltozás során minden kristály működő csúszási síkja és iránya igyekszik elfordulni a legnagyobb főnyúlás irányába, s az alakváltozás mértékének növekedésével egyre tökéletesebb rendezettség alakul ki. Az alakított fém hidegalakítás után is polikrisztallin szemcsézetű, de a benne fellépő rendezettség miatt (az alakítás irányába megnyúlt, rendezett szemcsézet) a mechanikai tulajdonságai (pl. R_p0,2, R_m, Z, A) attól függnek, hogy a vizsgálathoz felhasznált próbatest az alakítás irányához képest milyen irányból lett kivéve.

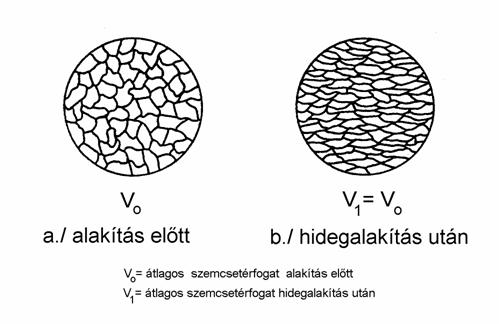
10.2 ábra

Az alakítás irányába kialakult rendezettség az alakítási textúra. Következménye a mechanikai tulajdonságok irányfüggése, vagyis az anizotrópia.

A hidegalakítás során megváltozott tulajdonságok az alakítás után is megmaradnak. E változások megszüntetése, az eredetihez közelálló jellemzők visszaállítása újrakristályosító izzítással lehetséges. Ennek során -öndiffúzióval, csírából- az alakítás során eltorzult szemcsézet kristályhatárairól kiindulva, új poligonális, arányos méretű szemcsék keletkeznek, amelyekben a diszlokációsűrűség közel az alakítás előtti értékre csökken.

A rekrisztallizáció utáni szemcsék térfogata:

az alakváltozás mértékétől,

az újrakristályosító izzítás hőmérsékletétől és

idejétől függ.

A hidegalakítást követő hevítés hatását az alakított fém mechanikai tulajdonságaira a 10.1 ábrán látható elvi digram szemlélteti.

A képlékeny hidegalakítás előnyei:

A képlékeny hidegalakítással gyártott munkadarabok felületi minősége jó és bizonyos feltételek megléte esetén lényegesen jobb felületi minőséggel lehet gyártani, mint más technológiákkal.

A képlékeny hidegalakítással gyártott darabok átmérő méretei IT6-IT9 méretpontossággal gyárthatók.

Meghatározott alakváltozás létrehozásához szükséges energia kisebb, mint ha ezt melegalakítással hozták volna létre.

Az alakítási keményedés kihasználásával növelt szilárdságú alkatrészt lehet gyártani. Ezzel ötvözött acélok felhasználása és a szilárdságnövelés létrehozásához szükséges hőkezelési technológia takarítható meg.

Az előnyök felsorolásával egyidejűleg meg kell említeni a képlékeny hidegalakítás korlátait is, amelyek a következők:

Hidegalakítással gazdaságosan elsősorban a kis C- és Si tartalmú ötvözetlen acélok alakíthatók. A növekvő ötvözőtartalom jelentősen növeli az alakítási szilárdságot és így az alakítási ellenállást is. Ez jól megfigyelhető az ötvözetlen C15 és a kb. 1% Cr-tartalmú BC3 acél folyási görbéin. A két acél széntartalma kb. ugyanannyi, de a BC3 ötvözőtartalma miatt az alakítási szilárdsága, keményedő képessége lényegesen nagyobb mint a C15-ös acélé (10.3 ábra)

Hidegalakítással -közbenső lágyítás nélkül- az elérhető alakváltozás kisebb, mint a melegalakítással megvalósítható érték.

Bonyolult alakú, sarkos alkatrészek gyártásánál az alakító üreg kitöltése nehezen biztosítható, mert vagy az anyag alakíthatósága merül ki, vagy a szerszámterhelések növekednek a szerszámacélokra megengedhető érték (kb. 2000-2500 N/mm²) fölé.

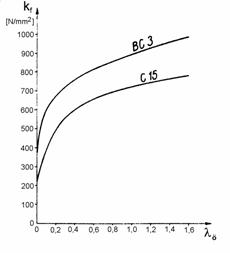
10.3 ábra

A hidegalakításnál a felsorolt nehézségek leküzdésére elvileg a következő lehetőségek kínálkoznak:

Új szerszámanyagok kifejlesztésével (amelyek nagyobb szilárdságúak és szívósabbak), a szerszámanyagok terhelhetősége növelhető.

Olyan technológiai folyamatokat kell megvalósítani, amelyekben a hidegalakítást előalakítással kombinálva, a hidegalakítás során csak kismértékű alakváltozást valósítanak meg és így a hidegalakítás készrealakító technológiaként szerepel.

Megoldásként kínálkozik az is, hogy az alakításhoz szükséges energia egy részét a munkadarab melegítésével közlik a darabbal. Ezen alapulnak a félmelegalakítási technológiák és a gyakorlatban viszonylag egyszerűen megvalósíthatók.

A hőmérséklet növelésének hatását az alakítási szilárdságra (k_f), a határalakváltozásra (törésig elviselt összehasonlító alakváltozásra) és a revésedés mértékére (Fe_v) acél esetén a 10.4 ábrán látható elvi vázlat szemlélteti.

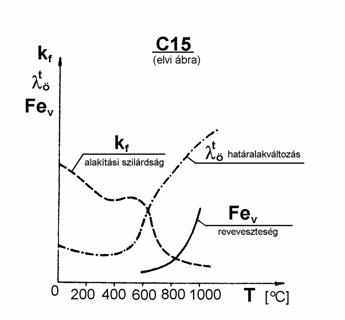
10.4 ábra

Az ábrán megfigyelhető, hogy a hőmérsékletet addig érdemes növelni, amíg a nagyobb mértékű revésedés nem indul meg. A feldolgozandó acélanyagtól függően ez a hőmérséklettartomány kb. 550-700 C között van. Ezzel a módszerrel csökkenthető az alakítási ellenállás, a hidegalakításnál megjelenő értékekhez képest. A csekély mértékű revésedés miatt pedig lényegesen jobb a felületi minőség, mint melegalakításnál.

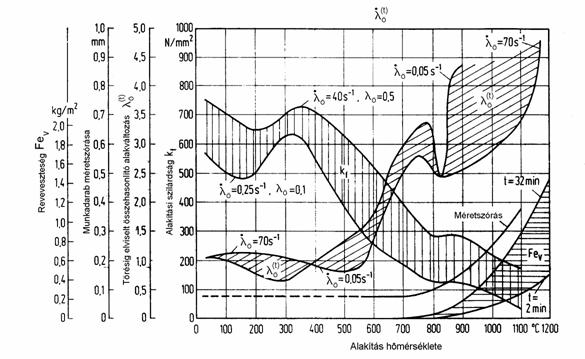
A 10.4 elvi ábrával szemben a 10.5 ábra a C15-ös anyag mért fenti jellemzőit szemlélteti a hőmérséklet függvényében. Az alakítási szilárdság (k_f) változását és összehasonlító alakváltozás-sebességhez tartozóan, a törésig elviselt összehasonlító alakváltozást () pedig és összehasonlító alakváltozás-sebességhez tartozóan szemlélteti. Ezeken kívül feltünteti a t=2 perces és t=32 perces hőntartás során létrejövő reveveszteséget (Fe_v), valamint a készre alakított munkadarabok méretszórásának elvi változását.

Félmeleg-alakítás

A félmeleg-alakítás hőmérséklettartománya elméletileg a megújulási (T_m) és rekrisztallizációs (T_rekr) hőmérsékletek között jelölhető ki. A gyakorlatban, acéloknál a felső határát az intenzív revésedés kezdő hőmérséklete korlátozza.

A félmeleg-alakítás előnyei:

A növekvő alakváltozóképesség és a csökkenő alakítási szilárdság miatt javul az üregtöltés.

Nagyobb ötvözőtartalmú acélok is folyathatók, mint pl. saválló, hőálló acélok.

Azonos alakítógép terheléssel nagyobb tömegű acél alakíthatók, mint hidegalakítással.

10.4 ábra

A félmeleg alakításnál a következő nehézségek fellépésével kell számolni:

Az alakítás során -folyamatos üzem esetén- az alakító szerszám aktív elemei is felmelegednek kb. 200-300 C-ra, ezért drágább, általában Mo-ötvözésű gyorsacélt kell választani szerszámanyagnak.

A technológia tervezéshez szükséges alapadatok ismerete -az alakítási szilárdság hőmérséklettől és deformációsebességtől való függése- elengedhetetlenül szükséges, amelyek a vonatkozó irodalomban többnyire hiányosan állnak rendelkezésre.

Kenési problémák lépnek fel, mert az acélok hidegfolyatásánál jól bevált foszfátozás nem ad megoldást, mert az acél felületén kialakított cinkfoszfát réteg 200-300 C-on szétbomlik és kenőanyag-tárolóképessége megszűnik. Az ugyancsak jól bevált molibdéndiszulfid (MoS₂) és wolframdiszulfid (WS₂) kenőanyagadalékok a félmelegalakítás hőmérsékletén trioxiddá alakulnak. A kenőanyagként használt grafitpor 450-480 C-on CO₂-vé alakul. Hasonlóképpen csődöt mondanak az olajbázisú kenőanyagok, mert a félmeleg-alakítás hőmérsékletén már kokszosodnak.

A munkadarabok felhevítése a félmeleg-alakítás hőmérsékletére rendszerint indukciós hevítéssel történik. A hevítőberendezések gyártósorba való telepítését el kell végezni .

Melegalakítás

Melegalakításkor az alakváltozás okozta keményedés és -az újrakristályosodási hőmérsékletnél (T_rekr<T) nagyobb alakítási hőmérséklet miatt- az újrakristályosodás alakítás közben -illetve közvetlenül utána, még meleg állapotban- végbemegy. Következésképpen a fém az alakítás után közel az eredeti (alakítás előtti) tulajdonságokkal rendelkezik. A keményedés az alakítás következtében itt is fellép, de ezt kisebb-nagyobb késéssel követi az újrakristályosodás, ezért a változások a késztermékben lényegében nem észlelhetők.

Meg kell jegyezni, a keményedés az alakváltozás közvetlen velejárója, tehát azonnal létrejön (nincs időszükséglete). Ezzel szemben az újrakristályosodás (lágyulás) időigényes folyamat, a másodperc tört részétől több percig, esetleg óráig tartó folyamat lehet. Ezért csak bizonyos feltételek teljesülése esetén jelenthető ki, hogy a felkeményedés jelensége melegalakításnál nem észlelhető.

A melegalakítás előnyei:

Az alakítandó darab anyagának az alakítási szilárdsága a melegalakítás hőmérsékletén a legkisebb (lásd: 10.5 ábrát).

Képlékenyen nagy ötvöző tartalmú acélok is feldolgozhatók.

Teljes-, vagy résztérfogatra kiterjedő alakítással nagyobb tömegű munkadarabok alakíthatók mint hideg-, vagy félmeleg-alakításnál.

Az üregtöltő képesség kedvezőbb, ezért tagoltabb, bonyolultabb geometriájú üregek feltöltése is elvégezhető, mint hideg-, vagy félmeleg-alakításnál.

A melegalakítás hátrányai:

Az alakítási energia egyrészét hőenergia formájában viszik be a darabba, amely jelentős gyártóeszköz- (pl. hevítő berendezés) és költségtöbbletet (energia költség) jelent.

A melegalakítás hőmérsékletén is megfelelő szilárdságú, nagy ötvöző tartalmú szerszámacélokkal oldható meg a szerszámozás.

Acélok melegalakítási hőmérsékletre hevítésénél jelentős revésedéssel kell számolni. Revés előgyártmány revétlenítését el kell végezni, mert revésen alakítva fokozott szerszámkopást okoz és a kész darabon -a további megmunkálhatóság, valamint esztétikai okok miatt- nem engedhetők meg revemaradványok. Megoldás lehet a védőgázas környezetben történő alakítási hőmérsékletre hevítés. Ezek a kiegészítő technológiai műveletek további költségnövekedést okoznak.

A megfelelő súrlódási viszonyok biztosítása a melegalakítás hőmérsékletén fokozott kenéstechnológiai problémákat jelent. A magas hőmérsékleten stabil és megfelelő kenőképességgel rendelkező kenőanyagok korlátozottan állnak rendelkezésre és drágák.

Az alakított darabok méretszórása az alakítási hőmérséklet növelésével növekszik, azaz a gyártási pontosság csökken (lásd: 10.5 ábrát).

4. Definíciók

Alakítási szilárdság:

Anizotróp:

Anyagtörvény:

Diszlokációelmélet:
Folyásgörbe:

Fajlagos alakítóerő:

Félmeleg-alakítás:

Félmeleg-alakító technológiák:

Feszültségi állapot:

Főfeszültségek:

Gépipari képlékenyalakító technológiák:

Hidegalakítás:

Hidegalakító technológiák:

Homogén:

Izotróp:

Képlékenység:

Képlékeny zóna:

Képlékenyalakítás:

Képlékenységi feltétel:

Képlékenységtan:

Kohászati képlékenyalakító technológiák:

Lemezalakító technológiák:

Megújulás:

Megújulási hőmérséklet:

Melegalakítás:

Melegalakító technológiák:

Összehasonlító alakváltozás:

Összehasonlító alakváltozás-sebesség:

Összehasonlító feszültség:

Szuperképlékenység:

Térfogatalakító technológiák:

Újrakristályosodási hőmérséklet:

Valódi, vagy logaritmikus nyúlás:

Alakítási szilárdság (k_f):

az alakított anyag mindenkori folyáshatára, egytengelyű feszültségállapotban az állapothatározó paraméterek (összehasonlító alakváltozás, összehasonlító alakváltozássebesség, hőmérséklet) adott értékei mellett.

Adott anyagminőség képlékenyen alakváltozó zónájának valamely pontjában az alakítási szilárdság függvénye a pont pillanatnyi:

- összehasonlító alakváltozásának (),

- összehasonlító alakváltozássebességének ([1/s]),

- hőmérsékletének (T [ C]), azaz:

k_f = f (,[1/s], T [ C])

Anizotróp:

különböző irányokban eltérő tulajdonságokkal rendelkező anyagi rendszer.

Anyagtörvény:
az az összefüggés, amely megfogalmazza az anyag adott pontjában ébredő feszültségállapot következményeként létrejövő alakváltozásállapotot.

Fémek rugalmas alakváltozás tartományában az anyagtörvényt az általános Hooke-törvény írja le.

A rugalmas - képlékeny alakváltozás tartományban -ahol a képlékeny alakváltozások nagyságrendje megegyezik az azt megelőző rugalmas alakváltozások nagyságrendjével- az anyagtörvény például a Pradtl - Reuss egyenletekkel fogalmazható meg.

A nagy maradó alakváltozások tartományában (ahol a létrejövő képlékeny alakváltozások nagyságrenddekkel nagyobbak mint az azokat megelőző rugalmas alakváltozások) például a Mises-anyagtörvény alkalmazható.

Diszlokációelmélet:

A fémek képlékeny alakváltozása során a kristálysíkok egymáson több rácsállandónyi távolságra elcsúsznak anélkül, hogy az atomok közötti kötés megszakadna. A rácssíkok egymáshoz képest végzett elmozdulása irreverzibilis folyamat, mert a terhelés megszűnése után nem kerülnek az eredeti (kiinduló) helyzetükbe.

A valóságos kristály rácshibákat, például diszlokációt tartalmaz. A diszlokációkat tartalmazó kristály rácssíkjainak egymáshoz képesti eltolása lényegesen kisebb t csúsztatófeszültséget igényel, mint az ideális, rácshibát nem tartalmazó kristályrács esetén.

A rácssíkok elmozdulásának következményeként a diszlokációk mozgásra kényszerülnek, találkozásukkor reakcióba lépnek egymással. A reakció eredménye lehet, hogy két diszlokáció kioltja egymást, de bekövetkezhet a két diszlokáció blokkolódása, azaz mozgásképtelenné válása. Ezek a folyamatok a hidegen alakított fém felkeményedéséhez vezetnek.

Folyásgörbe:

adott anyagminőségű fém alakítási szilárdságának változása az összehasonlító alakváltozás függvényében, adott állandó alakítási hőmérsékleten és összehasonlító alakváltozás-sebesség mellett.

Fajlagos alakítóerő:

az alakított darab (technológia által meghatározott) felületén, az alakváltozás megindításához, illetve folyamatos fenntartásához felületegységenként működtetendő erő.

Félmeleg-alakítás:
a szobahőmérsékletnél magasabb hőmérsékleten végzett alakítás, amelyen az alakítási szilárdság csökkenése jelentős mértékű, de a revésedés (felület minőség romlása) még nem számottevő. A kenési problémák is kisebb mértékűek mint a melegalakítás hőmérsékletén végzett alakító eljárásoknál.

Félmeleg-alakító technológiák:

azok a képlékenyalakító eljárások, amelyek az alakítást az újrakristályosodási hőmérséklet közelében végzik. Tulajdonképpen kompromisszumos megoldásnak tekinthetők, mert a hőmérséklet növelése az alakítás erőszükségletét jelentősen csökkenti a hidegalakításhoz képest, viszont a melegalakítás hőmérsékleténél lényegesen alacsonyabb alakítási hőmérsékleten a revésedési folyamat elmarad, ezért munkadarab felületi minősége lényegesen jobb mint a melegalakítással gyártott daraboké. A szerszám és a munkadarab kenési problémái is egyszerűsödnek a melegalakító eljárásokhoz képest.

Feszültségi állapot:
a külső erőkkel terhelt darab valamely tetszőleges pontján átmenő, három egymásra merőleges sikon ébredő feszültségek összesége.

Főfeszültségek:
a külső erőkkel terhelt darab valamely tetszőleges pontján kitüntetett helyzetben átmenő, három egymásra merőleges sikon ébredő feszültségek összesége. A kitüntetett helyzet a síkok azon elhelyezését jelenti, amikor azokon csak normális irányú feszültségek ébrednek, csúsztató feszültségek nem.
Másképpen fogalmazva: a pont feszültségállapotát jellemző feszültségtenzor sajátértékei az alábbi relációnak megfelelően sorba rendezve: s ³ s ³ s

Gépipari képlékenyalakító technológiák:

a hagyományos gépipari üzemek gyártási folyamatába telepíthetők, a kész munkadarab kialakításához egymással kombinálhatók (pl. folyatott alkatrész bizonyos - folyatással nem gyártható - felületeinek kialakítása forgácsolással). E technológiák a zömítés, redukálás, folyatás süllyesztékes kovácsolás és a lemeztechnológiák nagy része (kivágás, lyukasztás, finomkivágás, mélyhúzás, hajlítás, stb.).

Hidegalakítás:

Fémtani szempontok szerinti megfogalmazás:

az alakított fém újrakristályosodási hőmérséklete alatti hőmérséklettartományban végzett alakítás.

Technológiai szempontok szerinti megfogalmazás:

az előgyártmány hőközlés nélkül (szobahőmérsékleten) végzett képlékenyalakítása.

Hidegalakító technológiák:

közé azokat a képlékenyalakító eljárásokat sorolják, amelyek olyan hőmérsékleten végzik az alakítást, amelyen az újrakristályosodási folyamatok az alakváltozással azonos időben nem mennek végbe. Az anyag keménysége az alakváltozással egyidejűleg növekszik, ezért az alakítás csak egyre nagyobb erővel folytatható. Az alakításnak határt szab az, hogy a fém alakváltozási képessége kimerül és a további alakváltozás helyett repedés vagy törés következik be. A hidegalakítás során létrehozható alakváltozás mértékének határa van, ami vagy a rendelkezésre álló erőtől (alakítógép névleges nyomóereje), vagy a repedések bekövetkezésének veszélyétől függ. A munkadarabon a további hidegalakítás akkor végezhető, ha a repedések megjelenése előtt az alakítást befejezzük, majd valamilyen regenerálási eljárással (lágyítás, újrakristályosítás) visszaállítjuk a fém lágyabb állapotát.

A hidegalakítást általában szobahőmérsékleten végzik. Előnye, hogy a munkadarab felülete kiváló minőségű. Hátránya a nagy erőigénye, amely az alakított darab tömegének növekedésével rohamosan nő.

Homogén:

minden pontjában azonos tulajdonságokkal rendelkező anyagi rendszer.

Izotróp:

minden irányban egyenértékű, azonos tulajdonságokkal rendelkező anyagi rendszer.

Képlékenység:

Képlékenységen a fémek és ötvözetek azon tulajdonságát értjük, hogy mechanikai igénybevétel hatására az alakjukat képesek megváltoztatni, az anyag kontinuitásának -folytonosságának- megmaradása mellett.

A jelentős maradó alakváltozásra képes fémeket képlékenynek tekintjük. Ezek ellentéte a rideg viselkedés. A rideg anyag, melynek alakváltozási képessége kicsi, gyakorlatilag nem, vagy csak igen kis mértékű alakváltozásra képes. Azokat az anyagokat tekintjük jól alakíthatónak, amelyek nagy maradó alakváltozást képesek elviselni a törés bekövetkezése előtt.

A képlékenység (alakíthatóság) nem abszolút tulajdonsága az anyagnak, hanem az állapottényezőknek is függvénye. Az állapottényezők: feszültségállapot, hőmérséklet, alakváltozássebesség állapot.

Képlékeny zóna:

amelyben a geometriai méretváltozás, azaz a képlékeny alakváltozás, ennek következményeképp az anyagi tulajdonságok megváltozása végbemegy. Az alakító technológiától függően kiterjedhet az alakított darab teljes térfogatára, vagy annak csak egy részére, valamint térfogata, elhelyezkedése az alakított darabban az alakítási folyamat során lehet állandó vagy változó.

Képlékenyalakítás:

olyan ipari gyártási módszer, amely kihasználva a fémek képlékeny alakváltozó képességét, megfelelő nagyságú külső, vagy belső erő(k) működtetésével az előgyártmány kezdeti alakját a kívánt geometriai formára változtatja úgy, hogy eközben az atomok közötti kötés nem szakad meg (repedés, törés) és térfogata állandó marad. Szinonímái: forgácsnélküli alakítás, forgácsmentes alakítás.

Képlékenységi feltétel:

az az összefüggés, amely megadja a feszültségek minden olyan kombinációját, amelynek fennállásakor a rugalmas alakváltozásállapot végetér, a képlékeny alakváltozás megindul.

Ezt az úgynevezett folyási függvény (f) fogalmazza meg. Képlékeny állapotban f = 0, rugalmas állapotban f < 0. Ideálisan merev, tökéletesen képlékeny anyagmodell esetén f > 0 fizikailag nem lehetséges.

Izotróp anyag esetén a képlékenységi feltétel: f(_ij, k) = 0, alakban írható fel,

ahol: _ij -a képlékeny zóna vizsgált pontjában a feszültségállapotot jellemző feszültségtenzor,

k - az adott pontban a képlékeny állapot létrejöttéhez tartozó anyagjellemző.

Anizotróp anyagok esetén a képlékenységi feltétel a Hill-féle anizotrópia paraméterek segítségével fogalmazható meg.

Képlékenységtan:
a rugalmasságtan mellett a szilárdságtan másik nagy részterülete, amely a szilárd testek viselkedésének törvényszerűségeit írja le nagymértékű maradó alakváltozások során.

Kohászati képlékenyalakító technológiákat:

a nagy anyag és energia igényük, valamint a gyártási hulladék újrahasznosítása, a szállítási, anyagmozgatási útvonalak minimálisra csökkentése miatt célszerű kohóművek közelébe telepíteni. Ezek közül a leggyakoribbak: a hengerlés, a rúd- és profilhúzás, a varratnélküli csőgyártás, a rúd- és profilsajtolás.

Lemezalakító technológiák:

közé azokat a képlékenyalakító eljárásokat sorolják, amelyek kiinduló terméke hengerelt lemez vagy szalag, vagyis olyan előgyártmány melynek egyik mérete (a vastagsága) nagyságrendileg kisebb mint a másik két irányú mérete. Az előállított termék síkszerű vagy vékony "héjjal" körülzárt üreges test. A lemezalakító technológiák többségénél a sikszerű előgyártmány lemezvastagsága gyakorlatilag nem változik.

Megújulás:

Megújulásnak nevezzük azt a jelenséget, amikor a fém hidegalakítása során megváltozott tulajdonságok az alakítás előtti tulajdonságok irányában változnak, a kristályszerkezet megváltozása nélkül.

Megújulási hőmérséklet:

Azt a T hőmérsékletet, amelyen a hidegalakítás során felkeményedett fém szilárdsága csökkenni kezd, -vagyis a fém kilágyulása megkezdődik- megújulási hőmérsékletnek (T_m) nevezzük. A T_m hőmérsékletnél kisebb hőmérsékleten izzítva a hidegalakítás során létrejött mechanikai tulajdonságok (pl. folyáshatár, keménység) változatlanok maradnak,

Melegalakítás:
Fémtani szempontok szerinti megfogalmazás:

az alakított fém újrakristályosodási hőmérséklete feletti hőmérséklettartományban végzett alakítás.

Technológiai szempontok szerinti megfogalmazás:

az előgyártmány hőközlés után, vagy közben (szobahőmérsékletnél magasabb hőmérsékleten) végzett képlékenyalakítása.

Melegalakító technológiák:

közé azokat a képlékenyalakító eljárásokat sorolják, amelyek olyan hőmérsékleten végzik az alakítást, amelyen az újrakristályosodási folyamatok az alakváltozással gyakorlatilag egyidejűleg mennek végbe. Az alakváltozást ez esetben elméletileg csak a kifejtendő erő korlátozza. Hátránya viszont, hogy a melegalakítás hőmérsékletén az acél munkadarab revésedik, ami a felületminőséget rontja.

Összehasonlító alakváltozás:

a képlékeny alakváltozásállapotban érvényes anyagtörvényből (Mises egyenletek) levezethető, az alakváltozás állapotot jellemző tenzor () elemeinek felhasználásával, az alábbi összefüggéssel számítható:

az alakváltozás mértékét jellemző skalár mennyiség.

Összehasonlító alakváltozás-sebesség:

az összehasonlító alakváltozás analógiájára, az alakváltozás-sebesség állapotot jellemző tenzor () elemeinek felhasználásával, az alábbi összefüggéssel számítható:

az alakváltozás-sebesség mértékét jellemző skalár mennyiség.

Összehasonlító feszültség:

az a -többtengelyű feszültségállapotot jellemző feszültségtenzor elemeiből számítható- feszültség, amely a képlékeny állapot létrejötte, illetve folyamatos fenntartása szempontjából azonos értékű az egytengelyű húzás körülményei között képlékeny állapotot létrehozó, illetve folyamatosan fenntartó feszültséggel.

Meghatározása a Mises egyenletekből levezethető:

összefüggéssel végezhető, ahol S_ij a vizsgált pontban érvényes feszültségtenzor deviátortenzora.

Szuperképlékenység:

bizonyos ötvözetek azon tulajdonsága, hogy melegen nem úgy viselkednek mint általában a polikristályos fémek, hanem inkább nagyviszkozitású folyadékként. Extrém nagy egyenletes nyúlás -a kezdeti jeltávolság többszörösére, esetleg tízszeresére történő megnyújtásának- elviselésére képesek, kontrakció vagy törés létrejötte nélkül.

A szuperképlékenység létrejöttének feltételei:

az anyag rendkívül finom szemcseszerkezete (1,4...7m), amely alakítás közben is változatlan marad,

az alakítás hőmérséklete tartományban legyen,

kis összehasonlító alakváltozás-sebességgel () történjen az alakítás.

Néhány szuperképlékeny tulajdonságokkal rendelkező ötvözetet, a hozzájuk tartozó alakítási hőmérséklettel és összehasonlító alakváltozás-sebességgel mutat be az alábbi táblázat.
                              

Térfogatalakító technológiák:

közé sorolják azokat a képlékenyalakító eljárásokat, amelyek kiinduló terméke öntött tuskó, vagy öntött előtermék, illetve különböző méretű és többnyire egyszerű keresztmetszetű (négyzet, kör, téglalap, hatszög) rúd, vagy buga. Az alakváltozási zónában az alakváltozási állapot általában térbeli, amely többtengelyű feszültségállapot hatására megy végbe. Az alakítás erőszükséglete viszonylag nagy. A gyártott termék általában tömör és térbeli kiterjedése háromdimenziós.

Újrakristályosodási hőmérséklet:

alatt azt a hőmérsékletet értjük, amelyen egy adott mértékű alakváltozással alakított fém egy óra alatt tökéletesen újrakristályosodik.

Nagymértékű alakváltozással alakított színfémek újrakristályosodási hőmérséklete a homológ hőmérsékletskálán a

képlettel fejezhető ki.

Homológ hőmérséklet, a Kelvin fokban kifejezett, valamely jellemző hőmérsékletnek a fém olvadáspontjára vonatkoztatott relatív értéke a

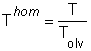
összefüggésnek megfelelően.

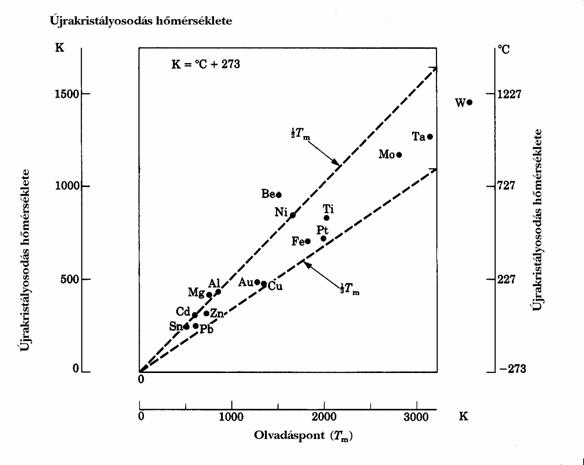
Újrakristályosodás homológ hőmérséklete tehát a

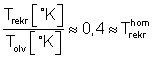
képlettel írható fel, amelyet a fenti ábra alapján értelmezhetünk. A diagram vízszintes tengelyén a fém olvadáspontja, baloldali függőleges tengelyén az újrakristályosodási hőmérsklete szerepel Kelvin fokban. Az ábrában szereplő fémek a 0,5 és 0,33 iránytangensű (T_rekr=0,33.0,5 T_olv) egyenesek között helyezkednek el, tehát a 0,4-es iránytangens közelítőleg az előbbi értékek átlagaként fogadható el.

Néhány fém olvadáspontja és a fenti képlettel számított rekrisztallizációs hőmérséklete az alábbi táblázatban látható.

Valódi, vagy logaritmikus nyúlás:
a méretváltozást (dl) a pillanatnyi jeltávra (l) vonatkoztatva kapjuk az elemi valódi, vagy logaritmikus nyúlást:

Az l_o - ról l₁ - re változott jeltáv esetén a valódi, vagy logaritmikus nyúlás mérőszáma:

Felhasznált irodalom:

[1] dr.Horváth L.: Képlékenyalakító technológiák elméleti alapjai

BMF jegyzet

[2] dr.Horváth L.: Képlékenyalakítási alapfeladatok elemzése a képlékenységtan

módszereivel BMF jegyzet

[3] K. Lange: Handbook of Metal Forming

McGraw-Hill, Dearborn, Michigan, U.S.A. 1985

[4] Kalpakjian: Manufacturing Processes for Engineering Materials

[5] Dr.Szabadíts Ö.- Dr,Ziaja Gy.: A félmeleg alakítás, mint a képlékeny hidegalakítás alkalmazási területének kiterjesztése

Hidegfolyatási Tanácskozás előadásai 1977 Szeptember 20.