Az SI-mértékrendszer

aLAPFOGALMAK

A fizika a jelenségeket mennyiségileg is jellemzi.

fizikai mennyiség = mérőszám mértékegység

Ahhoz, hogy egy mennyiséget mérni tudjunk, a mennyiségnek valamely rögzített értékét kell alapul választani. A mennyiségnek ezt az alapul választott, rögzített értékét mértékegységnek nevezzük.

A mérés a megmérendő mennyiség és a mértékegység összehasonlítása.

Az SI-mértékrendszer

System International (SI):

A fizika minden területére alkalmazható, nemzetközileg egységes mértékrendszer.

Alapmennyiségek:

Azok a fizikai mennyiségek, melyek más mennyiségekkel nem fejezhetők ki.

Az SI rendszer 7 alapmennyiséget használ. Ezek jele mellett meg kell ha 515e46f tározni a mértékegységet is (alap mértékegységek ), pontosan meg kell adni, hogy mit veszünk egységnyinek. (Pl. 1kg- on a Nemzetközi Súly és Mértékügyi Hivatalban, Sevres-ben őrzött platina-iridium henger tömegét értjük.)

A 7 alapmennyiség a következő:

név jel mértékegység

hosszúság l (s , r , d ) 1 m (méter)

idő t 1 s (másodperc)

tömeg m 1 kg (kilogramm)

anyagmennyiség n 1 mol

hőmérséklet T 1 K (kelvin)

áramerősség I 1 A (amper)

fényerősség I_v 1 cd (kandela)

Származtatott mennyiségek:

Olyan fizikai mennyiségek, melyek más mennyiségek segítségével értelmezhetők.

A származtatott mennyiségek mértékegységei levezethetők az alapmennyiségek mértékegységeiből. Pl. sebesség = út/idő , a sebesség mértékegysége = út mértékegysége/idő mértékegysége = m/s

Kiegészítő mennyiségek:

Melyekről még nem eldöntött, hogy alap, vagy származtatott mennyiségek.

Ezek : a síkszög és a térszög. Jelük valamelyik görög kisbetű ( a b g

A síkszög mértékegységeként a fizikai képletekben mindig a radiánt (rad) használjuk. 1 radián a kör sugarával egyenlő hosszúságú körívhez tartozó középponti szög.

Egy szög radiánban mért értékét egyszerűen meghatározhatjuk a szöghöz tartozó ívhossz és sugár hányadosával. ( pl. a 360 -hoz tartozó körív a kör kerülete , azaz 2rp, így a= 2rp/r = 2p rad )

			a = i / r

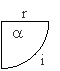
Prefixumok:

Az SI-egységek a gyakorlatban igen sokszor túlságosan kicsinek vagy nagynak bizonyulnak. Ilyenkor az egységeket 10 pozitív vagy negatív egész kitevőjű hatványával szorozzuk és egy a mértékegység elé írt betűvel jelöljük. Pl. cm (centiméter)

A prefixum neve jele szorzótényező

exa E 10¹⁸

peta P 10¹⁵

tera T 10¹²

giga G 10⁹

mega M 10⁶

kilo k 10³

hekto h 10²

deka da 10¹

deci d 10^-1

centi c 10^-2

milli m 10^-3

mikro m 10^-6

nano n 10^-9

piko p 10^-12

femto f 10^-15

atto a 10^-18

kinematika

A fizikának a mozgások időbeli leírásával foglalkozó ága.

Az egyenes vonalú egyenletes mozgás

Egyenes pályán mozgó test egyenlő időközönként egyenlő utakat tesz meg.

s t

v: sebesség

mértékegysége:

( 1 sebességgel 1s alatt 1 m utat tesz meg a test )

Mértékegységként használni szoktuk a is.

(A képletet kivéve csak a használható képletbe történő behelyettesítéskor.)

A sebesség vektor mennyiség. Nagysága mellett iránya is jellemzi.

A sebesség az elmozdulás vektornak és az időnek a hányadosa.

A sebesség relatív mennyiség. Számértéke függ a vonatkoztatási rendszer megválasztásától.

(Ha a feladat nem említi a vonatkoztatási rendszert, akkor értelemszerűen a földhöz viszonyított vonatkoztatási rendszert használunk.)

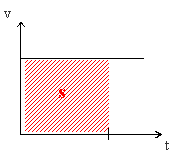
			A sebesség-idő függvény görbe alatti területe megadja az utat. (  a sebesség-idő függvény integráljával adható meg az út.)

Változó mozgások

egyenes vonalú görbe vonalú

a sebesség vektor nagysága változik, iránya nem változik

a sebesség vektor iránya változik, nagysága is változhat

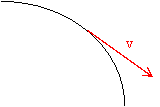Pillanatnyi sebességen azt a sebességet értjük, amivel a test tovább mozogna, ha a mozgásváltozást okozó erőhatás megszűnne. A pillanatnyi sebesség iránya mindig a pálya érintőjének irányába mutat.

Átlagsebesség az a sebesség, amivel a test az adott utat ugyanannyi idő alatt tenné meg, mint a változó mozgással. Jele:   (vagy v_átl. )

Vigyázat! Az átlagsebesség nem egyezik meg a sebességek átlagával!

Egyenes vonalú egyenletesen változó mozgás

A test egyenes vonalú pályán halad és sebessége az idővel egyenes arányban változik, a megtett út pedig az idő négyzetével arányos.

v t                            s t²

Egyszerűbb a mozgás vizsgálata, ha a kezdősebesség nélkül mozog a test.

v₀ = 0

állandó azt jelzi, hogy mennyire gyorsan változik a sebesség, ezért gyorsulásnak nevezzük.

A gyorsulás jele : a 

mértékegysége: : s

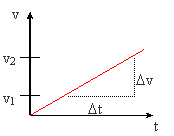
A pillanatnyi sebesség : v = a t képlettel számítható ki.

Az út a sebesség-idő függvény görbe alatti területével meghatározható:

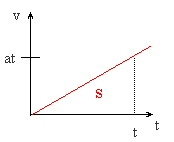
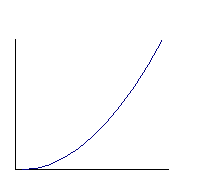
Az egyenes vonalú egyenletesen gyorsuló mozgás út-idő függvénye:

a függvény egy parabola a megtett út az idő négyzetével arányosan változik

t

s

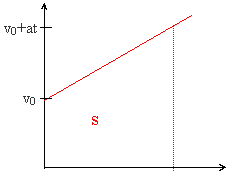
Az egyenes vonalú egyenletesen változó mozgás általános összefüggései

v₀ ¹

v₀ v          Dv = v - v0    

v

képlettel határozható meg a test pillanatnyi sebessége

				Az út a sebesség-idő függvény görbe alatti területével kiszámítható (a pontozással jelölt trapéz területe)      Ez a négyzetes úttörvény.
		t

Lassuló mozgás:

A kezdősebesség nagyobb, mint egy későbbi időpontban a sebesség, ezért a gyorsulás negatív előjelű.

A gyorsulásra, a pillanatnyi sebességre, az útra felírható összefüggések alakja változatlan.

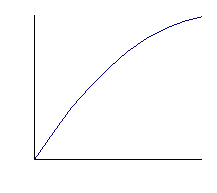
A lassuló mozgás grafikonjai:

Az egyenlő időközönként megtett út egyre kisebb.

t

s

Szabadesés

Testek légüres térben történő esése. ( légüres térben a különböző alakú, tömegű tárgyak egyformán esnek - Galilei)

A szabadesés egyenletesen gyorsuló mozgás.

Gyorsulását nehézségi gyorsulásnak nevezzük (g). Iránya függőlegesen lefelé mutat, értéke függ a földrajzi helytől.

Magyarországon az átlagos értéke: g = 9.81

g értéke a sarkok felé haladva nő, az egyenlítő felé haladva csökken, a tengerszinttől mért távolság nővekedtével csökken. Helyi értékét a közetek sűrűsége kismértékben befolyásolja ( vasérc kőolaj lelőhely felkutatásánál figyelembe veszik - Eötvös féle torziós inga)

A szabadesés matematikai összefüggései:

v₀ = 0

Hajítások

Függőlegesen felfelé

Függőlegesen lefelé

Vízszintes hajítás:

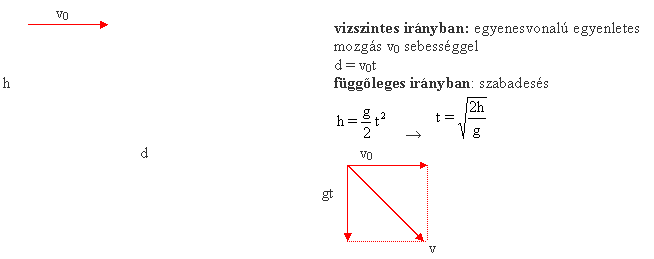
a földetérés sebessége: v (Pitagorasz tétellel számolható)

Ferde hajítás:

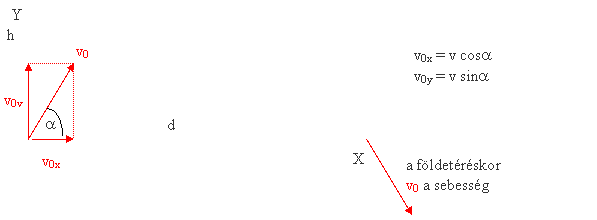
vízszintes irányban (X) : egyenes vonalú egyenletes mozgás v0x sebességgel

d = v_0x t           t = 2t_em (tem: emelkedés ideje = esés ideje)

függőleges irányban (Y): függőleges hajítás felfelé v0y kezdősebességgel

tetőponton: 0 = v_0y -gt_em tem =

h = v_0yt-