A SZIMMETRIA TÖRTÉNETE A FIZIKÁBAN

A SZIMMETRIA TÖRTÉNETE A FIZIKÁBAN

Az előző részben azt állítottuk, hogy az energia, az impulzus és az impulzusnyomaték fogalma teljesen általános és funda­mentális. Ez valóban így van, ezeknél már csak egy lényegesebb fogalom van a természetben, és ez a szimmetria. Ennek megérté­se ugyanolyan alapvető fontosságú, mint az energia fogalmának tisztázása. A szimmetria megértése nélkül ugyanis nem fogjuk megérteni az energia vagy az impulzus fogalmát sem, és így a tiltott találmányok szükségszerű sorsát sem. Látni fogjuk, hogy sorsunk, a tiltott találmányok sorsa és a szimmetriák története milyen szoros, ám láthatatlan kapcsolatban van egymással.

Három területet kell kiemelni a szimmetriákkal kapcsolatban. Először a technikát említem, hiszen ot 838b12i t a gyakorlatban használ­juk ezt a fogalmat, ám a szimmetria megértése, a mély megértése a mai napig is várat magára. Mindig csak véletlenszerűen, ösz­tönszerűen bukkantak rá fontosságára, a szimmetriaműveletek, a szimmetriacsökkentések hasznára. A másik nagy terület a fizika, ahol a szimmetria fogalma szép lassan alakult ki, és a harmadik nagy terület, ahol megintcsak sok-sok buktatóval, várakozással, de a lehető legtisztábban alakult ki ez a matematika. Először a fizikával fogjuk kezdeni, de ott is csak vázlatosan rajzoljuk föl kialakulását. Ezután kicsit részletesebben a matematikában foly­tatjuk a történet elmesélését, hogy utána a technikában és annak szükségszerű gazdasági, politikai vonatkozásaival együtt megis­merjük a szimmetria történetét és hatásait.

A szimmetria is egy általánosan használt és elkoptatott szó ugyanúgy, mint a szeretet és a szocializmus, emiatt szinte min­denki mást ért alatta. Herman Weyl matematikus, a szimmetria egyik kutatója írja a következőket: "A szimmetria tágabb vagy szűkebb értelemben, attól függően, hogy hogyan határozzuk meg e fogalom jelentését az az eszme, melynek segítségével az em­ber az évszázadok során a rendet, a szépséget, a tökéletességet próbálta megérteni és megvalósítani. A fizikában és a techniká­ban a szimmetria a renddel kapcsolatos, a szépség a művészek­nek maradt. Valahogy úgy érezzük, hogy egy egyenesnek, egy körnek, egy csavarnak van bizonyos szimmetriája, ismétlődése, alakzata, rendje: Nem véletlen, hogy a szimmetria fogalma tuda­tosan a fizikában és elsősorban a kristálytanban, az ásványok rendszerezésénél alakult ki, hiszen sokféle kristályráccsal talál­kozunk a természetben.

Itt a szimmetrián azt értjük, hogy ugya­nolyan ismétlődő módon épül fel egy-egy kristály. Egy kocka alakú konyhasó kristály apró darabokra őrölhető, és e piciny ré­szecskékben is megtaláljuk a kocka általunk jól ismert szimmet­riáit. A szabályszerű ismétlődés az, ami itt a szimmetria lé­nyegét jelenti.

A kristálytannak az volt a feladata, hogy felku­tassa a kristályokban fellépő fizikai jelenségek szimmetriáját, és kapcsolatot találjon a fizikai jelenség szimmetriája és kristály geometriai szimmetriája között. Kiderült ugyanis, hogy a kristály alakjától, felépítésétől függően jellemző tulajdonságok kapcsol­hatók hozzá. A kristályok szilárdsága, rugalmassága, átlátszósá­ga, elektromos és mágneses tulajdonságaik, optikai tulajdonsá­gaik, mind felépítésüktől függenek, azaz alapvetően nemcsak a kristályt felépítő anyagtól, hanem a kristályrács szerkezetétől, térbeli szimmetriájától. Ugyanaz az anyag, például a vas, lehet mágneses egyfajta kristályrácsban, és másik kristályrácsban nem mágneses.

A szén például egyik alakzatában lehet gyémánt is, amikor rendkívül kemény és áttetsző, egy másik elrendezésben, másik szimmetriában - amikor grafitként ismerjük akkor pu­ha, elektromosan jól vezető és nem átlátszó. A szénatomok ismétlődési rendje, szimmetriája tehát nagyban befolyásolja tu­lajdonságait. Hasonlóan szélsőséges módon befolyásolja a kris­tály alakja például a foszfor tulajdonságait is.

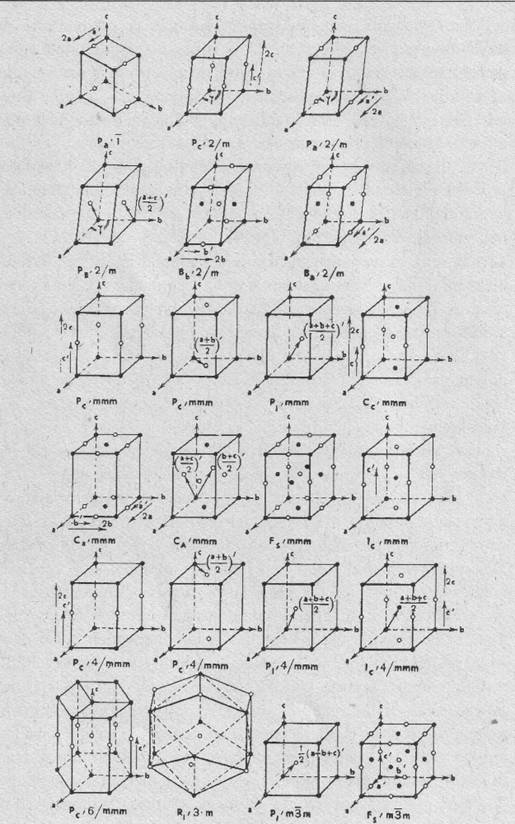
Különböző alakú, eltérő tükrözési és elforgatási tulajdonságokkal, azaz  eltérő szimmetriákkal jellemzett kristályrácsok egy csoportja.

Hogy a kristályok szabályos szerkezetűek, azt a tudományos mondák szerint először a francia René Just Haüy vette észre. Egy papnevelde szerény, félénk tanára, aki a "kristálynyűvő gúnynevet kapta, a legendák szerint a következőképpen bukkant a szabályos felépítés elvére. Egyszer vendégségben egy műkedvelő ásvány­gyűjtőnél kezébe vett egy prizmás, kalcitkristályokból képződött úgynevezett druzát, nézegetni kezdte és véletlenül elejtette. Az összetört és a kristály több hasonló darabra esett szét. Hazatérve Haüy széthasította a gyűjteményében található valamennyi kalcit­kristályt. Noha ezek a legkülönfélébb formájúak voltak, és néme­lyiken a legkevésbé sem lehetett a romboéder lapjait fölfedezni, a hasadványokon csakis ilyen lapokat figyelt meg. A hasadványok aztán mind kisebb és kisebb romboéderekre estek szét. Ennek lát­tán állítólag így kiáltott fel Haüy: "Mindent megtaláltam! : Egy újabb heuréka és egy újabb lépés a szimmetria fogalmának megér­tése felé.

A szerencse, a véletlen és a tapasztalat együttesen így kezdte kialakítani a kristályfizika fogalmait, s vele együtt a szim­metria fogalmait is. Ma már pontosan tudjuk, hogy egy síkban hány­féle szabályosan ismétlődő alakzat képzelhető el, és hogy a térben is (három dimenzióban) véges a szabályosan ismétlődő rácsos alak­zatok száma. Ma egy alakzat szimmetriáján azt a tulajdonságát ért­jük, hogy részei valamely törvény szerint önmagán belül ismétlőd­nek. Ha például egy kockát az ellentétes lapok középpontját össze­kötő négy egyenes bármelyike körül elforgatunk, az minden 90°-os fordulat után önmagát megismétli. Vagy vegyünk egy kevésbé sza­bályos alakzatot, a tégla alakú, derékszögű paralelepipedont.

Ha az élek felezéspontján átmenő síkokkal elvagdaljuk, és a síkok alá eső részeit a felettük levőkkel felcseréljük, azaz tükrözzük, az alakzat önmagába megy át. Ezek a látszólag egyszerű tükrözések és elforgatások alapvetően fontosak voltak a szimmetria fogalmá­nak kialakulásában.

Az történik ugyanis, hogy kiindulunk egy alakzatból, majd transzformáljuk, tehát valamit csinálunk vele, és az eredmény az eredetivel megegyező lesz. Az a jellemző az egyes alakzatokra, hogy a transzformációk, azaz az eltolások, el­forgatások után visszakapjuk az eredeti alakzatot. A kérdés csak az, hogy hány eltolás, hány elforgatás és milyen típusú el­forgatás kell ahhoz, hogy visszakapjuk az eredeti alakzatot. Nem a méret, hanem ezek a transzformációk jellemzik tehát a kristá­lyok és általában az alakzatok szimmetriáit.

Többféle alakú, de azonos szimmetriatulajdonságokat mutató hópelyhek képe. Érdekes kérdés, hogy miért azonos egy-egy hópehely ágainak alakja, honnan "tudhatja az egyik ág, hogy a többin mi történik, milyen alakra kell a jégkristályt növeszteni?

A kezdetekben, amikor még valójában nem tudták, hogyan épül föl az anyag, csak egyfajta homogén közegnek tekintették, észre­vették, hogy a kristály homogén, folytonos és anizotróp közeg, amelynek külső farmáját és tulajdonságait a szimmetria, azaz a ré­szek ismétlődési törvénye határozza meg. A fizikai tulajdonságok és az alakzat, a morfológia szimmetriái közti kapcsolat viszont csak a XIX. század végén, a XX. század elején kapcsolódott össze, akkorra kezdték megérteni a kutatók, hogy az alakzat szimmetriája döntően meghatározza a fizikai tulajdonságokat is. Ez elsősorban Franz Ernst Neumann, Pierre Curie és Valdemar Voight nevéhez fűződik. Az 1930-as években ezt folytatta tovább egy orosz kutató, A. V. Subnyikov, ő emelte igazán tökélyre ezt a tudományterületet.