Budapesti Müszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Automatizálási és Alkalmazott Informatikai Tanszék Alkalmazott Informatika Csoport

T i

Informatika II. gyakorlat

hallgatói segédlet

Fordítók, fordítási technikák

Bevezetés

A mérés célja az elöadás a fordítók, fordítási eljárásokkal kapcsolatban elhangzott információk gyakorlatban történö alkalmazása. Bár ez a segédlet is tartalmaz egy rövid, egyszerüsített összefoglalást erröl a témakörröl, a gyakorlat sikeres elvégzéséhez szükséges az elöadás anyagok ismerete is.

A fordítóprogramok általánosságban képesek egy megadott forrásnyelvek készített adatállományt egy célnyelvre lefordítani. A forrás és a célnyelv sokféle lehet, tipikus példa, hogy egy programozási nyelvröl (C++) gép kódú alkalmazást készítünk, de más lehetöségek is elképzelhetöek, mint ahogy ez a segédlet példáiban is 151g64b látható. A fordítókról rengeteg jó és kevésbé jó leírás van az Interneten[1], ill. nyomtatott könyv formájában.

A föbb fordítási lépések az 1. ábrán láthatóak[3]:

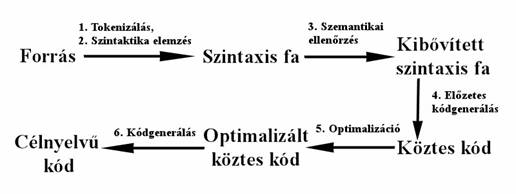
. ábra Fordítási lépések

A kiindulás a forrásnyelvü adatállomány, ami elsö lépésben kisebb blokkokra, tokenekre bontunk. Egy-egy token lehet pl. egy változó, egy szám, vagy karaktersorozat. Ebben a lépésben távolítjuk el a felesleges sortöréseket és szóközöket is. A tokenekböl a következö lépésben a forrásnyelv szabályai szerint szintaxis fát építünk. A szabályok megadása legtöbbször a formális nyelvekben megszokott jelleget követi. A harmadik lépés során a szintaxis fát ellenörizzük szemantikai szempontból, pl. itt végezhetö el a típusok ellenörzése is. A negyedik lépésben a szemantikailag ellenörzött szintaxis fából köztes kódot generálunk. Összetettebb feladatokban ezen a köztes kódon további ellenörzéséket (pl. adatfolyam ellenörzés) végezhetünk el, amivel csökkenthetjük a majdani futásidejü hibák esélyét. Az ötödik lépés során a köztes kódot optimalizáljuk, majd a hatodik lépésben legeneráljuk a célnyelvü adatállományt (pl. bináris kódot).  

A fordítási folyamat elsö két lépése nagyrészt automatizálható, ha a tokenek definícióját és a nyelvtani szabályokat megadjuk. A token-definíciók regurális kifejezések, vagy EBNF leírások segítségével adhatóak meg. A nyelvtani szabályok a formális nyelveknél tanult módon, a mondatszimbólum nemterminálisokra történö bontásával adhatóak meg. Természetesen a nemterminális szimbólumok további felbontását is meg kell adni egészen a terminális szimbólumokhoz vezetö szabályokig.

A mérés során, és a segédletben is az ANTLR[4] nevü programot fogjuk használni a szintaxis fa felépítéséhez. Az ANTLR egy nyelvi definíciós fájl alapján olyan osztályokat generál, amelyek képesek elvégezni a forrás elemzését, tokenekre bontását, valamint a szintaxis fa felépítését. A fa elkészítését követöen a programozó feladata, hogy további ellenörzéseket folytasson (a szemantikai elemzés keretein belül), amennyiben azokra szükség van, ill. kódot generáljon a szintaxis fa alapján.

Az ANTLR által használt definíciós fájlt általában ".g" kiterjesztéssel hozzuk létre. A fájl a következö elemekböl épül fel:

1. Header fájlok inicializálása
2. Nyelvi beállítások
3. A Parser osztály definíciója (nyelvi szabályok)
4. A Lexer osztály definíciója (tokenek)
5. A TreeParser osztály definíciója (osztály a fa feldolgozásához)

Az 1. pontra akkor van szükség, ha saját faépítö algoritmust szeretnénk létrehozni (l. 3. feladat), különben ez a lépés kihagyható.

A 2. pont azt szabályozza, hogy a nyelvi definíciót milyen programozási nyelv (C++, C#, Java, .) szintaktikájával kell értelmezni, ill. milyen nyelvüek legyen a definíciós fájlból generált osztályok. Ez egy nagyon fontos lépés, ugyanis az ANTLR Java alapú program, alapbeállításként Java osztályokat generál, ami a jelen mérésben nem megfelelö, mivel a mérés a fordítók C++ alapú változatát írja elö.

A 3. pont a forrásnyelv definíciója EBNF[5] formában megadott szabályok formájában. Fontos megemlíteni, hogy az egyes szabályok elé és mögé saját kódrészleteket illeszthetünk be, amennyiben az szükséges. Ezek a kódrészletek képesek pl. az aktuális kifejezés értékét tárolni és változtatni a forrásban megadott müveleteknek megfelelöen.

A 4. pont a tokenek definícióját tartalmazza, egyszerü példák a tokenek megadására a z ANTLR honlapján[6] találhatóak.

Az 5. pont elhagyható, amennyiben saját fa reprezentációt alkalmazunk, vagy ha az elkészült szintaxis fán semmilyen müveletet sem szeretnénk elvégezni. A TreeParser-ek segítségével egyszerüen adhatunk meg a fa alapján elvégzendö müveleteket.

Az ANTLR által generált (C++) nyelvü fájlokat egy Visual Studio project fájlba kell foglalni, majd le kell fordítani, aminek eredményeképpen kapunk egy egyszerü, de hatékony nyelvtani elemzöt a kiválasztott forrásnyelvhez.

Az ANTLR telepítése

A https://www.imada.sdu.dk/~morling/issue1.htm honlap részletesen leírja, hogy hogyan lehet az ANTLR programot otthoni környezetben beüzemelni. Habár a leírás egy régebbi ANTLR verzióhoz készült, mint amit a mérésen használni fogunk, a föbb lépések mégis megtalálhatóak a leírásban:

1. Le kell tölteni (és fel kell telepíteni) az ANTLR legújabb verzióját a https://www.antlr.org oldalról
2. Le kell tölteni és fel kell telepíteni a Java Development Kit legújabb verzióját
3. Hozzá kell adni a Path környezeti változóhoz a Java bin könyvtárát (ha az nem került oda magától)
4. Meg kell adni egy ClassPath nevü környezeti változót, itt a honlapon szerelötöl eltéröen elegendö a C:\antlr277\lib\antlr.jar értéket megadni (természetesen az ANTLR telepítési könyvtárát átírva), majd újra kell indítani a gépet (!)
5. Létre kell hozni Visual Studioban egy új, üres solution fájt[7], majd ehhez hozzáadni egy új C++ projectet.
6. Meg kell adni a következöket a project beállításainál:
1. AdditionalIncludeDirectories ="C:\antlr\277\include"
2. AdditionalDependencies  ="C:\antlr\277\lib\antlr.lib"
3. AdditionalLibraryDirectories ="C:\antlr\277\lib"
7. A projecthez hozzá kell adni az egyes feladatok .g fájljából generált .cpp és .hpp fájlokot, majd le kell fordítani. A .g .cpp átalakítás parancssorból a java antlr.Tool mydeffile.g parancsot kell kiadni, ahol a mydeffile.g tartalmazza a forrás nyelvének definícióját.

A mérésre való felkészülést segítendö jelen segédlet mellé letölthetök a project fájlok is, amikben csak az ANTLR telepítési útvonalát kell átírni (amennyiben az szükséges).

I. Példa - Egyszerüsített számológép

Az elsö feladat egy, a standard inputon megadott müveletsor beolvasása és a müvelet eredményének kiírása. A müveletsor csak egész számokat ill. a "+" és a "*" müveletet tartalmazhatja.

A feladat megoldása a  .g fájl megadásával történik

//Meg kell adni, hogy C++ nyelvü osztályokat szeretnénk generálni

options

// A parser osztály tesreszabása

class CalcParser extends Parser;

options

// A nyelvtani szabályok, ahol expr a teljes kifejezés (a

// mondatszimbolum). Ez a szabaly azt irja le, hogy egy kifejezes

// az mexpr és a PLUS nevü szimbolumok sorozatából adódnak ki. A

// kifejezést pontosvesszovel zarjuk le.

expr  : mexpr (PLUS^ mexpr)* SEMI!

;

// Az mexpr szimbolum felbontasanak szabalya, ami

// kimondja, hogy az atom es a STAR szimbolumok sorozatara bonthato

mexpr : atom (STAR^ atom)*

;

// Az atom tovabb bonthato pontosan egy INT-re

atom: INT;

// A lexer (a tokeneket analizalo) osztaly definicioja

class CalcLexer extends Lexer;

// A "white space" karaktereket (pl. sor vege) ki kell hagyni, azok

// nem kepeznek kulon tokent

WS_   : (' ' | '\t' | '\n' | '\r')

;

// Az egyszeru tokenek definicioja

STAR: '*';

PLUS: '+';

SEMI: ';';

// Egy INT szam szamjegyek sorozatabol epul fel

protected

DIGIT: '0'..'9';

INT : (DIGIT)+;

// Az alapertelmezett fabejaro osztalyt szeretnenk hasznalni

class CalcTreeWalker extends TreeParser;

// szamitsuk ki a forras, azaz a bemeneti muveleti sor eredmenyet

expr returns [float r]

: #(PLUS a=expr b=expr)

| #(STAR a=expr b=expr)

| i:INT

;

A .g fájlból a korábban leírt módon generálhatjuk le a C++ osztályokat. Ezeket a fájlokat adjuk a projecthez.

A következö lépés a statikus Main függvény definiálása.

#include <iostream>

#include <sstream>

// Az ANTLR osztalyara is szukseg van a fa epitesehez

#include "antlr/AST.hpp"

// A generalt fajlok

#include "CalcLexer.hpp"

#include "CalcParser.hpp"

#include "CalcTreeWalker.hpp"

int main( int argc, char* argv[] )

input_string.str(expr.str());

input = &input_string;

filename = "<arguments>";

}

// A lexer inicializalasa

CalcLexer lexer(*input);

lexer.setFilename(filename);

// A parser inicializalasa (szuksege van a lexerre!)

CalcParser parser(lexer);

parser.setFilename(filename);

//A faepito rutinok inicializalasa

ASTFactory ast_factory;

parser.initializeASTFactory(ast_factory);

parser.setASTFactory(&ast_factory);

//A forra tenyleges feldolgozasanak megkezdese

parser.expr();

// A szintaxis fa kinyerese a parser-tol

RefAST t = parser.getAST();

// Sikerult a fa felepitese?

if( t )

else

}

catch(ANTLRException& e)

catch(exception& e)

return 0;

A project fájlt (megtalálható mellékletként) ezek után már csak fordítani és futtatni kell. A program a standard inputról olvassa be a kifejezést, amit ki kell számolnia.

II. Példa - Számológép vektormüveletekhez

A második feladat egy, a standard inputon megadott müveletsor beolvasása és a müvelet eredményének kiírása. A müveletsor vektorokat, összeadást ("+"), szorzást ("*") ill. zárójeleket tartalmazhat.

Ez a feladat annyival bonyolultabb az elözönél, hogy itt a skalárok helyett vektorokkal végezzük el a müveleteket. Ez az egyszerünek tünö változtatás jelentösebb módosításokat igényel:

Az elsö feladatban az ANTLR által felkínált fa szerkezetet használtuk fel, ami egyrészröl kényelmes volt, hiszen a fa csomópontjainak építése nagyrészt automatizálható volt, másrészröl viszont ez az ábrázolás tartalmaz néhány megkötést, ami megnehezítheti a fa feldolgozását. Ennélfogva a példában egy új fa típust fogunk használni. Ez a fa a Tree osztályban található meg, ami tartalmazza az alapvetö faépítö és kiírató függvényeket, valamint a fa csomópontjainak (vektorok és müveleti jelek) kezelését. A Tree osztályban az egyes csomópont típusokhoz egy-egy egész számot rendelünk, ami a csomópont típusának a kódját reprezentálja. Ezeknek a kódoknak a feloldása a NodeTypes.hpp fájlban találhatóak meg.

A vektorok kezeléséröl, a vektorok összeadásának és szorzásának elvégzéséröl szintén gondoskodni kell. Erre szolgál a Vector template osztály, ahol a template típusának jelen esetben "int"-et használunk majd. Ez az osztály nem függ a fordítótól, a fa felépítésétöl, hanem valóban csupán az alapvetö vektormüveleteket tartalmazza.

Mivel a feladat megoldásához szükséges kiegészítö osztályok megvannak[8] így a következö lépés a nyelvi definíciós fájl megváltoztatása:

Meg kell adni, hogy nem a beépített fa építö algoritmust szeretnénk használni:

header "post_include_hpp"

class CalcParser extends Parser;

options

A nyelvtan szabályai is más felépítésüek lesznek, pl.

expr returns [Tree* pt1]

: pl1=mexpr

(PLUS^ pr1=mexpr )*

else

;

Ez a szabály egyrészt kifejezi azt, hogy az expr tovább bontható egy mexpr szimbólumra és egy pluszjel - mexpr párosból adódott sorozatra. Másrészt viszont a szabály tartalmaz kódrészleteket is, amik a fa építését végzö müveletek hívásáról gondoskodnak. A nyelvtani szabályok így bonyolultabb felépítésüek lesznek, de a bövítés révén a müveletek szélesebb skáláját lehet rajtuk elvégezni.

A zárójelek ill. a vektorok feldolgozásához új szabályokra (nyelvi is token-jellegü) is szükség van. Ezek a szabályok a korábbiakhoz hasonlóan a formális nyelveknél megszokott módon adhatóak meg.

mexpr returns [Tree* pt2]

: pl2=element

(STAR^ pr2=element )*

else

;

element returns [Tree* pt3]

: pm3=vector

| LPAREN! pm3=expr RPAREN!

;

vector returns [Tree* pt4]

: LBRACKET! pl4=atom

(SEMI pr4=atom )* RBRACKET!

;

LPAREN: '(';

RPAREN: ')';

LBRACKET: '[';

RBRACKET: ']';

COMMA:  ',';

A vektorok összeadása és szorzása csak akkor értelmezhetö, ha a vektorok nagysága megegyezik. Ezt az információt a szemantikus elemzés során ellenörizhetjük. A szemantikus elemzés ebben az esetben végignézi a korábban elkészített szintaxis fát és megnézi, hogy a müveletekben rész vevö vektorok mérete megfelelö-e. Ez a logika a SemanticAnalyser.cpp fájlban található. A pluszjel esetében pl. kiolvassuk az aktuális csomópont két gyermek elemét (a müvelet két operandusát), a fa csomópontokból rekurzív módon vektorokat készítünk, majd összehasonlítjuk azok sorainak számát. A szorzásnál hasonló módszerrel ellenörizzük, hogy az adatok szemantikai szempontból megfelelöek-e.

Az utolsó teendönk a Main függvény átírása, ami viszonylag egyszerüen elvégezhetö:

.

CalcParser parser(lexer);

parser.setFilename(filename);

Tree* pt = parser.sentence();

if( pt )

catch (char* s)

}

III. Példa - Számológép HTML kimenettel

A harmadik példafeladat a korábbiakban elkészült vektorokat kezelö számológép kiegészítése olyan módon, hogy az képes legyen az eredményt és az operandusokat HTML formátumban megjeleníteni.

A harmadik példa a korábban elkészített számológép kibövítése, hogy az HTML kimenetet adjon, azaz mintegy kódot generálunk a forrás adatállományból. A feladathoz nagy segítséget nyújt a HtmlGenerator osztály, ami a szemantikus analízishez hasonlóan képes a szintaxis fán rekurzívan navigálva az egyes csomópontokhoz HTML nyelvü kódot generálni. Az osztály felépítése meglehetösen egyszerü, általánosnak mondható. A GetHTML függvény legenerálja a HTML vázát, míg a GetHTMLRecursive függvény elvégzi a paraméterként megkapott szintaxis fához (vagy fa részlethez) tartozó kód generálását. Az egyes müveletekböl egymásba ágyazott táblázatokat készít. A vektor osztály képes önmagát HTML formátumban megjeleníteni a toHtml függvény segítségével.

A példa az elsö két példához képest egyszerü ugyan, de leegyszerüsített formában megmutatja a kódgenerálás egyik lehetséges módszerét.