A stacionárius elektromos áram törvényei

1. Az áramsûrûség forrásbõsége

Tekintsük, hogy a vezetõben egyenáram folyik (tehát és ) és szemléltesse a 3.2 ábra a vezetõ egy olyan darabját, ahol a vezetõ keresztmetszete változó méterû.

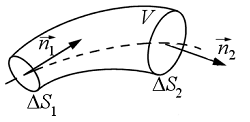
3.2 ábra

Stacionárius áramlás esetében a vezetõ bármely keresztmetszetén egységnyi idõ átfolyó töltéshordozók száma azonos kell legyen. Ellenkezõ esetben töltéshordozók kellene keletkezzenek vagy eltûnjenek ami viszont nem lehetséges. Tekintsük, hogy 323h71d egységnyi idõ alatt a felületen töltés lép be a zárt térfogatba és a felületen lép ki. A fenti kijelentésnek megfelelõen . Ahhoz, hogy megkapjuk a 3.2 ábrán feltüntetett véges és felületeken áthaladó töltéshordozók számát, összegeznünk minden a fentiekben leírt elemi felület hozzájárulását, ami matematikailag integrálok felírását jelenti. Felhasználva a (3.5) összefüggést írhatjuk, hogy:

amely tulajdonképpen nem más, mint az áramsûrûség vektornak a két érintett felületre vonatkoztatott fluxusai közötti egyenlõség. Mivel a vezetõ oldalfalain keresztül nincs töltéshordozó mozgás, a (3.6) összefüggést írhatjuk a térfogatot körülzáró zárt felületre. Ilyen formán azt kapjuk, hogy az áramsûrûség vektornak a zárt felületre vonatkoztatott fluxusa nulla (3.7).

Felhasználva a vektoranalízisbõl ismert Gauss-Osztrogradszkij-integrálegyenletet, a fenti felületi integrált átalakíthatjuk egy a zárt felület által határolt térfogaton vett integrálra:

Az itt megjelenõ mennyiség nem más, mint a divergenciája (forrásbõsége). Mivel a kifejezés nullával egyenlõ, ez csak úgy lehetséges, ha maga az integrálandó mennyiség értéke egyezik meg nullával, így a divergenciája nulla.

Ez azt jelenti, hogy az áramsûrûség vektortérnek nincs forrása, vagyis az áramsûrûség vektorterének erõvonalai zártak.

2. A kontinuitási egyenlet

Az 1.3.1. ponthoz hasonló elrendezést tekintünk a továbbiakban is, azonban feltételezzük, hogy az áramerõsség idõben nem állandó, tehát , tehát a teljes felületre számított fluxus idõben változó lehet, de nullától különbözõ valamint a felületen belépõ töltésmennyiség nem egyenlõ a töltésmennyiséggel (3.2 ábra). Ennek természetes következménye, hogy a tekintett térfogatban a töltések száma idõben meg kell változzon, amit egy mennyiséggel veszünk figyelembe. Két lehetséges folyamatot kell megvizsgáljunk ahhoz, hogy a fentieknek pontos matematikai kifejezést adjunk. Amennyiben az áram erõssége csökken, a teljes felületre számított fluxus pozitív, de csökken a térfogatban lévõ töltéshordozók száma, amennyiben pedig az áramerõsség nõ, a teljes fluxus negatív, viszont megnõ a térfogatban lévõ töltéshordozók száma. Ennek megfelelõen a teljes fluxus minden esetben a töltés idõbeli változásának negatív értékével kell egyenlõ legyen (3.10)-nek megfelelõen.

Ezt az összefüggést nevezzük kontinuitási egyenletnek, amely magába foglalja a töltésmegmaradás elvét is.

3. Az stacionárius áram elektromos terére vonatkozó megállapítások

a)      Az elektromos tér forrásbõsége.

Tekintsük kiindulási pontnak az elektrosztatikában megismert Gauss törvényt, mely kimondja, hogy az elektromos térerõsség vektorának zárt felületre vonatkoztatott fluxusa arányos a zárt felület által határolt térfogatban lévõ eredõ töltésmennyiséggel és a következõképpen fejezhetõ ki:

A stacionárius elektromos áramot a töltéshordozókra ható elektromos tér tartja fent. Alkalmazzuk a Gauss-törvényt tehát a stacionárius elektromos áram esetére. Ehhez a (3.11) összefüggés jobb oldalát kell megvizsgáljuk. Egy zárt felület által határolt térfogatot kell tekintsünk, amelybe töltéshordozók érkeznek, de ugyanakkor távoznak is. Mivel a töltéshordozók áramlása stacionárius a beérkezõ és a távozó töltéshordozók száma azonos kell legyen. A Gauss-törvény alkalmazásánál azonban figyelembe kell vennünk egy elõjelszabály is, nevezetesen azt, hogy minden belépõ töltés negatív elõjellel és minden kilépõ töltés pozitív elõjellel kell szerepeljen. Ha ezt figyelembe vesszük, a Gauss-törvényt a következõ alakban kell felírjuk:

ahol , tehát

Alkalmazzuk (3.13)-ra Gauss-Osztrogradszkij-integrálegyenletet és kapjuk, hogy

melybõl következik, hogy a stacionárius áram elektromos terének divergenciája nulla, tehát az elektromos tere forrásmentes:

Ez a törvény a stacionárius áramra vonatkozó I. Maxwell-törvény.

b)      Az elektromos tér örvényessége.

Tapasztalati tény (ismert az elektrosztatikából), hogy ha egy töltés stacionárius elektromos térben zárt görbe mentén mozog, az elektromos térnek a töltésen végzett munkája nulla, vagyis:

Mivel a töltés nullától különbözõ, a fenti összefüggésbõl következik, hogy az elektromos tér zárt görbére számított cirkulációja nulla:

Alkalmazzuk (3.17)-re a Stokes-integrálegyenletet:

tehát az elektromos tér örvénymentes, vagyis konzervatív.

Ez a törvény a stacionárius áramra vonatkozó II. Maxwell-törvény. A stacionárius elektromos tér örvénymentességébõl következik többek között az is, hogy minden pontot jellemezhetünk egy adott potenciállal és a pontok között potenciálkülönbség, vagy más néven feszültség van (pl. a és pontok között feszültség van, míg ha az elektromos tér egy töltést az A-tól B pontba szállít, rajta munkát végez.