|
|
||
|
|||||||||||||||||||
Előző tanulmányokból a komplex számok és a velük kapcsolatos alapvető műveletek már ismertek, azonban a könnyebb eligazodás kedvéért ezen bevezető részben összefoglaljuk ezeket. A 13. ábrán a komplex számsík látható.
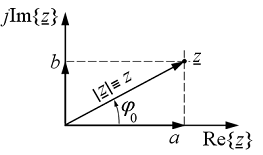
13. ábra
Egy komplex szám megadható a (4.22) összefüggésekkel:
|
|
|
ahol, ![]() ,
, ![]() a komplex szám valós
része,
a komplex szám valós
része, ![]() a komplex szám
képzetes (imaginárius) része,
a komplex szám
képzetes (imaginárius) része, ![]() a komplex szám
modulusza és
a komplex szám
modulusza és ![]() a fázisa. A fázis
(fázisszög), előjellel rendelkező mennyiség, vonatkoztatása a pozitív valós
tengelyhez történi, irányítása megegyezik a trigonometriai iránnyal (a 13. ábrán
látható
a fázisa. A fázis
(fázisszög), előjellel rendelkező mennyiség, vonatkoztatása a pozitív valós
tengelyhez történi, irányítása megegyezik a trigonometriai iránnyal (a 13. ábrán
látható ![]() fázis pozitív). A (4.22)
összefüggés jobb oldalát az Euler-képlettel kifejthetjük és kapjuk a következő
összefüggést,
fázis pozitív). A (4.22)
összefüggés jobb oldalát az Euler-képlettel kifejthetjük és kapjuk a következő
összefüggést,
|
|
|
tehát a komplex
szám valós része (![]() ) és az imaginárius része (
) és az imaginárius része (![]() ) is megadható a modulusza és a fázisa függvényében.
) is megadható a modulusza és a fázisa függvényében.
Az alábbiakban felsorolunk néhány tulajdonságot és műveletet:
- a komplex szám konjugáltja: ![]() ,
,
- komplex számok összeadása: ![]() ,
,
- komplex számok kivonása: ![]() ,
,
- komplex számok szorzása: ![]() ,
,
- komplex szám négyzete: a komplex számnak
saját konjugáltjával való szorzását jelenti: ![]() ,
,
- komplex számok osztása: komplex szám 727c25h ok osztásánál a számlálót és a nevezőt is szorozzuk a nevező komplex konjugáltjával és addig alakítjuk az összefüggést, amíg megfelelő alakra hozzuk:
![]()
![]() .
.
A komplex számok használata nagyon előnyös a váltakozó áram és a váltakozó áramú áramkörök tárgyalásnál, mivel a komplex számokkal nagyon könnyen lehet kezelni az olyan mennyiségeket, amelyek nincsenek fázisban egymással.
Amint azt az 1.6. pontban már
bemutattuk, a váltakozó áramot/feszültséget időben szinusz vagy koszinusz
függvénnyel írhatjuk le. A két függvény között mindössze ![]() -es fáziskülönbség van. A komplex tárgyalásmód formális
jellegű, természetesen az áramkörökben nem keringnek komplex áramok és az
áramköri elemek sarkain nem komplex feszültségek jelennek, meg, azonban
formálisan áttérhetünk ilyen mennyiségekre, amelyek számításainkat
megkönnyítik, majd a kívánt eredmény elérése után visszatérünk a valós időbeli
lírásra. Tekintsünk egy az 1.6.1. pontban lévő lírásnál használt szinuszos
pillanatnyi értékkel rendelkező feszültséget,
-es fáziskülönbség van. A komplex tárgyalásmód formális
jellegű, természetesen az áramkörökben nem keringnek komplex áramok és az
áramköri elemek sarkain nem komplex feszültségek jelennek, meg, azonban
formálisan áttérhetünk ilyen mennyiségekre, amelyek számításainkat
megkönnyítik, majd a kívánt eredmény elérése után visszatérünk a valós időbeli
lírásra. Tekintsünk egy az 1.6.1. pontban lévő lírásnál használt szinuszos
pillanatnyi értékkel rendelkező feszültséget, ![]() . Definíció szerint a komplex pillanatnyi feszültséget a
következő összefüggéssel határozzuk meg:
. Definíció szerint a komplex pillanatnyi feszültséget a
következő összefüggéssel határozzuk meg: ![]() . Ebből az összefüggésből a visszatérést a valós időbeli
leíráshoz a következő (Euler-képletre alapuló) összefüggés biztosítja:
. Ebből az összefüggésből a visszatérést a valós időbeli
leíráshoz a következő (Euler-képletre alapuló) összefüggés biztosítja:
![]()
Hasonlóképpen
definiálhatjuk az áramkörben folyó komplex áramot is. Legyen az áram
pillanatnyi értéke ![]() (általában nincs
fázisban a feszültséggel), tehát a komplex pillanatnyi érték
(általában nincs
fázisban a feszültséggel), tehát a komplex pillanatnyi érték 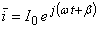 .
.
A
fentiekben definiált komplex mennyiségeknél néhány pontosítást kell tennünk. A
komplex pillanatnyi értékek felírhatók egy időtől független tag, melyet komplex
amplitúdónak nevezünk, és egy időtől függő tag szorzataként. Pl. a pillanatnyi
komplex feszültség: ![]() . Itt az
. Itt az ![]() mennyiség a komplex
amplitúdó, melyet az
mennyiség a komplex
amplitúdó, melyet az ![]() összefüggés definiál.
összefüggés definiál.
A komplex mennyiségeket gyűjtőnéven
fazoroknak nevezzük és 13. ábrának megfelelően a komplex számsíkban ábrázoljuk.
Példaként ábrázoljuk a fentiekben bevezetett komplex pillanatnyi feszültséget
és áramot, feltételezve, hogy feszültség siet az áramhoz képest, tehát ![]() .
.
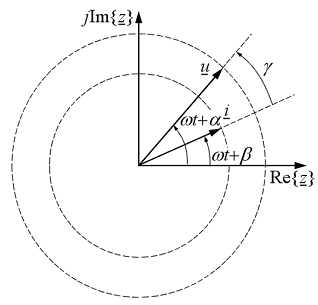
14. ábra
A 14. ábrának megfelelően a komplex
pillanatnyi feszültség és áram olyan fazorok, amelyek a ![]() szögsebességgel
forognak és egymáshoz képest a fáziskülönbségük állandó,
szögsebességgel
forognak és egymáshoz képest a fáziskülönbségük állandó, ![]() értékkel rendelkezik. Ugyanígy
ábrázolhatjuk a komplex amplitúdókat is, melyek a komplex számsíkban állandó
helyzetben vannak. Természetesen a valós mennyiségekhez hasonlóan a komplex
mennyiségeknél is definiálhatjuk az effektív értékeket. Pl. a feszültség
komplex effektív értéke
értékkel rendelkezik. Ugyanígy
ábrázolhatjuk a komplex amplitúdókat is, melyek a komplex számsíkban állandó
helyzetben vannak. Természetesen a valós mennyiségekhez hasonlóan a komplex
mennyiségeknél is definiálhatjuk az effektív értékeket. Pl. a feszültség
komplex effektív értéke ![]() .
.
A komplex alakban felírt feszültség és áram között az eddigiekben már megismert Ohm-törvény a továbbiakban is érvényes marad. A feszültség és az áram aránya megadja az illető áramköri elem komplex látszólagos ellenállását, más néven impedanciáját, melyet a (4.24) összefüggéssel definiálunk.
|
|
|
ahol, ![]() a valós impedancia és
a valós impedancia és ![]() az impedancia
fázisszög.
az impedancia
fázisszög.
A (4.24) összefüggésben látszik, hogy a komplex impedancia magába foglalja az áramköri elem látszólagos ellenállást (impedanciáját) és a feszültség és az áram között kialakuló fáziseltolást is. Ahhoz, hogy egy összetett váltakozó áramú áramkört tanulmányozhassunk, elsődlegesen szükségünk van az egyszerű váltakozó áramú ellenállások komplex ellenállásainak ismeretére. A továbbiakban ezeket határozzuk meg, figyelembe véve a 2.3. pontban leírt ismereteket. A (4.24) összefüggést átírhatjuk a következő alakba is:
|
|
|
ahol, ![]() a hatásos ellenállás
és
a hatásos ellenállás
és ![]() a reaktív ellenállás
(reaktancia),
a reaktív ellenállás
(reaktancia), ![]() és
és ![]() .
.
a.) Ellenállás
Megállapítottuk, hogy az ohmos
ellenállás nem okoz fáziskülönbséget a feszültség és az áram között, így a (4.24)
összefüggésben lévő fáziseltolás értéke ellenállás esetére ![]() , tehát,
, tehát,
|
|
|
ami azt jelenti, hogy az ellenállás komplex impedanciája nem más, mint a valós ellenállása.
b.) Tekercs
Megállapítottuk, hogy egy ideális
tekercsen a feszültség ![]() -vel siet fázisban az áramhoz képest, így a (4.24)
összefüggésben lévő fáziseltolás értéke
-vel siet fázisban az áramhoz képest, így a (4.24)
összefüggésben lévő fáziseltolás értéke ![]() , tehát,
, tehát,
|
|
|
c.) Kondenzátor
Megállapítottuk,
hogy egy ideális tekercsen a feszültség ![]() -vel késik fázisban az áramhoz képest, így a (4.24)
összefüggésben lévő fáziseltolás értéke
-vel késik fázisban az áramhoz képest, így a (4.24)
összefüggésben lévő fáziseltolás értéke ![]() , tehát,
, tehát,
|
|
|
A komplex impedancia fordított értékét komplex admittanciának nevezzük és a (4.29) összefüggéssel definiáljuk,
|
|
|
ahol, ![]() a valós admittancia és
a valós admittancia és
![]() az admittancia fázisszög,
az admittancia fázisszög,
![]() a valós vezetés
(konduktancia) és
a valós vezetés
(konduktancia) és ![]() a látszólagos vezetés
(szuszceptancia),
a látszólagos vezetés
(szuszceptancia), ![]() és
és ![]() .
.
a.) Ellenállás
A (4.29) összefüggésben az
ellenállás admittancia fáziskülönbség ![]() , tehát
, tehát
|
|
|
ami azt jelenti, hogy az ellenállás komplex admittanciája nem más, mint a vezetőképessége.
b.) Tekercs
Tekercs esetében az admittancia
fáziskülönbség ![]() , így (4.29)-ból a tekercs komplex admittanciája,
, így (4.29)-ból a tekercs komplex admittanciája,
|
|
|
c.) Kondenzátor
Kondenzátor esetében az admittancia
fáziskülönbség ![]() , így (4.29)-ból a kondenzátor komplex admittanciája,
, így (4.29)-ból a kondenzátor komplex admittanciája,
|
|
|
Az előző pontokban azt láttuk, hogy miként alkalmazzuk az Ohm-törvényt a váltakozó áramú ellenállásokra. Az összetett áramköröket a váltakozó áramú ellenállások és a váltakozó áramú áramforrások különböző kapcsolásaival állítjuk össze. Átírva a mennyiségeket komplex alakba, ugyanúgy alkalmazhatjuk a Kirchhoff-törvényeket, mint az egyenáramú áramkörök esetében. A különbség talán csak annyi, hogy a váltakozó áramú áramkörökben a Kirchhoff-törvényeket felírhatjuk a mennyiségek komplex pillanatnyi értékeire, amplitúdóira vagy effektív értékeire is.
- Ohm-törvény:
|
|
|
- I. Kirchhoff-törvény:
|
|
|
- II. Kirchhoff-törvény:
|
|
|
Hasonlóan az egyenáramú áramkörökhöz, a váltakozó áramú ellenállásokra is érvényesek a már megismert kapcsolási szabályok:
- soros kapcsolás:
|
|
|
- párhuzamos kapcsolás:
|
|
|
Megjegyezzük, hogy a csillag-delta illetve delta-csillag átalakítások az egyenáramú áramköröknél leírt módon, komplex mennyiséggel alkalmazhatók.
A váltakozó áramú áramkörök megoldásához ugyanazokat a módszereket alkalmazhatjuk, amelyeket az egyenáramú áramköröknél már megismertünk (Kirchhoff-törvények, szuperpozíció elv, Thèvenin-tétel, Norton-tétel stb.). A különbség az egyenletekben szereplő mennyiségek megfelelő felírásában jelentkezik, mivel minden mennyiséget át kell írni komplex alakba, majd alkalmazunk valamilyen módszert az áramkör megoldására, majd a kapott komplex eredményeket vissza kell írjuk időben szinuszosan vagy koszinuszosan változó alakba.
Megjegyzés: minden ellenállás, amely az egyenáramú áramköröknél szerepelt a különböző egyenletekben, a váltóáramú áramköröknél a megfelelő impedanciákkal helyettesítendő!
Tekintsük a 15. ábrán látható soros RLC áramkört, amelyben egy ![]() pillanatnyi értékkel
rendelkező váltakozó áramú áramforrás található. Ennek hatására az áramkörben
pillanatnyi értékkel
rendelkező váltakozó áramú áramforrás található. Ennek hatására az áramkörben ![]() pillanatnyi erősségű
áram folyik. Ahhoz, hogy ezt az áramot a komplex számok módszerével
meghatározhassuk, először meg kell határozzuk a feszültség komplex pillanatnyi
értékét:
pillanatnyi erősségű
áram folyik. Ahhoz, hogy ezt az áramot a komplex számok módszerével
meghatározhassuk, először meg kell határozzuk a feszültség komplex pillanatnyi
értékét: ![]() . Innen meghatározhatjuk a komplex effektív értéket:
. Innen meghatározhatjuk a komplex effektív értéket: ![]() . A továbbiakban használhatjuk az áramkör megoldásához a
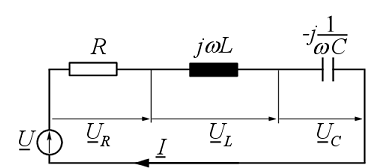
komplex pillanatnyi vagy effektív értéket, vagy a komplex amplitúdót is. A 16. ábrán
a komplex effektív értéket tüntettük fel.
. A továbbiakban használhatjuk az áramkör megoldásához a
komplex pillanatnyi vagy effektív értéket, vagy a komplex amplitúdót is. A 16. ábrán
a komplex effektív értéket tüntettük fel.
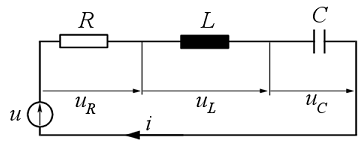
15. ábra
16. ábra
Ezek után a váltakozó áramú ellenállásokat kell átírni komplex alakba, melyet a 16. ábrán tüntettünk fel. Az áramkörre a huroktörvényt a komplex mennyiségekkel a következő alakban írhatjuk fel:
|
ahol
tehát
és az áramkörben folyó áram erőssége
|
|
A (4.38) összefüggésben szereplő
komplex impedanciát (![]() ) felírhattuk volna a komplex ellenállások soros
kapcsolásából származó eredő impedancia segítségével is:
) felírhattuk volna a komplex ellenállások soros
kapcsolásából származó eredő impedancia segítségével is:
|
|
|
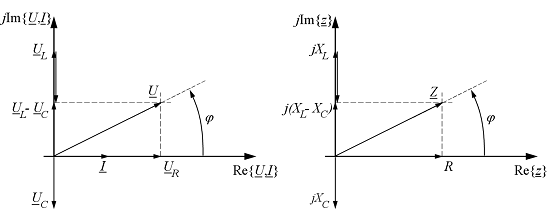
Figyelembe véve a 2.2. pont fáziseltolásokra vonatkozó eredményeit, illetve a komplex számoknak komplex számsíkban való ábrázolására vonatkozó szabályokat, megrajzolhatjuk a soros RLC áramkör fazorábráit (17.a-b ábrák).
Megjegyzés: Az ábrázolt esetben azt feltételeztük, hogy az áramkör induktív jellegű, ami azt jelenti, hogy a feszültség siet az áramhoz képest. Ha a tekercsen lévő feszültség abszolút értéke kisebb, mint a kondenzátoron megjelenő feszültség, az áramkör kapacitív és a feszültség késik az áramhoz képest, a fázisszög negatív. Ha viszont a két feszültség abszolút értékei egyenlők, a fázisszög nulla és az áram fázisban van a feszültséggel. Ezt az állapotot rezonanciának nevezzük (soros RLC áramkörben egészen pontosan feszültségrezonanciának).
Az
17.a ábrán az áramköri elemeken megjelenő feszültségeket, illetve az áramot
tüntettük fel, figyelembe véve, hogy az ellenálláson nincs fáziskülönbség, a
tekercsen siet ![]() -vel a feszültség az áramhoz képest (komplex alakban ez
-vel a feszültség az áramhoz képest (komplex alakban ez ![]() -vel való szorzást jelent), míg a kondenzátoron késik
-vel való szorzást jelent), míg a kondenzátoron késik ![]() -vel a feszültség az áramhoz képest (komplex alakban ez
-vel a feszültség az áramhoz képest (komplex alakban ez ![]() -vel való szorzást jelent). Ugyanezt végeztük el a 17.a ábrán
a komplex impedanciákkal.
-vel való szorzást jelent). Ugyanezt végeztük el a 17.a ábrán
a komplex impedanciákkal.
a. b.
17. ábra
Elvégezve
a műveleteket a komplex számokkal, az a. esetben megkapjuk az áramforrás
sarkain lévő feszültség komplex effektív értékét, a b. esetben pedig a komplex
impedanciát. Észrevehető az ábrákon (melyet a (4.38-4.39) összefüggések
igazolnak), hogy mindegyik esetben az eredő komplex szám fázisban ![]() -vel siet a valós tengelyen felmért mennyiségekhez képest (a.
esetben az áramhoz, b. esetben az ohmos ellenállás valós értéke).
-vel siet a valós tengelyen felmért mennyiségekhez képest (a.
esetben az áramhoz, b. esetben az ohmos ellenállás valós értéke).
Vegyük egy kicsit a komplex impedanciát szemügyre. Felírhatjuk a valós impedanciát úgy, mint
|
|
|
és a feszültség és áram között kialakuló fázisszöget, mint
|
|
|
Rezonancia esetén (![]() )
) ![]() , vagyis (4.41)-ből
, vagyis (4.41)-ből ![]() , tehát az impedancia
valóssá válik és egyenlő az áramkör teljes ohmos ellenállásával,
, tehát az impedancia
valóssá válik és egyenlő az áramkör teljes ohmos ellenállásával, ![]() . A fenti feltételből meg lehet határozni azt a frekvencia
értéket (vagy adott frekvencia esetében azt a tekercs induktivitást vagy
kondenzátor kapacitást), amelynél rezonancia lép fel az áramkörben. A
frekvencia értékét megadó összefüggést Thomson-képletnek nevezzük.
. A fenti feltételből meg lehet határozni azt a frekvencia
értéket (vagy adott frekvencia esetében azt a tekercs induktivitást vagy
kondenzátor kapacitást), amelynél rezonancia lép fel az áramkörben. A
frekvencia értékét megadó összefüggést Thomson-képletnek nevezzük.
|
|
|
Az áramkörben folyó áram valós effektív értéke megadható, mint
|
|
|
amely rezonancia
esetén maximális ![]() értéket vesz fel.
értéket vesz fel.
Megjegyzés: rezonancia esetében, az áramköri paraméterek értékétől függően megtörténhet, hogy a tekercsen és kondenzátoron nagyobb feszültség jelenjen meg, mint a tápfeszültség, amely rezonancia esetén megegyezik az ellenálláson megjelenő feszültséggel.
|
|
|
A váltakozó áramú áramkörök esetében szokás megadni az áramkör jósági tényezőjét, amely nem más, mint rezonancia esetén, a tekercs (vagy kondenzátor) sarkain megjelenő feszültség és a tápfeszültség aránya:
|
|
|
Tekintsük a 18. ábrán látható
párhuzamos RLC áramkört, amelyben egy
![]() pillanatnyi értékkel
rendelkező váltakozó áramú áramforrás található. Ennek hatására az áramkör
főágában
pillanatnyi értékkel
rendelkező váltakozó áramú áramforrás található. Ennek hatására az áramkör
főágában ![]() pillanatnyi erősségű
áram folyik. Ahhoz, hogy ezt az áramot a komplex számok módszerével
meghatározhassuk, először meg kell határozzuk a feszültség komplex pillanatnyi
értékét:
pillanatnyi erősségű
áram folyik. Ahhoz, hogy ezt az áramot a komplex számok módszerével
meghatározhassuk, először meg kell határozzuk a feszültség komplex pillanatnyi
értékét: ![]() . Innen meghatározhatjuk a komplex effektív értéket:
. Innen meghatározhatjuk a komplex effektív értéket: ![]() . A továbbiakban használhatjuk az áramkör megoldásához a
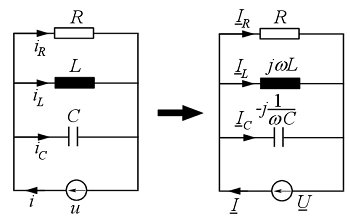
komplex pillanatnyi vagy effektív értéket, vagy a komplex amplitúdót is. A 18. ábrán
a komplex effektív értéket tüntettük fel.
. A továbbiakban használhatjuk az áramkör megoldásához a
komplex pillanatnyi vagy effektív értéket, vagy a komplex amplitúdót is. A 18. ábrán
a komplex effektív értéket tüntettük fel.
a. b.
18. ábra
Ezek után a váltakozó áramú ellenállásokat kell átírni komplex alakba, melyet a 19. ábrán tüntettünk fel (párhuzamosan kapcsolt váltakozó áramú ellenállások előnyösebb az admittanciák használata!) Az áramkörre a csomóponttörvényt a komplex mennyiségekkel a következő alakban írhatjuk fel:
|
ahol
tehát
|
|
A (4.46) összefüggésben szereplő
komplex impedanciát (![]() ) felírhattuk volna a komplex ellenállások párhuzamos
kapcsolásából származó eredő impedancia segítségével is:
) felírhattuk volna a komplex ellenállások párhuzamos
kapcsolásából származó eredő impedancia segítségével is:
|
|
|
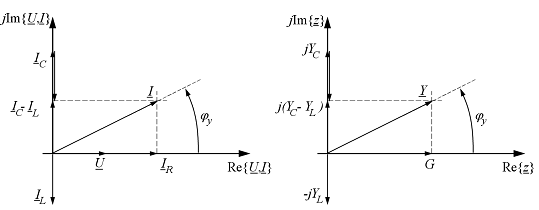
Figyelembe véve a 2.2. pont fáziseltolásokra vonatkozó eredményeit, illetve a komplex számoknak komplex számsíkban való ábrázolására vonatkozó szabályokat, megrajzolhatjuk a párhuzamos RLC áramkör fazorábráit (19.a-b ábrák).
Megjegyzés: Az ábrázolt esetben azt feltételeztük, hogy az áramkör induktív jellegű, az admittancia fázisszög pozitív. Ha az admittancia fázisszög nulla, az áramkörben rezonancia lép fel (párhuzamos RLC áramkörben egészen pontosan áramrezonanciának).
Az
19.a ábrán az áramköri ágakban folyó áramokat, illetve az áramforrás
feszültségét tüntettük fel, figyelembe véve, hogy az ellenálláson nincs fáziskülönbség,
a tekercsen késik ![]() -vel az áram a feszültséghez képest (komplex, míg a
kondenzátoron siet
-vel az áram a feszültséghez képest (komplex, míg a
kondenzátoron siet ![]() -vel az áram a feszültséghez képest. Ugyanezt végeztük el a
19.b ábrán a komplex admittanciákkal.
-vel az áram a feszültséghez képest. Ugyanezt végeztük el a
19.b ábrán a komplex admittanciákkal.
a. b.
19.a ábra
Elvégezve a műveleteket a komplex számokkal, az a. esetben
megkapjuk az áramkör főágában folyó áram erősségének effektív értékét, a b.
esetben pedig a komplex admittanciát. Észrevehető az ábrákon (melyet a (4.46-4.47)
összefüggések igazolnak), hogy mindegyik esetben az eredő komplex szám fázisban
![]() -al siet a valós tengelyen felmért mennyiségekhez képest (a.
esetben a feszültséghez, b. esetben a vezetőképesség).
-al siet a valós tengelyen felmért mennyiségekhez képest (a.
esetben a feszültséghez, b. esetben a vezetőképesség).
Vegyük egy kicsit a komplex impedanciát szemügyre. Felírhatjuk a valós impedanciát úgy, mint
|
|
|
és a feszültség és áram között kialakuló fázisszöget, mint
|
|
|
Rezonancia esetén (![]() )
) ![]() , vagyis (4.49)-ből
, vagyis (4.49)-ből ![]() , tehát az admittancia
valóssá válik és egyenlő az áramkör valós vezetőképességével,
, tehát az admittancia
valóssá válik és egyenlő az áramkör valós vezetőképességével, ![]() . A fenti feltételből következik, hogy a párhuzamos RLC
áramkörben ugyanolyan feltételek mellett teljesül a rezonancia, mint a soros
RLC áramkör esetében, illetve ugyanúgy definiálható a jósági tényező is.
. A fenti feltételből következik, hogy a párhuzamos RLC
áramkörben ugyanolyan feltételek mellett teljesül a rezonancia, mint a soros
RLC áramkör esetében, illetve ugyanúgy definiálható a jósági tényező is.
|
|
|
Találat: 5777