Közgazdaságtani jelölés- és képletgyűjtemény

JELÖLÉSEK:

L       - munka (Labour)

p - ár (Prise)

p_e - egyensúlyi ár

p_L      - a munka ára (= munkabér (w))

A - föld (mint termelési (ter 121d35b mészeti) tényező)

p_A      - föld ára (földbérleti díj)

r - kamat

K - tőke (beruházás)

p_K - a tőke ára (kamat)

E - vállalkozó

t - idő

P - profit (pi)

TP - teljes profit (Total Profit)

Q - termelési mennyiség (kibocsájtás v. Output)

q - keresleti-, kínálati mennyiség mennyiség (quantity)

S - kínálat (Supply)

D - kereslet (Demand)

dd      - egyéni kereslet

DD - piaci kereslet

Q^S - kínálati függvény

Q^D - keresleti függvény

Q_e      - egyensúlyi termelési mennyiség

e - árrugalmasság

TR - teljes bevétel (Total Revenue)

MR - határbevétel (Marginal Revenue)

AC - átlagköltség v. darabköltség (Average Cost)

TC - teljes költség (Total Cost)

FC - állandó költség (Fix Cost)

VC - változó költség (Variable Cost)

MC - határköltség (Marginal Cost)

AVC - átlagos változó költség (Average Variable Cost) - egy termékegységre jutó változó költség.

AFC - átlagos állandó költség (Average Fix Cost) - egy termékegységre jutó állandó (fix) költség.

FT - fogyasztói többlet

TT - termelői többlet

D - változás (delta)

I - jövedelem

U - közömbösségi görbe (függvény)

Tu      - összhaszon (Total utility)

Mu - határhaszon (Marginal utility)

MP - határtermék (Marginal Product)

AP - átlagtermék v. termelékenység (Average Product)

MFC - termelési tényező határköltség (Marginal Factor Cost)

MFC_L - a munka határköltsége (munka mint termelési tényező)

MRP - határtermék-bevétel (Marginal Revenue Product)

MRP_L - a munka határtermék-bevétele (munka mint termelési tényező)

FV_t - jövő érték (Future Value)

PV_t - jelen érték (Present Value)

NPV - nettó jelenérték (Net Present Value)

SZÁMÍTÁSOK:

KERESLET-KÍNÁLAT (keresleti függvény Q^D - kínálati függvény Q^S "Marschall kereszt" )

Pl. Egy termék piaci keresleti függvénye: Q = 400-2 p, a kínálati függvénye: Q = p-20

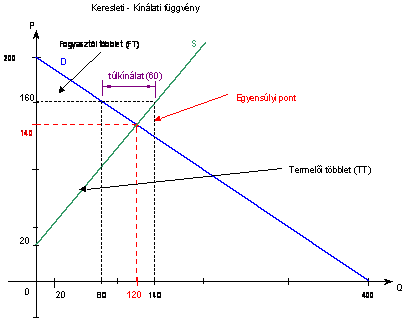
Egyensúlyi ár számítás: Az egyensúlyi árhoz tartozó keresett (egyensúlyi) mennyiség számítás:

Q^D = Q^S Q^D = Q^S

400 - 2xp = p - 20 / + 20 Q^D = 400 - 2x 140 = 400 - 280 = 120

420 = 3p / : 3 Q^S = 140 - 20 = 120

140 = p Qe = 120 (egyensúlyi mennyiség)

p_e = 140 (egyensúlyi ár)

Fogyasztói többlet számítás (FT):

A fogyasztói többlet ( FT ) az ár és a keresleti függvény (Q^D = 400 - 2 x p ) közé eső terület.

A fogyasztói többlet számítása a területszámításának képletéből T = a x b / 2 ahol "a" az egyik befogó,

"b" a másik befogó , majd ennek a négyszög a területét elosztjuk 2-vel mivel a derékszögű háromszög területe ennek a fele lesz.

A Q helyébe 0-t rendelünk. A keresleti ár 0 mennyiségnél: Q^D = 0, p = 200

( 200 - 140 ) x 120

A fogyasztó többlet: FT = = 3600

2

Termelői többlet számítás (TT):

A termelői többlet az ár és a keresleti függvény (Q^S = p - 20 ) közé eső terület

a termelő többlet számítása a területszámításának képletéből T = a x b / 2 ahol "a" az egyik befogó,

"b" a másik befogó , majd ennek a négyszög a területét elosztjuk 2-vel mivel a derékszögű háromszög területe ennek a fele lesz.

A kínálati függvény értéke az egyensúlyi árnál: Q^S = p - 20 = 140 - 20 = 120

(140 - 20) x 120

A termelői többlet: TT = = 7200

2

Az adott piac jellemzése:

Ha Q^D < Q^S = túlkínálat, az ár csökkenni fog

Q^D > Q^S = túlkereslet, hiány, az ár nővekedni fog

piaci egyensúlyi árnál (p_e) Q^D = Q^S

Ez Adam Smith a "láthatatlan kéz" elve.

ÁRRUGALMASSÁG

A kereslet árrugalmassága:

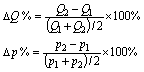
= rugalmatlan kereslet, (ha az ár nő, akkor a TR (összbevétel) nő)

= tökéletesen rugalmatlan kereslet,

= rugalmas kereslet, (ha az ár nő a bevétel csökken)

= egységnyi rugalmasság (maximális a bevétel TR_max),

= paradox árhatás (nő az ár, de mégis többet vesznek belőle = paradox árhatás)

A kereslet keresztár rugalmassága:

A kereslet - jövedelem rugalmassága:

HASZNOSSÁG

Hasznosság (haszon): =

A határhaszon (Marginal Utility): Mu =

Gossen II. törvénye: = az egy pénzegységnyi jövedelem határhaszna

azaz

Pl. két termék esetén, határhaszon számítás: Mu =, ,

Az x termék haszna = , az y termék haszna =

Összhaszon számítás: å Tu = TU_x + TU_y

Példa feladat

Egy fogyasztó 450 Ft-os jövedelemét x és y termékre költi. A két termék határhasznai függetlenek egymás és

más termékek elfogyasztott mennyiségétől. Mennyit vásároljon a racionális fogyasztó x-ből és y-ból,

ha a határhasznok és az egységárak a következők Px=100; Py=50.

Mennyi a fogyasztó összhaszna a két termék fogyasztásából ?

I = 450, Px=100, Py=50.

I = 450, Px=100, Py=50.

Megoldás: A fogyasztó először, másodszor és harmadszor is y-t (50,32,27)majd x-et választ ( ).

Az ötödik alkalomra ismét y-t vesz (23), a hatodik és hetedik termék kiválasztási sorrendje mindegy,

mivel egyforma a haszonnövekedés (20). A fogyasztó akkor választ optimálisan, ha 5 db y-t és 2 db x-et választ.

5* 50 = 250 Ft

2*100 = 200 Ft                                

250 Ft + 200 Ft = 450 Ft (I) A fogyasztó összhaszna: STU=TUx+TUy=4500+7000=11500

Költségek, amortizáció, profit:

Implicit költség = Amortizáció + Normál profit, másképpen: = Gazdasági költség - Explicit költség

Számviteli költség                               = Explicit költség + Amortizáció

Normál profit                                     = Implicit költség - Amortizáció

Számviteli profit                                  = Árbevétel - Számviteli költség

Gazdasági profit                                 = Árbevétel - Gazdasági költség

Rövidtávú vagy Parciális termelési függvényhez kapcsolodó számítások:

Határtermék

A munka határterméke:     diszkrét függvény esetében pontokból áll

folytonos függvénye: a q L szerinti deriváltja

pl.

A tőke határterméke:

diszkrét függvény esetében pontokból áll

folytonos függvénye:) a q K szerinti deriváltja (folytonos függvény) rövid távon nem értelmezhető!

Átlagtermék (termelékenység)

A munka átlagterméke:    

A tőke átlagterméke:

A parciális termelési függvény, táblázatos formában:

Költségek, költségfüggvények:

Állandó költség:      FC = K = tőke, p_K = r (kamat)

Változó költség: VC = = f(q) = az adott termelési függvénnyel

L = munka, p_L = munka ára = munkabér

pl. , tehát                         p_L = 1200

Teljes költség:                    TC = FC (fix költség)+VC (változó költség)    ,

ha nincs termelés tehát q = 0 akkor TC = FC , vagy

Határköltség: MC =

Határköltség tökéletes verseny esetén: MC = = = MC = p (ár)

MC =

Változó függvénye:       MC = (TC)¢q = (VC)'q                                  (VC= 0)

Átlagköltség:                                  AC =

Átlagos változó költség:     AVC =

Átlagos fix költség: AFC =

Bevételek, profit:

Határbevétel számítás tökéletes versenynél : MR = p

Profit számítás:                   egy vállalkozás megéri, ha TP >

Tökéletes versenynél: TR = p x q ; FC + VC_(q)

Profit maximum akkor van tökéletes versenynél ha teljesül az MR = MC feltétel

A vállalatok száma az adott iparágban: n =

Példa

Egy tökéletesen versenyző vállalat költségfüggvénye: TC = 0,25 q² + 100 q

A keresleti függvény: Q = 16000 - 10p. A termék ára: 120

Mennyit termel, és mekkora a profitja a tökéletesen versenyző vállalatnak?

Hány vállalat van az iparágban, ha a többi vállalat termelése is az adott költségfüggvénnyel értelmezhető?

Megoldás:

MC = (TC)¢q = (VC)'q                                                         (VC= 0)

MC = (0,25*q2 + 100*q )¢ = 0,5q + 100

p = 120

Tökéletes verseny esetén p (ár) = MC (határköltség)

p = MC

120 = 0,5q + 100              /-100

20 = 0,5q /: 0,5

40 = q

q = 40 ,tehát a vállalat által termelt mennyiség az adott termékből: 40

TR (összbevétel) = p*q (tökéletes versenynél)

TR = 120*40 = 4800               ,tehát a vállalat összes bevétele: 4800

TC (gazdasági költség) = 0,25*q² + 100*q = 0,25*(40)² + (100*40) = (0,25*1600) + 4000 = 400 + 4000 = 4400

,tehát a vállalat összes gazdasági költsége: 4400

TP (profit) = TR - TC = 4800 - 4400 = 400 ,tehát a vállalat profitja: 400

Q

Vállalatok száma az adott iparágban:    n =

q

ebből q = 40 és Q = 16000 - 10p = 16000 - (10*120) = 16000 - 1200 = 14800 mennyiség adható el összesen a termékből.

Q 14800

n = = = 370 ,tehát az adott piacon 370 vállalat van jelen.

q 40

Példa

Egy monopólium keresleti görbéje Q = 100 - 2*P. A teljes költség képlete TC = 20*Q.

Mennyi a vállalat optimális termelése? Milyen áron kínálja a terméket? Mennyi a vállalat profitja?

Megoldás:

Q = 100 - 2*P /*0,5

0,5*Q    = 50 - P /+P; -(-0,5*Q)

0,5*Q + P = 50

P = 50 - 0,5*Q MR (határbevétel) = 50 - Q ,mert ez a függvény kétszer meredekebb

MR = 50 - Q

MC = MR - P                       

TC = 20*Q MC (határköltség) = 20

MC      = MR

= 50 - Q /+Q

20 + Q = 50                /-20

Q^*        = 30 ,tehát a vállalat optimális termelése: 30

Q = 100 - 2*P

P^* = 50 - 0,5*Q = 50 - 0,5*30 = 50 - 15 = 35 , tehát a vállalat optimális kínálati ára: 35

T P (profit) = TR - TC = (P*Q) - TC = 30*35 - (20*30) = 1050 - 600 = 450 ,tehát a vállalat profitja: 450

P

D MC

P*

MR

Q

Q* (30)

A hosszútávú költség függvényhez kapcsolodó számítások:

TC = VC

TC = p_L x L + p_K x K                         ahol TC, p_L, p_K = konstans (állandó)

K =

Termelési tényezők piaca

Optimális tényező (input) felhasználás:

MRP = MFC              ,azaz a tényező határtermék bevétele = a tényező határköltségével

Optimális tényező (input) felhasználás tökéletes versenynél:

p_x ( termékár) = állandó (konstans), p_L ( munkaára, munkabér) = állandó (konstans)

Munka piaci optimalizálás:

MRP_L =

MFC_L = ,mert hosszú távon csak változó költség van TC = VC (FC = 0)

Tökéletes verseny esetében: MP_L x p_x = MRP_L (VMP_L) és p_L = MFC_L

Példa

Példa

p_x = 150 p_L = 400

q =

L = ?

q = ?

TP = ?

MP_L x p_x = p_L

L = 2,25

= 12

TP = (p_x x q) - (p_L x L) = (150 x 12) - (400 x 2,25) = 900

Példa

Egy termék piacán a kereslet és a kínálat a következő: p = 3775-5*Q, p = Q-725.

A termék termeléséhez szükséges input piacán a keresleti függvény: Q = 1800-3*p_i, a kínálati függvény Q = p_i -200.

A termék egyik előállítójának a termelési függvénye: q=-0,5*i²+36*i, míg határtermék függvénye: MP(i) = 36-i.

Hány terméket készítsen a vállalkozó és mennyi az optimális inputfelhasználás ?

                       

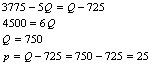
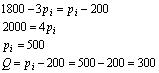
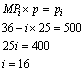
Optimális tényező (input) felhasználás monopólium esetében:

p_x ( termékár) = nem állandó , p_L ( munkaára, munkabér) = állandó (konstans)

,azaz tiszta monopólium a termékpiacon és tökéletes verseny a munkaerő piacon.

Ebben az esetben a termelési függvény kétszeres meredekségű !

Példa

Q^S = 2000 - 4p                      (kínálati függvény)

p_L = 225 (munkabér)

(keresleti függvény)

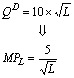,mert a termelési (kínálati) függvény kétszeres meredekségű !

L = ?

Q = ?

p_x = ?                          

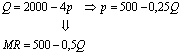kétszeres meredekség ! p_x =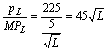

                                 

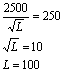
p_x = 500 - (0,25 x 100) = 475

TP = (p x Q) - (L x p_L) = (475 x 100) - (100 x 225) = 25.000

Jövő érték számítás:

FV_t = PV₀ x (1 + r)^t számolásnál: r (kamat) 20% = 0,2

r (kamat) 5% = 0,05

Példa

PV₀       = 50.000 Ft

r = 10% FV₃ = 50.000 x (1 + 0,1)³ = 66.500

t = 3 év

Jelen érték számítás (diszkontálás):

Nettó jelen érték számítás (Beruházási döntés) :

nettó jelenérték

Példa

r = 20%

K₀ = 10 Millió (induló beruházás)

K₁ =   4 Millió (1. évi beruházás)

K₂ =   4 Millió (2. évi beruházás)

K₃ =   4 Millió (3. évi beruházás)

a beruházás nettó jelenértéke negatív, azaz a beruházás 3 év alatt nem megtérülő mert a hozama kisebb mintha a bankban tartanák az erre fordított pénzünket.

Példa

Megéri-e az a beruházás, amely 30 millióba kerül és az első két évben évi 5 milliót, majd további négy évig

évi 13 milliót hoz. A kamatláb az első három évben évente 25 %, majd a továbbiakban évi 12 %-ra csökken ?

r _1,2,3 = 25 % ; r _4,5,6 = 12 %    NPv = ( nettó jelenérték = jővőbeli hozamok jelenértéke - beruházás)

A beruházás nem éri meg mivel NPv (nettó jelenérték) negatív.