| kategória | ||||||||||
|
|
||||||||||
|
|
||
Relációs algebra, relációs teljesség
1. Bevezetés
A praktikus alkalmazások szempontjából a relációs adatmodell a legfontosabb a modellek közül. Sikerének titka egyszerűsége, érthetősége, és a hozzá kapcsolódó számos művelet. S bár kifejezőereje jó, hatékonysága hozzá képest alulmarad.
Alapja a síkbeli, kétdimenziós táblázat, a reláció. A reláció a táblákkal analóg, mert a kapcsolatokat ezek segítségével lehet leírni. A reláció elemei a sorok, a táblázat fejlécében pedig az attribútumok szerepelnek.
Példa: FILM
|
CÍM |
ÉV |
SZALAGFAJTA |
|
||
|
= r rek. |
|
|
|
||
|
|
|
|
|
Def.: Reláció
A reláció egy síkbeli tábla, ami pedig egy direkt szorzat egy részhalmaza, amelyben a sorok (rekordok) sorrendje lényegtelen. Felfogható úgy is, mint Attribútum -> Érték függvények halmaza, ahol az oszlopok (= attribútumok) sorrendje irreleváns.
A fenti példában:
FILM CÍM ÉV SZALAGFAJTA
r(CÍM)="Óz"
Def.: Nézet
. Szintén egy síkbeli táblázat:
R
|
R(A1,A2,...Ak) |
A2 |
|
Ak |
||
|
|
|
|
|
. ~R D1 D2 Dk, ahol Di az Ai értékkészlete. (A sorok sorrendje nem számít.)
. A sor egy f ÈDi függvény. (Az oszlopok sorrendje nem számít.)
2. A relációs adatmodell alapműveletei (E.F. Codd, '70)
. halmazműveletek
únió (Jele: È
Adott két reláció: R és S.
RÈS az R és S sorait jelenti.
A műveltnek nincs mindig értelme, ezért megfogalmazhatunk - nem kötelező érvényű - követelményeket az únióval kapcsolatban:
legyen R és S oszlopszáma egyenlő!
esetleg oszlopaik típusa is feleljen meg egymásnak!
Példa
R
|
A |
B |
|
a |
a |
|
a |
c |
|
b |
c |
S
|
A |
D |
|
a |
a |
|
a |
d |
|
a |
c |
|
b |
b |
RÈS
|
A |
|
|
a |
a |
|
a |
c |
|
b |
c |
|
a |
d |
|
b |
b |
Ahogy a példában is látszik, előfordulhat, hogy az únióban hiányozni fog egy attribútumnév (oszlopfejléc). Az ismétlődő sorok általában nem megengedettek (pl.: (a,a) ) az únióban, mivel a relációs világ értékorientált, és a redundanciát igyekszik kiiktatni ott, ahol lehet.
különbség (Jele: \)
Adott két reláció: R és S.
R\S elemei R azon sorai lesznek, amelyek nem szerepelnek S-ben.
R\S örökli az R oszlopszámát, attribútumait, típusait.
Példa: az úniónál bemutatott R-re és S-re
R\S
|
A |
B |
|
b |
c |
direkt szorzat (Descartes-szorzat, jele:
Adott két reláció: R (k oszlopa és m sora van) és S (l oszlopa és n sora van).
R S-nek (k+l) számú oszlopa lesz, amikor a direkt szorzat-képzés során R sorait kiegészítjük az S soraival az összes lehetséges módon. Tehát R S-nek m n számú sora lesz.
R S(A1,...Ak,B1,...,Bl)
S(B1,...,Bl)
Példa: az úniónál bemutatott R-re és S-re k=l=2 k+l=4
R S
|
A |
B |
A' |
D |
|
a |
a |
a |
a |
|
|
|
|
|
|
|
|
b |
b |
|
a |
c |
a |
a |
|
|
|
|
|
Az alapműveletek közül ez a legnehezebb és leglassabb. Bár polinom időben elvégezhető, mégis ez aleginkább időigényes művelet.
. relációs műveletek
szelekció (Jele: sF(R)[1])
A szelekció egy adott R relációra és F formulára vonatkozik.
sF(R) az R reláció azon sorait jelenti, amelyekre F formula igaz. Örökli a típusokat és attribútumokat.
F alakja (Codd eredeti javaslata szerint): AQB, AQc, cQA, ahol:
A és B attribútumnevek,
c egy konkrét érték,
Q pedig elemi összehasonlító operátorok halmaza: Q
Ezeket az F formulákat atomoknak nevezzük. Az atomok kombinálhatók a ØÙ jelekkel.
Példa sA=D(S) s(A=B) (A¹b)(R)
|
A |
D |
|
a |
a |
|
b |
b |
|
A |
B |
|
a |
a |
|
a |
c |
A szelekció eredménye sosem egy elemi objektum, hanem általános esetben egy reláció, azaz sorok kollekciója.
vetítés (projekció) (Jele: P
A PAi1,...Ail(R) vetítés az R vetítését végzi el az Ai1,...Ail oszlopokra:
paramétere egy R reláció;
meg kell adni R biznoyos attribútumait is (Ai1,...Ail);
bizonyos oszlopokat elhagy a fenti R relációból;
és megváltoztatja az oszlopok sorrendjét.
Szemantikája egyszerű
1. vegyük az R Ai1,...Ail oszlopait ebben a sorrendben;
2. hagyjuk el R többi oszlopát;
3. hagyjuk el az esetleges ismétlődéseket is.
Példa PA(R)
|
A |
|
a |
|
b |
A relációs alapműveletek relációkat adnak eredményül, ezért ezen relációs műveletek egymással kombinálhatók. Pl.: sA<D(R S), ez először egy Descartes-szorzást, majd egy szelekciót jelöl.
3. A relációs adatmodell további fontos műveletei
metszet (Jele:
Adott két reláció: R és S.
R S sorai azok a sorok lesznek, melyek R-nek és S-nek is sorai.
Formálisan: R S=R\(R\S)=S\(S\R)
Példa: az úniónál megismert R-re és S-re
R S
|
A |
B |
|
a |
a |
|
a |
c |
Az attribútumok öröklődése itt kétféle lehet.
![]()
![]()
![]()
![]() természetes illesztés (összekapcsolás, join)
(Jele: )
természetes illesztés (összekapcsolás, join)
(Jele: )
Adott két reláció, R és S. Az természetes illesztés művelete bármely két halmazra értelmes operáció.
![]()
![]()
![]()
![]() R S kiszámítása attól függ, hogy melyek a
közös attribútumnevek a relációkban:
R S kiszámítása attól függ, hogy melyek a
közös attribútumnevek a relációkban:
R(A1,...Ak,B1,...,Bs)
S(A1,...Ak,C1,...,Cd)
vagyis az Ai-k a közös attribútumnevek.
Az R S-ből indulva vesszük azokat a sorokat, amelyekre igaz, hogy R.Ai=S.Ai.
Az eredményt vetítjük rá R.A1,...,R.Ak,C1,...,Cd,B1,...,Bs-re.
Tulajdonságai
![]()
![]()
![]()
![]() Az így kiadódó
R S -nek (k+s+d) számú oszlopa
lesz.
Az így kiadódó
R S -nek (k+s+d) számú oszlopa
lesz.
Örököl attribútumokat és típusokat is.
k=0 esetén egyszerű szorzatműveletet jelent.
![]()
![]()
![]()
![]() Kifejezhető
alapműveletekkel (a gyakorlatban igyekszünk másként megkapni az egyesítés
eredményét): R S = PA1,...Ak,B1,...,Bs,C1,...,Cd sAi=Ai'(R S)). A vetítésnél nem kell
az azonos sorokat törölni.
Kifejezhető
alapműveletekkel (a gyakorlatban igyekszünk másként megkapni az egyesítés
eredményét): R S = PA1,...Ak,B1,...,Bs,C1,...,Cd sAi=Ai'(R S)). A vetítésnél nem kell
az azonos sorokat törölni.
Példa: k=1, s=2,d=1, (k+s+d)=4
R
|
A |
B |
C |
|
a |
b |
|
|
a |
c |
|
|
b |
c |
|
R S S
|
|
C |
|
a |
|
|
b |
|
|
x |
|
|
A |
B |
C |
D |
|
a |
b |
|
a |
|
a |
b |
|
x |
|
a |
c |
|
b |
![]()
![]()
![]() félillesztés (Jele: )
félillesztés (Jele: )
Technikai szerepe van a lekérdezési optimalizátorokban (elosztott rendszerekben).
![]()
![]()
![]()
![]()
![]()
![]()
![]() R S = PR(R S).
R S = PR(R S).
Általános (Q illesztés
Adott két reláció: R és S.
A az R, B az S reláció attribútuma.
![]()
![]()
![]()
![]() R S jelentése: sAQ B(R S)
R S jelentése: sAQ B(R S)
A Q B
Ebben az esetben tehát nem egyenlőségre, hanem általános műveletre végezzük el az illesztést.
![]()
![]()
![]()
![]() Példa: R S
Példa: R S
R.C<S.C
|
A |
B |
R.C |
D |
S.C |
|
a |
b |
|
b |
|
Def.: Relációs teljesség
Egy relációs lekérdező nyelvet relációsan teljesenek nevezünk, ha benne az öt alapművelet (únió, különbség, direkt szorzat, szelekció, vetítés) megvalósítható. Az SQL relációsan teljes.
Egyes komoly lekérdező nyelvek ezen minimális követelményeket túl is teljesítik, azaz nem csak relációs, hanem aggregációs műveletekre is képesek.
Def.: Aggregáció
Az összesítő műveleteket, melyek egy relációból elemi értéket állítanak elő, aggregációknak nevezzük. Például.: AVG (átlag), MIN (minimum), MAX (maximum), CNT (számlálás), SUM (összegzés).
Példa: DOLGOZÓ(SzemélyiSzám, Fizetés,...)
FCNT Szemszám, AVG Fizetés(DOLGOZÓ) eredménye egy számpár lesz. Megkapjuk a dolgozók számát és az átlagos fizetést.
4. NULL értékek problematikája
A NULL értékek kitöltetlen attribútum-értékeket jelentenek.
Például: TERMELŐ(Név,Cím,Termék,Ár)
(Rezeda Kázmér,NULL,Zab,300)
sCím="Budapest"(TERMELŐ)
A NULL érték jelentése azonban nem homogén. Jelentheti azt, hogy
létezik ugyan az attribútum-érték, de nem ismerjük (ez a megengedő álláspont), vagy hogy
az érték nem létezik (ez a nem megengedő álláspont).
Műveletek NULL értékekkel
![]()
![]()
![]()
![]()
![]()
![]() Baloldali külső illesztés (Jele: )
Baloldali külső illesztés (Jele: )
![]()
![]()
![]()
![]()
![]()
![]() Az R S baloldali külső illesztésben R minden
sora megjelenik, esetleg NULL értékkel S-nél.
Az R S baloldali külső illesztésben R minden
sora megjelenik, esetleg NULL értékkel S-nél.
Példa
R S
![]()
|
A |
B |
|
a |
b |
|
a |
c |
|
B |
C |
|
b |
d |
|
e |
e |
|
|
B |
C |
|
a |
b |
d |
|
a |
c |
NULL |
Ennek a műveletnek az univerzális relációs megközelítésnél van szerepe, ahol az univerzális relációban minden attribútum szerepel.
![]()
![]()
![]()
![]()
![]()
![]() Jobboldali külső illesztés (Jele: )
Jobboldali külső illesztés (Jele: )
Benne fordított a szereposztás R-re és S-re nézve.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Teljes külső illesztés (Jele: )
Teljes külső illesztés (Jele: )
Benne a teljes R és S megjelenik.
Példa:
|
R S |
B |
C |
||
|
|
b |
d |
||
|
a |
c |
NULL |
||
|
NULL |
e |
e |
Külső únió (Jele: Èk
Részben È-kompatibilis relációk egyesítését jelenti.
Példa: DIÁK(Név,Témavezető,Tanszék)
TANÁR(Név,Tanszék,Beosztás)
DIÁK Èk TANÁR eredménye:
|
diák tanár |
Tanszék |
Beosztás |
Témavez. |
||
|
|
|
NULL |
|
||
|
|
|
|
NULL |
Def.: Univerzális reláció
Az összes alapreláció (azaz a sémában ténylegesen tárolt reláció) külső úniója az univerzális reláció.
5. E/K séma - relációs séma átalakítás
Az átalakításra van egy teljesen gépies út, ami azonban nem adja mindig a legjobb megoldást.
Egyed: E(A1,...,Ak) R(A1,...,Ak) Reláció
Az egyed egy az egyben átalakítható relációvá (k-oszlopos táblává).
R(A1,...,Ak)
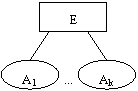
Bonyolultabb átalakítás
R(A1,...,As, B1,...,Bl,..., S1,...,St)
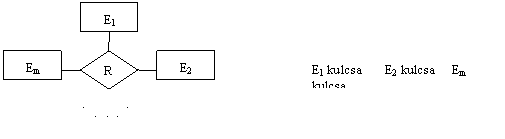
Hogyan kaphatunk jó átalakított relációs sémát?
ábrázoljunk minden információ-elemet!
a fontos igényeket kifejező műveletek legyenek hatékonyak! Például: ne kelljen túl sok helyről összeszedni egy fontos lekérdezés adatait.
:
3023