| kategória | ||||||||||
|
|
||||||||||
|
|
||
|
|||||||||||
Matematika A1 vizsga elméleti kérdések
Definíciók
1. Peano-axiómák
A természetes számok halmazát (N) a Peano-axiómák segítségével definiáljuk.
1. r az N-nek N-re történő bijektív leképezése
![]() )
)
![]() és
és ![]() és
és ![]() esetén
esetén ![]() , akkor
, akkor ![]()
![]()
A rákövetk 121j97b ezés-függvény ![]() :
:
![]() ;
; ![]()
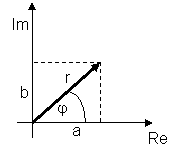
2. Komplex számok n-edik gyökének meghatározása, áttérés algebrai alakról trigonometrikus alakra.
Komplex számok n-edik gyökének meghatározása trigonometrikus alakban célszerű. Az
algebrai alak: ![]() , a trigonometrikus alak:
, a trigonometrikus alak: ![]() .
.
Az áttérést algebrai alakról trigonometrikus alakra a Moivre-formulák segítségével végezzük:
![]() ;
; ![]() ;
; ![]()
Komplex szám n-edik gyökének meghatározása:
![]() , ahol
, ahol ![]() ;
;
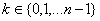
A gyökök a komplex számsíkon egy origó
középpontú, ![]() sugarú körbe írt
szabályos n-oldalú sokszög csúcsaiban
helyezkednek el.
sugarú körbe írt
szabályos n-oldalú sokszög csúcsaiban
helyezkednek el.
3. Valós számsorozat definíciója, legalább 3 nevezetes sorozat felsorolása és rövid jellemzésük.
Valós számsorozaton olyan függvényt értünk, melynek értelmezési tartománya a nemnegatív valós számok halmaza (N+), értékkészlete pedig a valós számok halmaza (R ).
- megadása lehet explicit (pl. ![]() ) vagy rekurzív (pl.
) vagy rekurzív (pl. ![]() )
)
Nevezetes sorozatok:
![]() (
(![]() )
)
Bizonyítás: Bernoulli-egyenlőtlenség segítségével
![]() (
(![]() )
)
A
sorozat korlátos és konvergens: ![]()
Bizonyítás: rendőr-elvvel
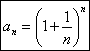 (
(![]() A sorozat korlátos ,
szigorúan monoton növekvő és konvergens:
A sorozat korlátos ,
szigorúan monoton növekvő és konvergens: ![]()
4. Valós számsorozat határértéke (minden típusának megadása)
Egy valós ![]() számsorozat konvergens, ha
számsorozat konvergens, ha ![]() esetén
esetén ![]() küszöbszám, melyre
küszöbszám, melyre ![]() esetén
esetén ![]() . Ilyenkor az a valós
számot a sorozat határértékének nevezzük.
. Ilyenkor az a valós
számot a sorozat határértékének nevezzük.
Jelölése: ![]() vagy
vagy ![]() .
.
Ha egy sorozatnak létezik véges határértéke, akkor konvergensnek, ha nem létezik, akkor divergensnek mondjuk.
Egy valós ![]() számsorozat végtelenhez divergál, ha
számsorozat végtelenhez divergál, ha ![]() esetén
esetén ![]() küszöbszám, melyre
küszöbszám, melyre ![]() esetén
esetén ![]() . Jelölése:
. Jelölése: ![]() vagy
vagy ![]() .
.
Egy valós ![]() számsorozat a mínusz végtelenhez divergál, ha
számsorozat a mínusz végtelenhez divergál, ha ![]() esetén
esetén ![]() küszöbszám, melyre
küszöbszám, melyre ![]() esetén
esetén ![]() . Jelölése:
. Jelölése: ![]() vagy
vagy ![]() .
.
5. Függvény fogalma, értelmezési tartománya, értékkészlete
Ha A
halmaz minden egyes eleméhez hozzárendeljük B
halmaz pontosan egy elemét, akkor ezt a leképezést függvénynek nevezzük.
Jelölése: ![]()
Az értelmezési tartomány azon elemek halmaza,
melyekhez a függvény hozzárendel egy-egy elemet a B halmazból. Jele: ![]()
Az értékkészlet azon B-beli elemek halmaza, melyeket f
ténylegesen hozzárendel A valamelyik
eleméhez. Jele: ![]()
6. Egyváltozós valós-valós függvények határértéke
Cauchy-féle definíció:
Legyen az egyváltozós valós-valós f függvény (![]() ) értelmezve az x0
pont valamely környezetében. Az f
függvény határértéke x0
helyen létezik és értéke A akkor és
csak akkor, ha
) értelmezve az x0
pont valamely környezetében. Az f
függvény határértéke x0
helyen létezik és értéke A akkor és
csak akkor, ha ![]() esetén
esetén ![]() úgy, hogy ha
úgy, hogy ha ![]() akkor
akkor ![]()
Heine-féle definíció:
Legyen az egyváltozós valós-valós f függvény (![]() ) értelmezve az x0
pont valamely környezetében. Az f függvény határértéke x0 helyen létezik és értéke A akkor és csak akkor, ha
) értelmezve az x0
pont valamely környezetében. Az f függvény határértéke x0 helyen létezik és értéke A akkor és csak akkor, ha ![]() valós számsorozatra,
ahol
valós számsorozatra,
ahol ![]() és
és ![]() , teljesül, hogy
, teljesül, hogy ![]()
7. Egyváltozós valós-valós függvény folytonossága
Legyen az egyváltozós valós-valós f függvény (![]() ) értelmezve az x0
pont valamely környezetében. Az f függvényt x0
helyen folytonosnak nevezzük, ha
) értelmezve az x0
pont valamely környezetében. Az f függvényt x0
helyen folytonosnak nevezzük, ha ![]() esetén
esetén ![]() úgy, hogy ha
úgy, hogy ha ![]() , akkor
, akkor ![]()
8. Egyváltozós valós-valós függvény differenciálszámítása
Egy egyváltozós valós-valós függvény
differenciálható (deriválható) az x0
pontban és differenciál-hányadosa (deriváltja) A akkor és csak akkor, ha a ![]() határérték létezik és
véges.
határérték létezik és
véges.
A definíció lineárisan megfogalmazva:
Legyen az egyváltozós valós-valós f függvény (![]() ) értelmezve az x0
pont valamely környezetében. A függvény deriválható az x0 pontban akkor és csak akkor, ha
) értelmezve az x0
pont valamely környezetében. A függvény deriválható az x0 pontban akkor és csak akkor, ha ![]() és
és ![]() függvény úgy, hogy
függvény úgy, hogy ![]() és ha
és ha ![]() , akkor
, akkor ![]() . Ilyenkor az A
számot az f függvény x0 helyen vett differenciálhányadosának
nevezzük.
. Ilyenkor az A
számot az f függvény x0 helyen vett differenciálhányadosának
nevezzük.
9. Egyváltozós valós-valós függvény monotonitása, konvexitása
Az egyváltozós valós-valós f függvényt (![]() ) az x0 helyen
) az x0 helyen
a) monoton növekvőnek
b) szigorú monoton növekvőnek
c) monoton csökkenőnek
d) szigorú monoton csökkenőnek
nevezzük, ha x0 egy ![]() sugarú környezetére (
sugarú környezetére (![]() ) igaz, hogy
) igaz, hogy ![]() számokra
számokra
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Legyen az egyváltozós valós-valós f függvény (![]() ) x0
helyen deriválható, és x0
) x0
helyen deriválható, és x0 ![]() sugarú környezetében
értelmezhető (
sugarú környezetében
értelmezhető (![]() ). A függvényt x0
helyen
). A függvényt x0
helyen
a) konvexnek
b) konkávnak
mondjuk, ha ![]() esetén
esetén
a) ![]()
b) ![]()
10. Lokális szélsőérték és inflexiós pont definíciója
Az egyváltozós valós-valós f függvénynek (![]() ) x0
helyen
) x0
helyen
a) lokális minimuma
b) lokális maximuma
van, ha x0-nak
létezik egy olyan ![]() környezete, amelyre
környezete, amelyre ![]() esetén
esetén
a) ![]()
b) ![]()
Ha egy egyváltozós valós-valós f függvénynek (![]() ) egy adott pontban létezik érintője, és ebben a pontban a
függvény se nem lokálisan konvex, se nem lokálisan konkáv, akkor ezt a pontot a
függvény inflexiós pontjának nevezzük.
) egy adott pontban létezik érintője, és ebben a pontban a
függvény se nem lokálisan konvex, se nem lokálisan konkáv, akkor ezt a pontot a
függvény inflexiós pontjának nevezzük.
11. Riemann szerinti integrálhatóság fogalma
Legyen az f
egyváltozós valós-valós függvény (![]() ) korlátos az
) korlátos az ![]() intervallumon. Az f függvény Riemann szerint integrálható
az
intervallumon. Az f függvény Riemann szerint integrálható
az ![]() intervallumon, ha az
intervallum minden lehetséges
intervallumon, ha az
intervallum minden lehetséges ![]() felosztásához tartozó
alsó illetve felső integrálközelítő összegeinek (
felosztásához tartozó
alsó illetve felső integrálközelítő összegeinek (![]() és
és ![]() ) szuprémuma illetve infinuma megegyezik, vagyis ha
) szuprémuma illetve infinuma megegyezik, vagyis ha ![]() .
.
![]() ;
; ![]()
Az alsó integrálközelítő összeg: ![]() , ahol mi
az f függvény minimuma
, ahol mi
az f függvény minimuma ![]() felosztás i-edik részintervallumán.
felosztás i-edik részintervallumán.
A felső integrálközelítő összeg: ![]() , ahol Mi
az f függvény maximuma
, ahol Mi
az f függvény maximuma ![]() felosztás i-edik részintervallumán.
felosztás i-edik részintervallumán.
12. Határozott integrál, primitív függvény
Ha egy egyváltozós valós-valós f függvény (![]() ) Riemann-integrálható az
) Riemann-integrálható az ![]() intervallumon, akkor
az alsó és felső integrálközelítő összegeinek közös felső- illetve alsó korlátját
(az
intervallumon, akkor
az alsó és felső integrálközelítő összegeinek közös felső- illetve alsó korlátját
(az ![]() számot, lsd előző pont) az f függvény
számot, lsd előző pont) az f függvény ![]() intervallumon vett
határozott integráljának nevezzük. Jelölése:
intervallumon vett
határozott integráljának nevezzük. Jelölése: 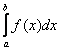
Egy egyváltozós valós-valós f függvény (![]() ) primitív függvényének nevezzük azt az F függvényt (
) primitív függvényének nevezzük azt az F függvényt (![]() ), amely az értelmezési tartomány minden pontjában
differenciálható, és
), amely az értelmezési tartomány minden pontjában
differenciálható, és ![]() esetén
esetén ![]()
13. Improprius integrálok fő típusainak definíciói
Legyen adott egy egyváltozós valós-valós f függvény (![]() ), melyre minden
), melyre minden ![]() esetén
esetén ![]() (
(![]() ). Ekkor az
). Ekkor az 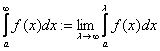 kifejezést az f függvény improprius integráljának
nevezzük, feltéve, ha a jobb oldalon álló határérték létezik és véges.
kifejezést az f függvény improprius integráljának
nevezzük, feltéve, ha a jobb oldalon álló határérték létezik és véges.
Hasonlóan értelmezzük az 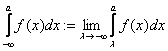 improprius integrált
is.
improprius integrált
is.
Legyen adott egy egyváltozós valós-valós f függvény (![]() ), melyre minden
), melyre minden ![]() esetén
esetén ![]() (
(![]() ). Ekkor az
). Ekkor az 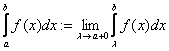 kifejezést az f függvény improprius integráljának
nevezzük, feltéve, ha a jobb oldalon álló határérték létezik és véges.
kifejezést az f függvény improprius integráljának
nevezzük, feltéve, ha a jobb oldalon álló határérték létezik és véges.
Hasonlóan értelmezzük az 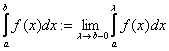 improprius integrált
is.
improprius integrált
is.
Tételek
1.Bernoulli-egyenlőtlenség és legalább egy alkalmazása
Bernoulli-egyenlőtlenség: ![]() ; (
; (![]()
Alkalmazási példa:
1. ![]() (
(![]() ) sorozat végtelenbe divergálásának bizonyítása.
) sorozat végtelenbe divergálásának bizonyítása. ![]() . A jobboldali kifejezés (Bernoulli-egyenlőtlenség
segítségével adódik) monoton növekvő számtani sorozat, ami végtelenbe divergál,
tehát az eredeti sorozat is. (
. A jobboldali kifejezés (Bernoulli-egyenlőtlenség
segítségével adódik) monoton növekvő számtani sorozat, ami végtelenbe divergál,
tehát az eredeti sorozat is. (![]() )
)
![]() korlátosságának
bizonyítása
korlátosságának
bizonyítása
2. Bolzano és Weierstrass tételei
Weierstrass-tétel: Legyen az f (![]() ) függvény folytonos az
) függvény folytonos az ![]() intervallumon (
intervallumon (![]() ), ekkor létezik olyan
), ekkor létezik olyan ![]() úgy, hogy
úgy, hogy ![]() esetén
esetén ![]()
Bolzano-tétel:
Legyen az f függvény folytonos
az ![]() intervallumon (
intervallumon (![]() ), ekkor a függvény felveszi az
), ekkor a függvény felveszi az ![]() és
és ![]() közötti összes
értéket.
közötti összes
értéket.
3. Inverz függvény differenciálási szabálya
Legyen az f (![]() ) függvény deriválható az
) függvény deriválható az ![]() pontban és
invertálható az a pont környezetében.
Tegyük fel, hogy
pontban és
invertálható az a pont környezetében.
Tegyük fel, hogy ![]() . Ekkor ebben a környezetben az inverz függvény (
. Ekkor ebben a környezetben az inverz függvény (![]() differenciálható, és
differenciálható, és ![]() (
(![]() ,
, ![]() )
)
Más alakban: ![]()
4. Az összetett függvény differenciálási szabálya
Adottak f
és g (![]() ) függvények (
) függvények (![]() ). Legyen f
függvény deriválható az
). Legyen f
függvény deriválható az ![]() pontban, g pedig deriválható az x0 pontban. Ekkor az
pontban, g pedig deriválható az x0 pontban. Ekkor az ![]() összetett függvény is
deriválható az x0 pontban
(láncszabály):
összetett függvény is
deriválható az x0 pontban
(láncszabály):
![]()
Más alakban: ![]()
5. Rolle tétele és egy példa az alkalmazására
Rolle-féle középértéktétel: Legyen az f
(![]() ) függvény differenciálható az
) függvény differenciálható az ![]() intervallumon, és
intervallumon, és ![]() . Ekkor
. Ekkor ![]() úgy, hogy
úgy, hogy ![]()
Geometriai jelentése: Az intervallumon létezik olyan pont, ahol a függvény érintője párhuzamos az x tengellyel.
Alkalmazási példa: a Cauchy-féle középértéktétel bizonyítása
6. Lagrange-féle középértéktétel
Legyen az f (![]() ) függvény differenciálható az
) függvény differenciálható az ![]() intervallumon. Ekkor
intervallumon. Ekkor ![]() úgy, hogy
úgy, hogy ![]()
Geometriai jelentése: Ha ![]() és
és ![]() , akkor az intervallumon létezik olyan pont, ahol a függvény
érintője párhuzamos az AB húrral.
, akkor az intervallumon létezik olyan pont, ahol a függvény
érintője párhuzamos az AB húrral.
7. Cauchy-féle középértéktétel
Legyenek az f és g (![]() ) függvények deriválhatók az
) függvények deriválhatók az ![]() intervallumon és
tegyük fel, hogy
intervallumon és
tegyük fel, hogy ![]() ;
;![]() esetén. Ekkor
esetén. Ekkor ![]() úgy, hogy
úgy, hogy ![]()
8. Lokális szélsőérték létezésének elégséges feltétele
Legyen az f (![]() ) függvény differenciálható az
) függvény differenciálható az ![]() intervallumon és a
intervallumon és a ![]() helyen
helyen ![]() . Ha
. Ha ![]() esetén
esetén ![]() és
és ![]() esetén
esetén ![]() , akkor az f
függvénynek
, akkor az f
függvénynek ![]() helyen lokális
maximuma van.
helyen lokális
maximuma van.
Ha a tételben a két relációjelet megfordítjuk, a lokális minimum létezésének elégséges feltételét kapjuk.
9. Lokális konvexitás elégséges feltétele
Legyen az f (![]() ) függvény legalább kétszer differenciálható az x0 pontban és annak egy
környezetében. Ekkor ha
) függvény legalább kétszer differenciálható az x0 pontban és annak egy
környezetében. Ekkor ha ![]() , akkor az f
függvény x0 pontban konvex,
ha pedig
, akkor az f
függvény x0 pontban konvex,
ha pedig ![]() , akkor konkáv.
, akkor konkáv.
10. Az inflexiós pont létezésének elégséges feltétele
Legyen az f (![]() ) függvény legalább kétszer differenciálható az x0 pontban és annak egy
környezetében, továbbá
) függvény legalább kétszer differenciálható az x0 pontban és annak egy
környezetében, továbbá ![]() . Ekkor ha
. Ekkor ha ![]() az x0 helyen előjelet vált,
akkor az f függvénynek x0 helyen inflexiós pontja
van.
az x0 helyen előjelet vált,
akkor az f függvénynek x0 helyen inflexiós pontja
van.
11. Bernoulli-L'Hospital szabály
Legyenek az f és g (![]() ) függvények differenciálhatók az x0 pont egy környezetében, továbbá
) függvények differenciálhatók az x0 pont egy környezetében, továbbá ![]() valamint
valamint ![]() . Ekkor
. Ekkor ![]() , amennyiben ez utóbbi határérték létezik és véges, vagy
, amennyiben ez utóbbi határérték létezik és véges, vagy ![]() .
.
Megjegyzések:
12. Newton-Leibniz szabály
Legyen az f (![]() ) függvény integrálható, az F (
) függvény integrálható, az F (![]() ) függvény pedig folytonos az
) függvény pedig folytonos az ![]() intervallumon és
differenciálható az
intervallumon és
differenciálható az ![]() intervallumon, továbbá
intervallumon, továbbá
![]() esetén
esetén ![]() . Ekkor
. Ekkor 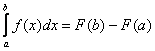
13. Helyettesítéses és parciális integrálás elve
Helyettesítéses integrálás:
Legyen az ![]() (
(![]() ) függvény differenciálható a K intervallumon, továbbá
létezik az f(x) (
) függvény differenciálható a K intervallumon, továbbá
létezik az f(x) (![]() ) függvénynek a
) függvénynek a ![]() intervallumon primitív
függvénye:
intervallumon primitív
függvénye: ![]() (
(![]() . Ekkor
. Ekkor ![]() függvénynek is létezik
primitív függvénye:
függvénynek is létezik
primitív függvénye: ![]()
Parciális integrálás:
Legyenek f
és g (![]() ) differenciálható függvények H halmazon, valamint
) differenciálható függvények H halmazon, valamint ![]() -nak létezik itt primitív függvénye. Ekkor
-nak létezik itt primitív függvénye. Ekkor ![]()
Határozott integrállal: Legyenek ![]() és
és ![]() függvények
integrálhatók
függvények
integrálhatók ![]() intervallumon. Ekkor
intervallumon. Ekkor 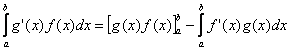
14. Ívhossz, forgástest térfogat, forgástest palást, szektorterület kiszámítása
Ívhossz kiszámítása: Legyen az f függvény (![]() ) folytonos és integrálható az
) folytonos és integrálható az ![]() intervallumon. Legyen
intervallumon. Legyen ![]() és
és ![]() . Ekkor az AB ív
hossza:
. Ekkor az AB ív
hossza: 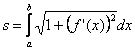 ;
;
Paraméteresen adott
függvény esetén (![]() ):
): 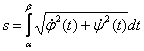
Forgástest térfogatának kiszámítása: Legyen az
f függvény (![]() ) folytonos és integrálható az
) folytonos és integrálható az ![]() intervallumon.
Forgassuk meg a függvény görbéjét az x tengely körül. Az így kapott forgástest
térfogata:
intervallumon.
Forgassuk meg a függvény görbéjét az x tengely körül. Az így kapott forgástest
térfogata: 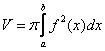
Forgástest palástterületének kiszámítása:
Legyen az f függvény (![]() ) folytonos és integrálható az
) folytonos és integrálható az ![]() intervallumon.
Forgassuk meg a függvény görbéjét az x tengely körül. Az így kapott forgástest
palástjának területe:
intervallumon.
Forgassuk meg a függvény görbéjét az x tengely körül. Az így kapott forgástest
palástjának területe: 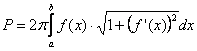 ;
;
Paraméteresen adott
függvény esetén: 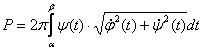
Szektorterület kiszámítása: Legyen az r polárkoordinátákkal megadott függvény
(![]() ) folytonos és integrálható az
) folytonos és integrálható az ![]() intervallumon. Legyen
intervallumon. Legyen ![]() és
és ![]() , O pedig az origó. Ekkor ABO
szektor területe:
, O pedig az origó. Ekkor ABO
szektor területe: 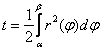
:
3832