Lézeres távolságmérés

mérési útmutató

Háromdimenziós látórendszerek működése

Általános alapelvek

Az ipar gyors fejlődése olyan módszerek kifejlesztését kívánja meg, amelyek kellőképpen rugalmasak, képesek alkalmazkodni a változó körülményekhez, igényekhez. Ez a követelmény csak úgy teljesíthető, ha a folyamatokat irányító rendszerek elegendő információt tudnak szerezni a környezetükből. Az ember, bár igen sokféle érzékszervvel rendelkezik a külvilágot leíró ismereteinek 90%-át a látás útján szerzi; és egyre inkább kitűnik, hogy a műszaki alkalmazások sem tudják nélkülözni az információszerzésnek ezt a formáját.

Besl [2] szerint, egy mesterséges látórendszer kellő rugalmasságához, hogy különböző problémák megoldásához ugyanazokat az eszközöket használhassuk, a rendelkezésre álló adatok feldolgozását - különösen a kezdeti lépéseket - a lehető legkevesebb speciális, az adott feladatra jellemző, a priori ismeret felhasználásával kell elvégezni (ez az úgynevezett adatvezérelt feldolgozás, data driven processing). Ezek az adatok szolgálnak bemenetül a feldolgozás azon részéhez, amely felhasználja a környezetről és a feladatról rendelkezésre álló információkat (ez a modellvezérelt feldolgozás, model driven processing).

Az első mesterséges látórendszerek az emberi szem által is érzékelt látványból, a klasszikus fényképezési eljárások útján készült képekből indultak ki. Ezek az úgynevezett intenzitásképek (intensity image), melyek képek a szó köznapi értelmében; azaz az egyes pontok fényessége attól függ, hogy a környezet adott pontnak megfelelő helyéről az érzékelőbe mennyi fény jut. Az intenzitáskép a tárgyat megvilágító fénynek az érzékelőbe való visszaverődéséből alakul ki. Mind a fényforrás, mind az érzékelő modellezése igen bonyolult feladat, az objektumról pedig általános esetben semmilyen információ nem áll rendelkezésünkre, ezért intenzitáskép alapján nehéz feladat a látott objektumok alakját, térbeli elhelyezkedését meghatározni 636i84g , és az adatok általában nem értelmezhetők egyértelműen.

Egyre szélesebb körben alkalmaznak ezért olyan eszközöket, amelyek közvetlenül alkalmasak távolság mérésére. Ezek a vizsgált térrészről úgynevezett távolságképet (range image, depth map) készítenek, melynek pontmátrixában távolságmérések eredményei szerepelnek (például a kép (x1,y1) koordinátájú pontjának értéke: az objektum magassága - azaz az xy síktól való távolsága - az (x1,y1) pontban). A távolságkép azonban igen sok - általános célú módszerek kidolgozásához nélkülözhetetlen - információt nem tartalmaz az objektumról (pl. felületének mintázata, anyagi minősége), és a képek bizonyos kedvezőtlen tulajdonságai (pl. nem abszolút integrálható) megnehezítik a feldolgozásukat.

Az intenzitás- és távolságkép közötti kapcsolat

Egy térbeli felület ideális esetben, (x, y, z) Descartes koordináta rendszerben matematikailag egy, az (x, y) síkbeli tartományon értelmezett  alakú egyenlettel írható le.

Az ideális távolságkép (x,y) koordinátájú pontjának az értéke ebben az esetben z (tehát a távolságkép az f függvény mintáit tartalmazza). A z=f(x,y) távolságfüggvényt matematikailag vizsgálva: az értelmezési tartománya az alkalmazott felvételi módszertől függően az xy sík nem biztosan egyszeresen összefüggő tartománya (lehet, hogy egyes pontokról nem tudunk információt szerezni), az értékkészlete pedig nem véges (a távolság értéke végtelen is lehet). A függvény így nem abszolút integrálható, ezért nem Fourier-transzformálható, ezen alapuló feldolgozási módszerek csak korlátozottan alkalmazhatóak.

Ebből az ideális távolságkép alapján meghatározható az ideális intenzitáskép, a megvilágítás és a reflexiós modell megadásával. A Lambert-féle reflexiós modell szerint:

Ahol I itt a pont fényessége, r a visszaverődési tényező (a felület anyagi minőségétől, szerkezetétől és a fény hullámhosszától függő), n a felületi egységnormális, s a megvilágítás irányvektora.

A normálvektor az f felületre:

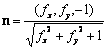
így:

Ha r és s állandó, akkor az (x,y) pontban az intenzitás az f függvény (lényegében a távolságkép) x és y koordináták szerinti parciális deriváltjaival arányos. Az ideális intenzitáskép (x,y) koordinátájú pontjának az értéke tehát:

Távolságképek készítése

Távolságképek készítésére sok módszer ismert, ezeket az alábbi ábrán foglaltuk össze ([6] alapján).

A passzív technikákban olyan képekkel dolgozunk, amelyek a vizsgált területet megvilágító (természetes vagy mesterséges) fények visszaverődéséből alakulnak ki. Általában több ilyen kép alapján határozunk meg mélységi információt (térben, időben felvett képsorozatból), vagy az intenzitásképből kinyerhető más jellemzőkből (árnyékolás, kontúr stb.). [10]

Az aktív technikák esetén meghatározott jellel tapogatjuk le a vizsgált területet, leggyakrabban ultrahanggal vagy lézerrel. Ezek a módszerek általában megbízhatóbb távolságadatokat szolgáltatnak, mint a passzív technikák.

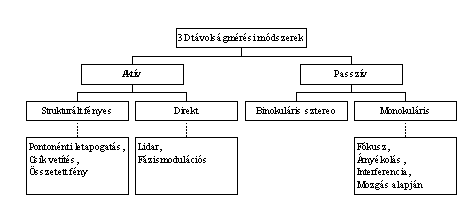
Távolság mérésére használt módszerek mesterséges látórendszerekben

A trianguláció elvét alkalmazó strukturált fényes módszer egyes változatait ismertetjük és hasonlítjuk össze a következő részben ([5] szerinti osztályozást követve).

Pontonkénti lézer letapogatás

A trianguláció elvén alapuló legegyszerűbb távolságérzékelő érzékelő vázlatos felépítése látható az alábbi ábrán. Lézersugárral megvilágítjuk a vizsgált felület egy pontját, az onnan visszaverődő fényt egy gyűjtőlencsével a pozícióérzékelőre fókuszáljuk. Annak alapján, hogy a pozícióérzékelő mely pontjára jut fény, a visszaverődés helye megállapítható.

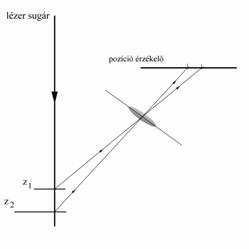
Pontonkénti lézer letapogatás modellje

Fénykés

A pontonkénti letapogatás módosított változata, pontszerű megvilágítás helyett az objektumra egy csíkot vetítünk, ahogy az alábbi ábrán látható. A csík előállítható gyorsan mozgó lézerpont segítségével, vagy egyéb fényforrás alkalmazásával. Egy felvételből a csík összes pontjának térbeli koordinátái meghatározhatóak, és ez a pontonkénti letapogatásnál nagyobb sebességet tesz lehetővé, a számítási idő növekedése árán.

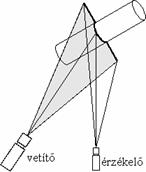
Fénykéses megvilágítás

Összetett fény

A vizsgált területre egy időben több csíkot vetítünk, és ezzel egy lépésben az egész térrészről információt kapunk.

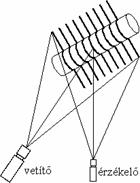
Összetett fényes megvilágítás

A módszer hátránya azonban, hogy az adatok kiértékelése nem minden esetben vezet egyértelmű eredményhez, mint ahogy az az alábbi ábrán látható lépcsős felületnél megfigyelhető. A csíkok ugyanis az ugrás jellegű éleknél eltűnnek, majd a következő látható felületrészen bizonyos eltolással ismét megjelennek. Az eltolás mértéke a felület ismerete nélkül nem számítható ki, ezért a csíkok összekeveredhetnek, végigkövetésük nem lehetséges, a távolságmérés nem végezhető el.

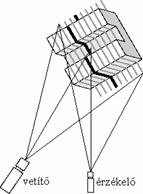
Egyszerre több csíkot vetítve az egyes csíkok menete nem minden esetben követhető végig egyértelműen

Kódolt fény, és módosított változatai

Az előző pontban bemutatott módszernél leírt többértelműség kiküszöbölésére fejlesztették ki ezt az eljárást. A vizsgált felületre itt is egyszerre több csíkot vetítünk, de a területről több felvétel is készül és az egyes felvételeken az összes csík közül csak egyeseket jelenítünk meg, bizonyos kódolás szerint. Minden csíknak egyedi sötét/világos sorozat felel meg, így ezek egymástól egyértelműen elkülöníthetők.

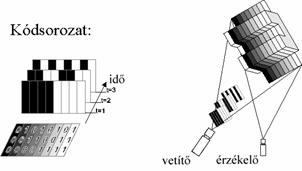
Kódolt fény: az egyes csíkokat bizonyos kódolás szerint világítjuk meg

Lehetséges kódolás különböző színek illetve szürkeárnyalatok alkalmazásával (színkódolás), ezek a módszerek azonban igen érzékenyek a felületek minőségének, színének változásaira, a környezetből származó fényhatásokra, ezért csak speciális esetekben használhatóak.

Ha a csíkok intenzitásának változása koszinusz jellegű függvényt követ, és a függvény fázisát időben folyamatosan módosítjuk, akkor az ilyen módon megvilágított felületről készült néhány felvétel alapján, egyszerű számításokkal nyerhetünk igen pontos információkat a vizsgált felületről. Azonban többértelműségi problémák ennél a módszernél is felléphetnek, ezért abszolút távolság mérésére csak korlátozottan használható.

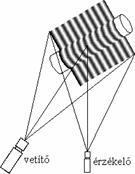
A csíkok intenzitásának változása koszinuszos függvényt követ

Alkalmazzák ez előbbi módszerek kombinációit is:

Színkódolt fázistolás: egyszerre vetítünk fel háromféle, fázisában eltolt intenzitás-eloszlást, különböző színekkel, így egy felvételből meghatározhatjuk a térbeli információkat; a módszer előnye, hogy nagyon gyors, így mozgó tárgyak esetén is alkalmazható

Fázistolás és kódolt fény kombinációja: a többértelműségek kiszűrhetők és a kódolt fény módszernél pontosabb eredményekhez jutunk.

A módszerek összehasonlítása

Az előző pontokban leírt módszerek jellemzőit az alábbi táblázatban foglalhatjuk össze ([5]):

Az alkalmazott eszközök és módszerek ismertetése

A mérőrendszer felépítése és működése

A mérőrendszer szinkronizált triangulációt alkalmaz, ahol a szinkronizáció azt jelenti, hogy az érzékelő geometriai helyzetét a letapogató lézersugár mozgatásával szinkronban változtatjuk. Így a mérőrendszerhez a detektált fénysugár eltérítő mechanizmusa is hozzátartozik.

A mérőrendszer felépítését az alábbi ábrán mutatjuk be. Az 5mW-os HeNe lézerforrásból (1) a fény a kétoldalas x irányú eltérítő tükörre (2), majd a (3) állótükrön megtörve a (4) y irányú eltérítő tükörre jut. A lézerfénnyel megvilágított tárgyponton szétszóródó fény egy része az (5), (6) és (2) tükrökön keresztül a gyűjtőlencsébe (7) jut. A lencse a fényt a CCD érzékelőre (9) fókuszálja. Az eltérítő tükröket a (10), (11), (12) galvánmotoros eltérítő egységek mozgatják.

Az x irányú szinkronizációt a kétoldalas tükör (2) automatikusan biztosítja. Az y irányú szinkronizációt a (4) és (5) eltérítő tükrök mozgatásának szinkronizálásával oldjuk meg. Így ez a szinkron nem automatikus, és nem is tökéletes (Egydimenziós CCD vonalérzékelő alkalmazása esetén ezért hengerlencse (8) elhelyezése szükésges, amely a gyűjtőlencséről érkező fényt az érzékelési szakaszra merőleges fénycsíkba fókuszálja.)

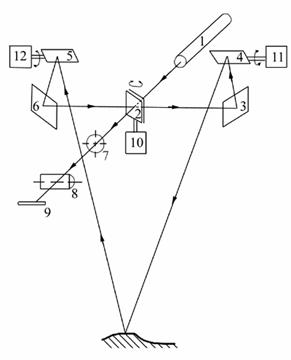
A mérőrendszer felépítése

A szinkronizált pontonkénti lézer letapogatás geometriája

A kétdimenziós geometriai modell

Az alábbi ábrán látható elrendezésben az x tengely (d; 0) pontjából vetítjük a letapogató lézersugarat. A koordinátarendszer origójában helyezkedik el a kamera gyűjtőlencséjének geometriai középpontja. Célunk, hogy a detektor egyenesére illesztett P tengelyen meghatározzuk a lézerfény által megvilágított tárgypont képpontjának helyét. A P tengely 0 pontja a P tengely és a lencse geometriai tengelyének metszéspontjában van. Az egyszerűbb geometriai leírást segíti, hogy a detektor egyenesét az xz síkban az origó körül elforgatjuk (Q -kal (szinkronizáció), így a P tengely mindig párhuzamos lesz az x tengellyel, tőle való távolsága pedig

(1)

ahol f a gyűjtőlencse fókusztávolsága és l a tárgytávolság.

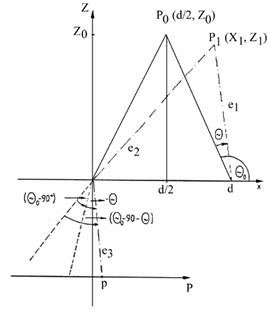
A szinkron trianguláció geometriai modellje 2 dimenzióban

Elemi koordinátageometriai megfontolások alapján, a levezetés mellőzésével a képpont helye a detektor egyenesén:

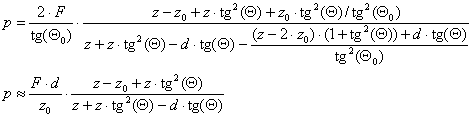(2, 3)

Ebből p-nek z-re illetve Dx-re vonatkozó érzékenysége:

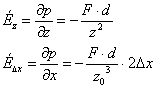(4, 5)

Fenti két kifejezés összevetéséből látható, hogy p-nek z-re való érzékenysége jóval nagyobb, mint Dx-re. Ezt konkrét példával szemléltetjük az alábbi ábrán (z = 750 mm, d = 150 mm, f = 200 mm; ábrázoltuk p(Dz) függvényt Q és p(Dx) függvényt z=z₀ feltétel mellett).

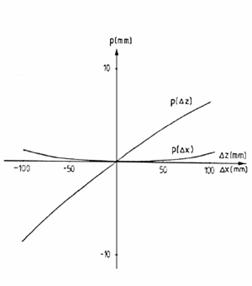
A képpont helyzete a vonalérzékelőn (p) a távolság (Dz) és az oldalirányú eltérítés (Dx) függvényében

A háromdimenziós geometriai modell

Az x tengelytől h távolságra helyezkedik el a lézersugár y irányú eltérítését és a detektált fénysugár visszatérítését biztosító síktükör H forgástengelye. Ezzel az y irányú szinkronizált eltérítéssel biztosítjuk, hogy a detektált fénysugár mindig visszatér az xz síkba. Az alábbi ábra szerint a P(x,y,z) és az xz síkban lévő P'(x,y,z') pontoknak megfelelő p koordináta megegyezik. P' ponthoz úgy jutunk, hogy az APB háromszöget H tengely körül az xz síkba beforgatjuk. Ekkor z és z' között a következő összefüggés áll fenn:

(6)

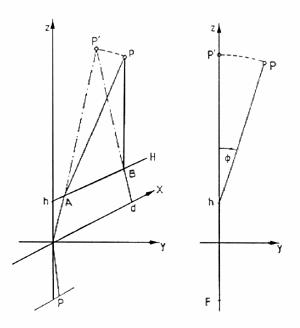
A trianguláció geometriai modellje három dimenzióban

A (2) egyenlet szerint P mérési eredmény ismeretében z' egyértelműen meghatározható. Ennek ismeretében P(x,y,z) pont koordinátáit a következő összefüggések adják:

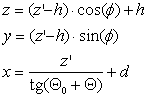(7, 8, 9)

A fentiek alapján a szinkronizált triangulációs mérési elv alkalmazásának fő jellemzői:

Az x irányú szinkronizált eltérítés következtében a detektált fénypont pozíciója lényegében csak a vizsgált tárgypont távolságának, z koordinátájának a függvénye. Ezért nagy mélységi felbontóképesség és nagy x irányú látószög érhető el.

Az y irányú szinkronizáció a három dimenziós mérést valójában két dimenziós mérési feladattá transzformálja. Ez lehetővé teszi, hogy detektorként vonalérzékelőt alkalmazzunk és, hogy y irányban is nagy látószöget érjünk el.

A rendszer korlátai

Előfordul, hogy adott pontot megvilágítva az érzékelőbe nem jut a környezeti fénynél számottevően több energia: ilyen esetben nem tudunk távolságot mérni. Ennek okai a következők lehetnek:

a fénysugár áthalad vagy elnyelődik a felületen (átlátszó, illetve erősen elnyelő vagy egyenetlen felületű tárgyakon), a felületről visszaverődő fény intenzitása erősen lecsökken (a)

a tárgy felületén direkt reflexió történik, a beeső fénysugár jól meghatározott irányba verődik vissza, a szóródás mértéke csekély, így az érzékelő látószögébe eső térrészből nem érkezik számottevő mennyiségű fény (b)

a fénysugár közel párhuzamos a tárgy felületével, így a lézerpont véges kiterjedése miatt szélesebb mélységtartományból történik meg a visszaverődés és ez a vonalérzékelőn lapos, elnyújtott csúcsként jelenik meg, amely nem különíthető el a környezetből származó zavaró fények által okozott intenzitásváltozásoktól (c)

árnyékolási jelenség: mivel az érzékelő és a fényforrás nem egy pontban vannak, a tárgy leárnyékolhatja a megvilágított pontból szétszóródó fénynek az érzékelő látószögébe eső részét (d)

a tárgy felülete olyan mértékben elnyeli a megvilágító fény energiáját, hogy a visszaverődő fény nem különíthető el a környezetből érkező egyéb fényektől

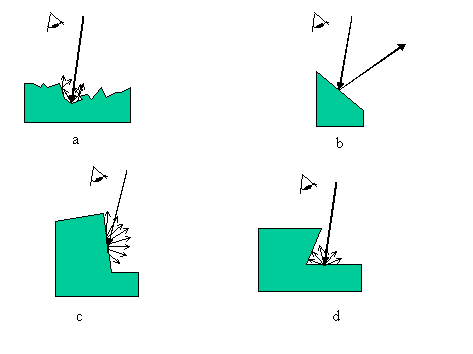
Bizonyos esetekben az érzékelőbe nem érkezik megfelelő intenzitású visszavert fény (a. többszörös visszaverődés, b. direkt reflexió, c. nagy beesési szög, d. árnyékolási jelenség)

A tárgy felületi minőségéből adódó problémák a lézersugár energiájának növelésével, az érzékelőre érkező fény szűrésével, illetve a felület megváltoztatásával (a felület bevonása, mechanikai megmunkálás) enyhíthetők.

A nagy beesési szög miatt fellépő hatás intenzitáscsökkenés mérsékelhető koncentráltabb fénynyaláb alkalmazásával.

Az árnyékolás jelensége a mérés elvéből adódik, csak akkor nyerhetünk maradéktalan leírást a tárgyról, ha azt mozgatjuk, különböző nézőpontokból vizsgáljuk (például dönthető, forgatható alapra helyezzük el; ha a mozgatás paraméterei rendelkezésre állnak, rekonstruálható az árnyékmentes látvány).

A berendezés beállítása és kalibrációja

A berendezés beállítása során biztosítanunk kell:

a két y irányú eltérítő tükör egytengelyűségét

az y irányú eltérítő tükrök és a CCD vonalérzékelő párhuzamosságát

a lézerfény, az y irányú eltérítő tükrök és a CCD vonalérzékelő egysíkúságát

az x irányú eltérítő tükör tengelyének merőlegességét a lézerfény és az y irányú eltérítő tükrök tengelyére

A berendezés kalibrációja:

z0 távolságra elhelyezünk egy z-tengelyre merőleges referencia síkot, amelynek segítségével elvégezzük az x és y irányú eltérítés kalibrációját

beállítjuk a két y irányú eltérítő tükör együttmozgását, szinkronizációját

elvégezzük a referencia síkhoz viszonyított mélységi (z irányú) kalibrációt, úgy, hogy a z₀ távolságban elhelyezett referencia síkra ismert vastagságú mérőhasábokat helyezünk, és felvesszük a p(Q_i,z_i)

A mérőrendszer megvalósítása

Távolságkép felvételéhez a tükröket mozgatva végig kell pásztázzuk a tárgyfelület pontjait, mindenütt megmérve a lézerpont helyét a CCD érzékelőn. Ehhez a feladathoz egy PC-t használunk, mely a jelfeldolgozó processzorral felszerelt kamerával egy szabványos RS-232 soros vonalon kommunikál, a tükröket pedig egy egyszerű DA átalakító segítségével állítja. A mérési adatokat Matlab program segítségével értelmezzük, elemezzük és jelenítjük meg.

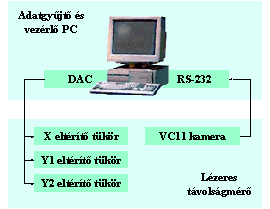
A mérőrendszer megvalósításának blokkvázlata

Kamera és jelfeldolgozó

A tárgyfelületről visszaverődő fényt a Vision Components cég VC11 típusjelű kamerájával detektáljuk, melyet kifejezetten valós-idejű képfeldolgozási feladatokhoz fejlesztettek ki. Ehhez a kamerában egy nagy teljesítményű, jelfeldolgozó processzor (DSP - Digital Signal Processor) alapú számítóművet valósítottak meg.

A kamerában markerkövető algoritmust futtatunk (a marker valamilyen jellegzetes, a képen könnyen felismerhető objektum - esetünkben a lézersugár fényes beesési pontja). A marker súlypontjának aktuális pozícióját a kamera a soros portján keresztül folyamatosan szolgáltatja.

A kamera működését alábbi ábrán látható blokkvázlata alapján mutatjuk be.

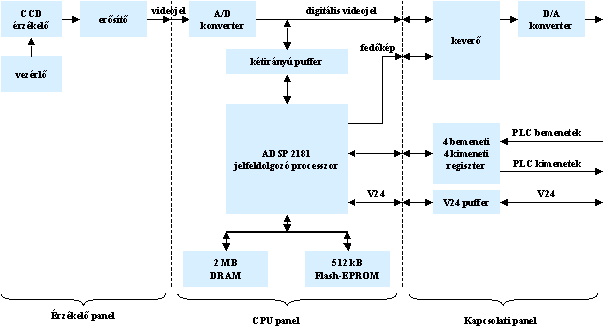
Vision Components VC11 videokamera blokkvázlata

A kamera három egységből épül fel az érzékelő, a CPU és a kapcsolati panelből.

Az érzékelő panel rögzíti a képet egy ICX059AL típusjelű CCD érzékelő segítségével. A készült kép mérete 752x582 képpont.

A panelből kimenő analóg jelet a CPU panel használja fel. A CPU panelen az Analog Devices cég ADSP2181 típusjelű jelfeldolgozó processzora működik (80 kB belső RAM-mal, 2MB külső DRAM, 512kB külső Flash-EPROM memóriával). A videojel digitalizálás után a processzor által elérhető DRAM-ba kerül. A panel digitális videojel kimenetére akár közvetlenül az A/D átalakítóról érkező jel, akár egy DRAM-ban lévő kép továbbítható. Emellett egy bináris (1 bit színmélységű fekete-fehér) kép helyezhető a megjelenített képre, ennek videojelét közvetlenül a processzor állítja elő (ez a módszer alkalmas pl. különféle grafikák, feliratok, kurzorok élő képre való vetítésére). A processzor 4 kimeneti és 4 bemeneti digitális vonalat kezel különféle egyszerűbb vezérlési feladatok támogatására. A kamera V24 (RS232) szabványú soros vonalon keresztül is kommunikál a külvilággal (maximum 115200 baud sebességgel).

A kapcsolati panel elvégzi a fedőkép ráhelyezését a videoképre, és az így kapott videojelet D/A átalakítás után külső csatlakozóra vezeti ki. A panel a processzor által kezelt TTL/CMOS szintű jeleket galvanikusan leválasztja és 12/24V-os PLC jelekhez illeszti. Ezen kívül a panel a V24 vonal pufferelését és jelszint illesztését is végzi.

A kamerán VC/RT valós-idejű operációs rendszer fut, amely a felhasználó által írt programok futtatását, képek rögzítését és megjelenítését, valamint a soros interfészen keresztüli kommunikációt végzi.

A kamerához a mellékelt GNU C fordítóval készíthetünk saját programokat. Képfeldolgozó algoritmusok megvalósítását az igen gazdag VCLIB nevű optimalizált függvénykönyvtár segíti.

A kamera nagyon jól használható a legkülönbözőbb képfeldolgozási feladatokra, ugyanis a műveletek legjelentősebb része "helyben", a jelfeldolgozó processzor által elvégezhető, és ez igen gyors, pontos és megbízható működést eredményez.

Technikai jellemzők

Sugárforrás: 5 mW teljesítményű HeNe lézercső

CCD kamera:

Vision Components VC11 (CCD kamera+ADSP 2181 processzor)

752x582 felbontás

256 szürkeárnyalat

Tükörmozgató elektronika:

Emalog gyártmányú galvanomotorok

0..5V alapjel, PID szabályozó

A triangulációs rendszer adatai:

névleges mérési távolság (z₀) 750 mm

bázistávolság (d) 200 mm

Látómező:

x irányú: eltérítési szög mellett 100 mm;

y irányú: eltérítési szög mellett 150 mm;

vizsgálható mélységi tartomány: 750 100 mm

Felbontóképesség:

z irányú: 0,5 mm

x irányú: 0,1 mm

Mérés menete

Beugró

A mérésre az útmutató alapján előzetesen fel kell készülni! Ezt a mérés elején ellenőrizzük, és ennek eredménye beleszámít a kapott osztályzatba.

Tudni kell a következőket:

A mérés elve az útmutató alapján: az intenzitás- és távolságkép közötti kapcsolat, távolságképek készítése, a mérőrendszer megvalósításának értése, a szinkronizált pontonkénti lézer letapogatás geometriájának elve, a rendszer korlátai

C programozás alapjai

Matlab alapvető funkcióinak ismerete, valamint function; fopen, fscanf, fclose; polyfit, polyval; image, colormap, mesh, surf  használata.

Mérési feladat

Bármilyen számítógépen a felvett képek a C:\MERES\3DSCAN\ÉÉHHNN könyvtárban dolgozzon (ÉÉHHNN a mérés dátuma). Ezen belül a mérésvezérlő forráskódját a SRC, a Matlab függvényeket a MATLAB, a kész mérési adatokat a RAW könyvtárba mentse.

Készítse el a PC-n futó vezérlő és adatgyűjtő programot (kiindulásként használja a függelékben található programvázlatot), mely a következő funkciókat tudja ellátni:

A.     Az X és Y1, Y2 eltérítő tükröket a kurzormozgató gombokkal irányítja

B.     Az eltérítő tükrök mozgatásával kirajzol a lézerrel egy megadható méretű téglalap alakú területet (a letapogatandó terület kijelölésére)

C.     Megadható méretű és sűrűségű pontrács szerint távolságérték mintát vesz (letapogatja a tárgyfelületet), és a mérési adatokat Matlab számára értelmezhető formájú szöveges fájlba helyezi (.raw kiterjesztés, ld. példa a függelékben; ügyeljen a helyes tükörmozgatási stratégia megválasztására, és a marker pozíció mérhetetlenség kezelésére)

Ellenőrizze a távolságmérő kalibrációját és a PC-n futó program helyes működését!

A.     Készítsen néhány felvételt a tükrök teljes mozgási tartományában néhány az alapsíkkal párhuzamos síkról

B.     Elemezze az elkészült szövegfájlok alapján a felvételeken látható eltéréseket az ideális eredményektől (használható terület behatároltsága, ennek oka, zaj, nemlinearitások; a jegyzőkönyvben egy konkrét képen ezek bemutatása)

C.     A felvételek alapján határozza meg a távolságmérésre elfogadható pontossággal használható területet, szükség szerint a mérőrendszer elemeinek kis mértékű elmozdításával korrigálja az észlelt rendellenességeket. A továbbiakban ezen a területen belül dolgozzon!

Jelenítse meg Matlab programmal a távolságképeket

A.     Vegye fel egy lépcsős elrendezés (stairs.raw) és néhány tetszőleges forma távolságképét

B.     Írjon Matlab függvényt (draw1(img)), amely síkbeli szürkeárnyalatos képként jelenít meg egy tetszőleges távolságképet (img egy egyszerű mátrix, mely a raw fájlból a rawread(filename) függvénnyel nyerhető)

Kézfej távolságképének síkbeli szürkeárnyalatos ábrázolása

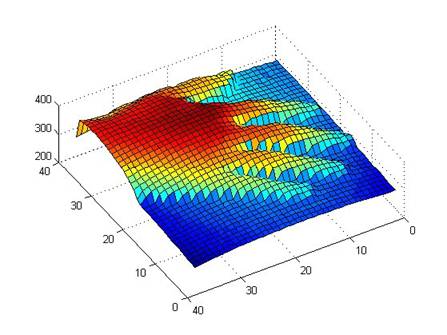
C.     Írjon Matlab függvényt (draw2(img)), amely térbeli felületként jelenít meg egy tetszőleges távolságképet (ilyen kép ld. a címlapon)

D.     Írjon Matlab függvényt (draw3(img, linecount)), amely szintvonalas ábrázolással jelenít meg egy tetszőleges távolságképet (megadható legyen, hogy hány vonallal ossza fel a teljes távolságtartományt)

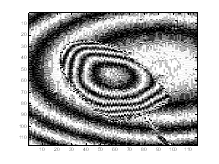
Egy egér (a számítógépes pozícionáló eszköz) távolságképének szintvonalas ábrázolása

E.      Nézze meg a távolságképeket a megvalósított függvényekkel! Készítsen símítószűrőket a különféle hibák zavaró hatásának csökkentésére (pl. medián szűrő: filtmed(img,winsize), csak a mérhetetlen pontokban alkalmazott medián szűrő: filtmed2(img,winsize), aluláteresztő konvolúciós szűrő: filtconv(img)), és hasonlítsa össze az eredményt az előző képekkel

Kalibrálja a marker pozíció mérésének adatait

A.     Vegye fel 10 db egymástól 1 cm-re lévő sík távolságképét (kb. 15x15-ös felbontással, fájlnevek: calib00.raw, calib01.raw, . calib09.raw)

B.     A síkok középpontjában mért adatok alapján állapítsa meg a pozícióadat és a valódi távolság közötti függvénykapcsolat jellegét

C.     Milyen a függvénykapcsolat a síkok széleinek közelében? Mi ennek az oka?

D.     Adjon becslést a mérőrendszer pontosságára. Hogyan változik a hiba a teljes mérési tartományban?

Mérési jegyzőkönyv

A mérésről mérőcsoportonként egy jegyzőkönyvet kell készíteni. A kapott osztályzat a beugró eredményéből és a jegyzőkönyvből alakul ki.

A mérési jegyzőkönyvben szerepeljen:

a vezérlő és adatgyűjtő program és minden Matlab függvény forráskódja

a szöveges elemzéseket támassza alá megfelelő szemléletes kép beillesztésével

A mérés végeztével ellenőrizze, hogy a szükséges forrásfájlok és mérési eredmények megtalálhatók a megfelelő könyvtárakban.

Függelék

Vázlat PC-n futó mérésvezérlő és adatgyűjtő programhoz

* 3dscan.cpp

*

* MoMic

*

* Written by: evf., szak, merocsoportszam

* Date: yyyy.mm.dd

*/

#include <stdio.h>

#include <string.h>

#include <stdlib.h>

#include <conio.h>

#include <math.h>

#include <dos.h>

#include <process.h>

#include "camera.h"

#include "mirror.h"

int MirrorMove(void)

int ShowField(int x1, int x2, int y1, int y2)

int ScanField(char* fn, int x1, int x2, int nx, int y1, int y2, int ny)

void Instructions()

int main(int argc, char *argv[])

CameraInit();

MirrorInit();

if (!strcmp(argv[1],"move"))

result=MirrorMove();

else if (!strcmp(argv[1],"field"))

else if (!strcmp(argv[1],"scan"))

else

Instructions();

CameraDone();

MirrorDone();

return result;

Tükörmozgató és kamerakezelő rutinok (deklarációk a mirror.h, camera.h fájlokban)

const int MIRROR_MIN=0;                // x, y1, y2 tukor DAC minimum ertek (0V)

const int MIRROR_MAX=4095;             // x, y1, y2 tukor DAC maximum ertek (+5V)

const int MIRROR_ORG=2048;             // x, y1, y2 tukor kozepallasanak megfelelo DAC ertek

void SetMirrorX(int dax);              // X tukor mozgatasa a DAC ertek megadasaval

void SetMirrorY(int day1, int day2);   // Y1, Y2 tukor mozgatasa a DAC ertekek megadasaval

int CameraGetCoords(int *x, int *y);   // Marker pozicio lekerese a kamerabol

// visszateresi ertek hiba eseten (nem talalt markert) -1

Távolságkép példa (fullscan.raw)

Az első két sor fejléc:

minimális és maximális DAC érték, minták száma az X tengelyre (1. sor)

minimális és maximális DAC érték, minták száma az Y tengelyre (2. sor)

Ezután következnek a nyers mérési adatok (marker pozíció X koordinátája), egymástól szóközzel elválasztva, sor végén CR/LF-el lezárva.

Matlab programvázlatok

%Read raw file in matrix

function img=rawread(filename)

fid=fopen(filename)

a=fscanf(fid,'%f %f %i',3);

xmin=a(1)

xmax=a(2)

xno=a(3)

a=fscanf(fid,'%f %f %i',3);

ymin=a(1)

ymax=a(2)

yno=a(3)

img=fscanf(fid,'%i',[xno,yno]);

fclose(fid)

Irodalomjegyzék

Besl, P. J., Jain, R.C. [1986]. Invariant surface characteristics for three-dimensional object recognition in range images. Computer Vision, Graphics, Image Processing, 33, (Jan.), 33-80

Besl, P.J. [1988]. Surfaces in Range Image Understanding, Springer-Verlag, Springer Series in Perception Engineering

Gil, B., Mitchie, A., Aggarwal, J.K. [1983]. Experiments in combining intensity and range edge maps. Computer Vision, Graphics, Image Processing, 21, (Mar.), 395-411

Haralick, R.M., Watson, L.T., Laffey, T.J. [1983]. The topographical primal sketch. Int. J. Robotics Res. 2, 1 (Spring) 50-72

Jais, S.[1997]. Investigations on Optical 3D Measurement Techniques and Implementation of an Optical Range Sensor, diplomamunka, Johannes Kepler Universität, Linz

Sanz, J.L.C. [1989]. Advances in Machine Vision, Springer-Verlag, New York

Wager, R. [1992]. Integrierte Auswertung von Abstands- und Intensitätsbildern, diplomamunka, Universität Karlsruhe

Wei, J. [1989]. Modellgesteurte Szenen-Interpretation durch Fusion von Intensitäts- und Abstandbildern, doktori disszertáció, Universität Karlsruhe

Lassó, A. [1998]. Háromdimenziós képek feldolgozása és illesztése CAD adatbázishoz, TDK dolgozat, Budapesti Műszaki Egyetem

Fisher R. B. [2000] CVOnline https://www.dai.ed.ac.uk/CVonline/