F I Z I K A I.

KOLLOKVIUMI TÉTELEK

1. A hosszúság és idő mérése.

Meas_length_time.pdf !

2. Pálya, út, elmozdulás, sebesség, gyorsulás fogalma. Az egyenesvonalú egyenletes és az egyenesvonalú egyenletesen változó mozgás (szabadesés).

A szabadesés I

A szabadon eső tárgy mozgása egyenesvonalú, egyenletesen gyorsuló mozgás. A test gyorsulása az ún. gravitációs, vagy nehézségi gyorsulás, iránya mindig lefele mutató, értéke g=9,81 m/s². A szabadesésre vonatkozó alapösszefüggéseket az a=g behelyettesítéssel az egyenesvonalú egyenletesen gyorsuló mozgás alaptörvényeiből kapjuk.

A mozgás

A mozgás megértése kulcsfontosságú kérdés a fizikában, a leírásához viszont bonyolultsága miatt bizonyos megszorításokkal, egyszerűsítésekkel kell élnünk. Az emberi járástól az anyagi pont egyenesvonalú mozgásáig az út hosszú és rögös. Az ember járás közben a végtagjait mozgatja, lépésről lépésre halad előre. Nehézségeink támadnának, ha az ember járását szeretnénk matematikai módszerekkel leírni - nem lehetetlen, de egy számítógép kapacitása szükségeltetik hozzá. Elődeinknek nem álltak rendelkezésére szimulációs rendszerek, így a jelenségek leírásához a fizikai valóság egyszerűsített modelljeit kellett használniuk. Így definiálták a szilárd testet mint fizikai fogalmat. A szilárd test egy olyan test, amelyik mozgás közben nem változtatja a formáját (ez egy egyszerű példa arra, hogy miként lehet megszabadulni a zavaró körülményektől, és hogyan lehet egyszerűsíteni a fizikai leíró modellt)

A történet itt nem ér véget, még mindig előttünk áll a mozgások sokfélesége. Egy elhajított kő görbevonalú pályát ír le a levegőben. Egy elejtett labda gurul a talajon, halad is meg forog is egyidőben, sőt ugrik is néhányat a lépcsőkön. Tornászok, műkorcsolyázók meglepő dolgokat képesek bemutatni, néha azt hisszük, hogy felette állnak a fizika törvényeinek (pedig nem). Hogyan lehet bonyolult mozgásokat egyszerű összetevőkre bontani? A mozgást tanulmányozó gondolkodóink rájöttek arra, hogy a testeknek van egy jellemző pontjuk, amelyik a test bonyolult mozgása ellenére igen egyszerűen viselkedik, mozgása pedig jellemzi a test egészének mozgását. Ezt a pontot a tömegközéppontnak nevezték el. Önként kínálkozik a kérdés, hogy hol van a tömegközéppont? A tömegközéppont a testek egyensúlyi pontja, meghatározására számtalan módszer létezik. Ha egy testet a tömegközéppontjában alátámasztunk, akkor egyensúlyban marad. Ez az eljárás nem mindig vezet eredményre, mert a legtöbb esetben a tömegközéppont a test belsejében van. Másrészt, ha egy testet bármelyik pontjában felfüggesztünk, akkor elfordul, éspedig úgy, hogy a tömegközéppontja pontosan a felfüggesztési pont alá kerül. Két felfüggesztéssel már meghatározhatjuk egy test tömegközéppontjának helyzetét úgy, hogy a felfüggesztési pontból függőleges vonalakat húzunk - a test tömegközéppontja két vonal metszéspontjában lesz.

Miért ennyire fontos a tömegközéppont? Azért, mert a szilárd testek mozgása - bármilyen bonyolult is legyen az - a tömegközéppont elmozdulására és a szilárd test tömegközéppont (esetenként más tetszőleges pont) körüli forgására vezethető vissza. Most már csak egy pont mozgását és egy testnek egy pont körüli forgását kell tanulmányoznunk, és ez a feladat sokkal, de sokkal egyszerűbbnek tűnik, mint az általunk észlelt mozgások többsége, és higgyétek el, az is.

3. Körmozgás. Harmonikus rezgőmozgás.

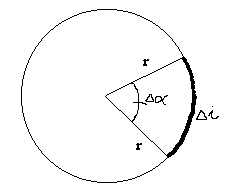
Körmozgást végez egy tömegpont akkor, ha a megtett út a körpályán befutott ív.

A körmozgás jól jellemezhető a mozgó ponthoz húzott sugár elfordulásának szögével, amelyet radiánban mérünk.

Ekkor a befutott ív hosszúsága és a  szögelfordulás között a következő egyszerű összefüggés érvényes:

= r *

A időre vonatkozó átlagos kerületi sebesség a  idő alatt befutott ívhossz és a megtételéhez szükséges idő hányadosa:

Ha a elegendően kicsiny, akkor v a pillanatnyi kerületi sebesség.

Helyettesítsük a  ívhosszat a sugárral és a hozzátartozó kis szögelfordulással:

A  hányados a szögsebesség.

Jele: , dimenziója: 1/ idő, mértékegysége

Képlettel kifejezve:

= ,

amivel a kerületi sebesség nagysága és a szögsebesség kapcsolatára a 939b16j

v = r *  összefüggés adódik.

! Mivel a körpályán mozgó test sebessége változik, ezért biztos, hogy van gyorsulása.

Definíció:

A körpályán mozgó test gyorsulásának normális komponense a centripetális (középpontba mutató), tangenciális gyorsulása a kerületi gyorsulás.

A kerületi gyorsulás a körmozgást végző test sebességének nagyságát változtatja, így a pillanatnyi sebesség és a kerületi gyorsulás kapcsolatát a

összefüggés adja.

A negatív előjelet akkor használjuk, ha a sebesség és az érintő irányú gyorsulás ellentétes irányú.

Az egyenletes körmozgás

Definíció:

Egyenletes körmozgásról beszélünk, ha a pálya kör, és a mozgó test által befutott ív arányos a befutáshoz szükséges idővel.

A definícióból következik, hogy a kerületi sebesség, a szögsebesség és a centripetális gyorsulás állandó, a kerületi gyorsulás pedig nulla.

Így a mozgást leíró összefüggések a következők:

Az egyenletes körmozgás leírásához még két mennyiséget definiálunk:

-         A körpálya egyszeri teljes befutásához szükséges időt keringési időnek nevezzük és T-vel jelöljük.

-         Az egységnyi idő alatt befutott körök száma a fordulatszám, jele: n.

A két definícióból következik, hogy e két mennyiség egymás reciproka:

A szögsebességet a keringési idővel és a fordulatszámmal kifejezve:

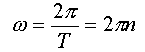
Az egyenletes körmozgás dinamikai feltétele:

(az egyenletes körmozgást végző testre ható erők eredője a kör középpontjába mutat, nagysága

)

! Az eredő erőt, amely a tömegpontot a körpályára kényszeríti, centripetális erőnek nevezzük.

A harmonikus rezgések - bevezetés

Környezetünkben a rezgéseknek számos példájával találkozhatunk. Legismertebb az ingamozgás, minden felfüggesztett tárgy ingaként leng az egyensúlyi állapota körül, ha abból kimozdítjuk. Ha egy hangszer húrját megpendítjük, a húr rezgésbe jön, és rezgésbe hozza a környező levegőt. A levegő rezgései hullámok formájában tovaterjednek, elérik a fülünket és rezgésbe hozzák a dobhártyánkat. A dobhártya továbbítja a rezgéseket a belső hallószervekhez, míg végül az agyunk hangérzetté alakítja őket. De nemcsak a húros hangszerek, de az összes többi rezgéseket generál, és a levegőnek adja tovább. Egyes fúvós hangszerek esetében a síp lemezkéi rezegnek a közöttük átfújt levegőtől - ilyen például szaxofon vagy klarinét. Másoknál az üreges belsejükben levő levegőoszlop jön rezgésbe a belefújt levegő hatására, így működik a síp, pásztorfurulya, az oboa, a trombita vagy az orgona. Az ütőhangszerek esetében a rugalmas fém jön rezgésbe az ütés hatására (csengők, cintányér), vagy egy rugalmasan kifeszített bőrre mért ütés generál egyetlen hanghullámot, mint a dobok esetében.
A rádión közvetített zene is rezgések seítségével jut el hozzánk. A hangszerek és énekesek hangját a mikrofon alakítja át elektromos rezgésekké, az elektromos rezgéseket feldolgozzák, és elekromágneses hullámokra ültetik. Ezek fénysebességgel terjedve jutnak el a rádió antennájáig, ahol visszaalakulnak elektromos rezgésekké, végül a hangszóró membránját rezgésbe hozva hanghullámokká alakulva jutnak el a fülünkbe.

Vizsgáljuk meg az inga esetét. Egy fonalra felfüggesztett tárgyat egyensúlyi helyzetéből kimozdítva kétoldali lengéseket fog végezni az egyensúlyi helyzete körül. Lassulva kileng az egyik oldalra, az extrém helyzetben megáll egy pillanatra, aztán gyorsulva elindul visszafele. Az egyensúlyi helyzetében legnagyobb a sebessége, innét lassulva halad a másik extrém pontig, és a folyamat kezdődik elölről

Hasonlóképpen működik egy rugóra függesztett súly. Ha kimozdítjuk az egyensúlyi helyzetéből akkor igyekszik oda visszajutni, utána túlszalad rajta egészen az ellentétes helyzetig, és ez folyamatosan ismétlődik.

A kifeszített húr rezgése az előbbiekkel teljesen azonos. A megpendített húr kileng kétoldalra - a valóságban ezt nehéz szemmel követni, de a két extrém helyzete teljesen tisztán kivehető, a közbeeső állapotait csak elmosódva tudjuk érzékelni.

4. Newton I., II., III. axiómája, az erőhatások függetlenségének elve.

_{A tehetetlenség törvénye (Newton I. axiómája): Minden test megtartja egyenes vonalú egyenletes mozgását vagy nyugalmi állapotát, mindaddig  míg más testek ennek megváltoztatására nem kényszerítik => Tehetetlenség.}

_{Az erő (kölcsönhatás) törvénye (Newton II. axiómája): A mozgás megváltozása más testekkel való kölcsönhatás => mértéke az erő (F). A sebesség megváltozása arányos a testre ható erővel: az arányossági tényező reciproka a tömeg, az m. Azt fejezi ki, hogy a test mennyire áll ellent az erőnek, mennyire akarja mozgását megtartani. Minél nagyobb annál inkább, így az m a mozgás megtartó képességének, a tehetetlenségnek a mértéke, így ezt a tömeget a test tehetetlen tömegének nevezzük. Az előzőek szerint: komponenseként egy-egy másodrendű differenciálegyenletet (összesen három) jelent,  amik F(Fx,Fy,Fz) ismeretében, az említett kezdeti feltételek mellett (r(t=0)=r0(x0, y0, z0) és v(t=0)=v0(v0x, v0y, v0z)) megoldhatók.} 

_{Erő ellenerő törvénye (Newton III. axiómája): Minden erővel szemben fellép egy ugyanolyan nagyságú, de ellentétes irányú ellenerő.}

4. Newton IV. törvénye:  erőhatások függetlensége, a szuperpozició elve

Ha az anyagi pont egyidejűleg több hatásnak is ki van téve, azaz több erő hat, akkor együttes hatásuk egyetlen ú.n. eredő erővel helyettesíthető. Eredő erő az egyes erők vektori összege.

Az eredő

fogalma a fizikában elég széleskörűen alkalmazott fogalom. Az eredő akármi azt az egyetlen akármit jelenti, amely hatásában helyettesít az akármik szóbanforgó rendszerét. A mondat zavarossága azonnal oldódni látszik, ha az akármi-t az alkalomhoz illő konkrét fizikai fogalommal helyettesítjük pl. ellenállás, kapacitás, erő, .. stb.

Az ugyanezen néven futó egy másik állítás az erőhatások függetlenségének elve. Eszerint ha az és pontszerű testek valamint erőket fejtenek ki a pontra külön - külön ( a másik távollétében ), akkor egyidejű fellépésük esetén az eredeti és erők nem változnak (?).

Ezen törvény teszi lehetővé, hogy erők hogy összegzésével, erők rendszere helyett egyetlen erővel az un. eredő erővel végezzük számításainkat. Legalább ennyire fontos és hasznos ugyanezen törvény visszafelé olvasása is, amely az erők felbontását teszi lehetővé. Eszerint bármely erő helyettesíthető olyan erőkkel, amelyek vektori összege az eredeti erőt szolgáltatja. Klasszikus példa erre egy lejtőre helyezett testre ható nehézségi erő (súlyerő) felbontása a lejtőre merőleges Fm, és egy lejtővel párhuzamos Fp összetevőre. Itt a két erő hatásában helyettesíti a függőleges mg súlyerőt.

5. A mozgásegyenlet megoldása. Erőtörvények.

A bolygómozgás. Kepler törvényei.

M tömeg (Nap) áll az origóban, gravitációs terében m tömegű tömegpont (bolygó) mozog.  A mozgásegyenlet:  

A mozgásegyenlet megoldása bonyolult matematikai feladat. A mozgás lényeges sajátságait Kepler régóta ismert törvényei fogalmazzák meg:

I. törvény: A bolygó ellipszispályán kering a Nap körül, az ellipszis egyik fókuszában a Nap van.

II. törvény: A Naptól a bolygóhoz húzott vezérsugár egyenlő idők alatt egyenlő területeket súrol (a felületi sebesség állandó).

III. törvény: A Naprendszer bolygóira a bolygók keringési idejének négyzetei úgy aránylanak egymáshoz, mint pályáik nagytengelyeinek köbei.  

Az, hogy a pálya ellipszis, a differenciálegyenlet részletes megoldásából adódik. Itt ezt nem végezzük el, csak arra mutatunk rá, hogy az erőtér centrális, ezért a bolygó impulzusmomentuma állandó. Ebből közvetlenül következik Kepler II. törvénye, valamint az, hogy a pálya síkgörbe.

Kepler III. törvényét körpályák esetére szemléltetjük. Ha a bolygó körpályán mozog egyenletesen, akkor a következő összefüggés áll fenn a T keringési idő és az R pályasugár között:

      m a_cp = F,    azaz    m r (2ð/Ô) ãmM/r² 

Átrendezve:

      r³ / T² = ãM/ 4ð

Ebből látható, hogy r³/T² az egész Naprendszerre jellemző állandó mennyiség.

Kéttest-probléma      

Tegyük fel, hogy az M és m tömegpont között csak a gravitációs erő hat, de most engedjük meg az M mozgását is. Ez az ún. kéttest-probléma. A mozgásegyenletek:  
 

Látható, hogy , tehát a rendszer tömegközéppontjának gyorsulása zérus, sebessége állandó. (Hogy a tömegközéppont sebessége inerciarendszerben állandó, az közvetlenül jön az impulzusmegmaradás tételéből is.) Ezért bevezethetünk egy olyan inerciarendszert, amiben a tömegközéppont áll. Koordinátarendszerünk origója legyen az álló tömegközéppontban. Ekkor M helyvektora kifejezhető:

      R = - m/M r 

és m mozgásegyenlete: 

A kapott egyenlet pontosan ugyanolyan, mint a bolygómozgás egyenlete, csak a konstansok értéke más. Tehát Kepler I. és II. törvényei most is érvényesek: a bolygó és a Nap is ellipszispályán mozog, az ellipszis fókusza a tömegközéppontban van.  

Az úgynevezett háromtest-probléma, amikor három tömegpont mozog, és közöttük csak gravitációs erő hat, egyáltalán nem hasonlít az előző egy- és kéttest-problémához. Ilyenkor a megoldás nem fejezhető ki elemi függvényekkel, továbbá előfordul, hogy a megoldás kaotikus.

6. A Newton-féle gravitációs törvény. A Cavendish kísérlet. A bolygók mozgása (Kepler törvények).

égi mechanika

Az égitestek valóságos mozgásával foglalkozó csillagászati tudomány. Fő feladata a megfigyelt pozícióadatokból az égitestek pályájának, esetleg tömegének és alakjának a meghatározása. Alapja a Newton-féle gravitációs törvény.

Isaac Newton 1687-ben megjelent "Principia" című munkájában fejti ki az egyetemes tömegvonzás törvényét, amelynek lényege, hogy a világmindenségben az égitestek mindegyike vonzást gyakorol egymásra. Két test között a kölcsönös vonzóerő a testek középpontjait összekötő egyenes mentén hat. Két test között fellépő vonzóerő arányos a testek tömegével és fordítva arányos a távolságuk négyzetével, ahol az úgynevezett gravitációs állandó az arányossági tényező. Newton kimutatta, hogy ugyanaz az erő szabályozza a Hold Föld körüli, illetve a bolygók nap körüli keringését mint amelyik az almák lehullását.

Kepler-féle törvények. Bolygók mozgása. A Föld keringése a Nap körül.

I. törvény: A bolygók ellipszis pályákon keringenek, amelyeknek egyik gyújtópontjában a Nap áll (a numerikus excentricitás Föld esetében e

II. törvény: A Naptól a bolygókhoz húzott rádiuszvektor egyenlő időközök alatt egyenlő területeket (területi sebesség: dq/dt) súrol:

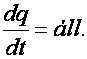(d5.1)

III. törvény: A bolygók keringési időinek (T) négyzetei úgy aránylanak egymáshoz, mint az ellipszispályák nagy tengelyeinek (r) köbei (más megfogalmazásban: a keringési idő négyzetét osztva az ellipszispályák nagy tengelyeinek köbével, minden bolygóra ugyanazt az értéket kapjuk):

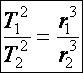másképpen (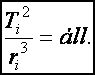d5.2)

ahol i=1, 2,..9 (Merkur, Vénusz,.....Plutó)

A Földről indított műholdak sebesség értékei:

Első kozmikus sebesség:
                   8 km/s ahol g=9,81m/s² R=6738 km (d5.3)

Második kozmikus sebesség

11 km/s 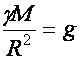(d5.4)
Geostacionárius pálya 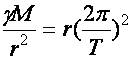r=42000 km (d .5)

A Newton-féle gravitációs erőtörvény származtatása.

A Napnak a bolygókra gyakorolt hatását leíró erőtörvény származtatásának lépései a Newtoni mechanika elvei alapján a következőkben kerül bemutatásra. (mivel ennek a gondolatsornak, az általánosítással együtt, valamint a Cavendish-féle kísérlettel együtt, alapvető szerepe van az egész fizikát és az eddigi világképünket érintően, ezért ennek részletesebb bemutatása következik itt. Ennek lépései a következők:

1. Tapasztalat: Kepler III. törvénye a Nap Vénusz, Föld, Mars, Jupiter bolygók mozgásáról (helykoordináta-idő függvényéről).

2. Ebből kell kifejeznünk a bolygó mozgása során tapasztalt gyorsulását. Közel körpályán haladnak, tehát a TP kinematikája szerint gyorsulása "centripetális". A centrumban a Nap "áll", Ő a centripetális hatás "kiváltója".

3. Ha beírjuk a dinamika alapegyenletébe a bolygó tömegét és gyorsulását, megkapjuk a Nap által rá gyakorolt hatás erőtörvényét. (Newton III. axiómája szerint a bolygók is ugyanakkora erővel hatnak a Napra) (1686)

4. Ezután következik Newton általánosítása, hogy ilyen hatás minden test között "létezik", csak a többi hatáshoz viszonyítva nagyon kicsi, ezért "nem tűnik fel". A testek közötti hatás kimérésére nagyon extra berendezést kellett készíteni. Ez az elméleti "jóslat" után csak 110 év múlva realizálódott. A Cavendish az általa készített torziós ingával 1791 mérte ki a g értékét.

Részletes ismertetés:

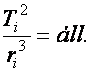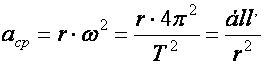
Þ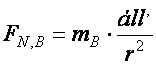

Þ  Þ 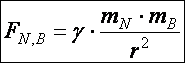 (d5.6)

Elméletileg, még "jósolni kell" arról, hogy egy kiterjedt test esetében a felszínétől "kifelé", milyen távolságfüggést "sejthetünk"? Erre a kiterjedt homogén, gömb alakú testre történő, térfogati integrálást felhasználó számolás adja azt az eredményt, hogy a felszíntől "kifelé" a gravitációs hatásának távolságfüggése olyan, mint a tömegközéppontjába 2képzelt", azonos tömegű, pontszerű test hatása.

Ha az általánosítást elfogadjuk, akkor a Föld is ugyanilyen erőtörvény szerint hat a rajta levő, és a körülötte keringő testekre. A felszínén (r=R) a 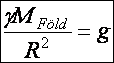(d5.7) értéke kimérhető, g értékét a Cavendish-féle ingával történt mérésekből elfogadva a Föld tömegére kaphatunk értéket. A Föld térfogatát ismerve, pedig az átlagsűrűségét tudjuk számolni.

7. A súlyos és tehetetlen tömeg. Eötvös kísérlete.

A folyadékok felületi feszültségének a nagyságát leíró egyik alapösszefüggés az Eötvös-törvény. A nehézségi gyorsulás változását Eötvös-egységekben mérjük. A Földön elmozduló testek súlyának megváltozását Eötvös-hatásnak nevezzük. A tehetetlen és a súlyos tömeg azonosságának az igazolása, ami az általános relativitás elméletének mindmáig a legdöntőbb bizonyítéka, az Eötvös-kísérlet. A nehézségi gyorsulásnak a föld mélyén rejtőző eltérő sűrűségű tömegek hatására bekövetkező változásait mérő egyik legnevezetesebb eszköz az Eötvös-féle
torziós inga, más néven horizontális variométer.

Vizsgáljuk meg, mi történik abban az esetben, ha a rugó elszakad, vagy levágjuk a rugóra függesztett

tömeget. Ekkor megszűnik az a rugóerő, mely egyensúlyt tartott a súlyerővel, de változatlanul

ugyanaz az erőtér fog ugyanarra a testre hatni. Így a test a rá ható eredő erő, a súlyerő hatására Newton

II. F ma törvényének megfelelően gyorsuló mozgást fog végezni. Ha a légellenállástól eltekintünk,

a test a szabadesés gyorsulásával, a g nehézségi gyorsulással fog mozogni, tehát

G mtg

ahol mt a test azon tulajdonságát jellemzi, hogy adott nehézségi erőtérben mennyire képes ellenállni

annak a gyorsító erőnek, amely a mozgásállapotát igyekszik megváltoztatni. A test e dinamikai tulajdonságát

az mt "tehetetlen" tömegének nagyságával jellemezhetjük.

Tekintettel arra, hogy a (8) és a (9) egyenletek baloldalán ugyanaz a súlyerő szerepel, ezért

msE mtg

Galilei olasz természettudós több mint 300 évvel ezelőtt egyidejűleg két testet: vas és fagolyót ejtett

le, és azt tapasztalta, hogy a két test a nagy súlykülönbség ellenére gyakorlatilag egyidőben ért a

talajra. Eötvös Loránd továbblépett, és az akkori technikai lehetőségeknek megfelelően a kilencedik

jegyig terjedő pontossággal igazolta a súlyos és a tehetetlen tömeg azonosságát (Renner, 1964; Perjés

. Einstein az ekvivalencia-, tehát a súlyos és a tehetetlen tömeg azonossága elvére építette fel az

általános relativitás elméletét. Minden elméleti fizikai megfontolás és minden megfigyelés amellett

szól, hogy a súlyos és a tehetetlen tömeg ugyan a testek két teljesen eltérő tulajdonságát jellemzi,

mégis a két mennyiség egyenlő egymással (Misner et al. 1973), tehát az

ms mt

egyenlőség miatt a (10) alapján

E g

Eszerint tehát a szabadon eső test gyorsulása, a nehézségi gyorsulás, irány, értelem és nagyság szerint

megegyezik a nehézségi térerősséggel. Fogalmilag, azonban a kettőt megkülönböztetjük, és

mindegyiket a maga helyén használjuk. Így, pl. a nehézségi erőtér potenciálját az (5) szerint a térerősséghez

rendeljük (így lesz a jellege fajlagos munka). Az eredmény tulajdonképpen nem is meglepő,

hiszen a (11) egyenlőség elfogadása után a (12) nem más, mint Newton II. törvényének a tömegegységre

vonatkoztatott alakja, ami a keletkező gyorsulást és az őt létrehozó erőt kapcsolja öszsze.

3. ábra. A gyorsuló erőtér hatása

Eddig a kérdést a newtoni gravitáció elmélet alapján tárgyaltuk. Nézzük meg a kérdést az általános

relativitás elmélet alapján. Végezzünk el egy fontos gondolatkísérletet Einstein ötlete alapján (Jones,

Childers, 1990)! Képzeljünk el egy űrhajót a világegyetem olyan távoli részén, ahol sem a közeli, sem a

távoli környezetben semmiféle tömegek nem találhatók és ennek megfelelően a gravitációs erőtér

8. Az impulzus fogalma. Az impulzus megmaradásának tétele. Pontrendszerekre vonatkozó impulzus vagy súlyponttétel.

Az impulzus (vagy néha lendület) általában véve a test azon törekvésének mértéke, hogy megtartsa mozgását annak irányával (azaz vektormennyiség) együtt. Megmaradó mennyiség, azaz zárt rendszer összes impulzusa állandó.

Az impulzus (lendület) egy fizikai vektormennyiség, ami egyenlő a test v sebességének és m tömegének a szorzatával:

I = mv

Nemcsak nagysága, hanem iránya is van tehát. Koordinátarendszerfüggő mennyiség, azaz ha egy objektumnak van valamekkora impulzusa, akkor az impulzusa a konkrét koordinátarendszerben akkora.

Impulzusmegmaradás

Mai tudásunk szerint az impulzus megmaradó mennyiség. Az impulzusmegmaradás szerint a világegyetem összes objektumának teljes impulzusösszege soha nem változik. Ennek egyik következménye, hogy akármilyen rendszer tömegközéppontja megtartja egyenes vonalú egyenletes mozgását mindaddig, amíg külső erő annak megváltoztatására nem kényszeríti.

Az impulzusmegmaradás szerint egy zárt rendszer (olyan rendszer, melyben csak belső erők hatnak) összimpulzusa az időben állandó. Ezt mondja ki Newton első törvénye, ami a harmadik Newton-törvény (hatás-ellenhatás) egyik következménye, s amit az impulzusmegmaradás törvénye diktál, mivel az erő az impulzusátadással arányos.

Mivel az impulzus vektromennyiség, iránya is van. Jól szemlélteti ezt az elsütött ágyú, ahol a golyó impulzusa az egyik irányban ugyanakkora, mint a visszalökődő ágyúé az ellenkező irányban, csak az ágyú nagyobb tömege miatt az ágyú sebessége jóval kisebb, mint az ágyúgolyóé, de a sebességek és tömegek szorzata ugyanaz.

A kvantummechanikában

A kvantummechanikában egy részecske impulzusát a hullám-részecske kettősség következtében a következőképpen lehet kifejezni:

ahol h a Planck-állandó, λ pedig a részecske De Broglie-hullámhossza.

Az impulzustétel

A test impulzusának változási sebessége (dp/dt) egyenlő a testre ható külső erők eredőjével (F):

dp/dt = F

Egyetlen tömegpont esetén F természetesen egyenlő a pontra ható erők eredőjével, hiszen ilyenkor minden erő külső erő. Az impulzustétel egyenértékű a II. axiómával, ha a tömeg időben konstans, ugyanis ekkor dp/dt = ma. Newton a II. axiómát nem a ma szokásos alakban, hanem az impulzustétel alakjában fogalmazta meg.

Ha a tömeg időben változik, akkor az impulzustétel és a II. axióma egyszerre nem lehet igaz. Változó tömegű test például a rakéta: a hajtógázok távozása miatt a rakéta tömege csökken. Ebben az esetben a klasszikus mechanikai leírásban az impulzustétel nem érvényes, a II. axióma pedig igen.

A relativisztikus mechanikában a tömegpont tömege függ a test sebességétől. Ha a pont tömege a hozzá képest nyugvó inerciarendszerben m₀ (nyugalmi tömeg), akkor abban a rendszerben, amihez képest a pont v sebességgel mozog

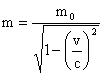
ahol c a vákuumbeli fénysebesség. A relativitáselméletben a fotonnak a nyugalmi tömege zérus, de a mozgási tömege nem.

Tekintsünk most egy pontrendszert és írjuk fel az impulzustételt a pontrendszer minden pontjára:

dp_i/dt = F_i^külső + S F_ki

Ha összegezünk i-re, akkor kapjuk az impulzustételt a kiterjedt testre:

dp/dt = F,                                                                                 i)

ahol F = S F_i^külső a külső erők eredője.

A belső erők összege a III. axióma miatt zérus (páronként kiejtik egymást: S S F_ki

(Megjegyzendő, hogy a (90) formula akkor is érvényes lenne, ha a jobboldalon F az összes (külső és belső) erő eredőjét jelentené. Ám ha impulzustételről beszélünk, akkor F alatt csak a külső erők eredőjét értjük, így mond többet a tétel.)

Ismertesse az anyagi pontrendszer impulzustételét!

I'=F
Az anyagi pontrendszer teljes impulzusának idő szerinti deriváltja egyenlő az anyagi pontrendszerre működő külső erők eredőjével.

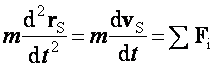
Ez a tömegközéppont mozgásának tétele vagy a súlyponttétel: egy mechanikai rendszer tömegközéppontja úgy mozog, mintha a rendszer egész tömege ebben a pontban lenne egyesítve, és a rendszer összes külső erőinek eredője erre a pontra hatna.

Ha

.

Ez az impulzus megmaradásának vagy súlypont megmaradásának tétele: ha a rendszerre nem hatnak külső erők ( zárt rendszer ), vagy ha ezek eredője zérus, akkor a rendszer impulzusa állandó, azaz a súlypont egye­nesvonalú egyenletes mozgást végez, vagy nyugalomban van.

A súlyponttétel jogosít fel arra, hogy a kiterjedt testet sokszor anyagi pontnak tekinthessük.

9. Az impulzusnyomaték (impulzusmomentum) fogalma. Az impulzusnyomaték tétele. Pontrendszerekre vonatkozó impulzusnyomaték tétel.

Az impulzusnyomaték tétele

Az impulzusnyomaték pontra vonatkozóan.

Az impulzusnyomaték, mint vektor.

Egy pontszerű test adott O pontra vonatkoztatott impulzusnyomatékán az

N = rIsinJ

illetve

N = [rI]

vektormennyiséget értjük.

Az impulzusnyomaték tétele:

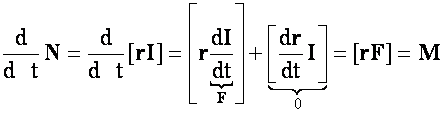
v I

egy pontszerű test adott pontra vonatkoztatott impulzusnyomatékának idő szerinti differenciálhányadosa egyenlő a testre ható erő ugyanezen pontra vonatkozó forgatónyomatékával.

Több tömegpontból álló rendszer esetén:

A mozgásegyenletek:

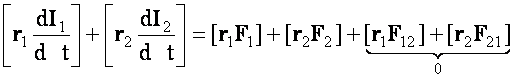
ugyanis

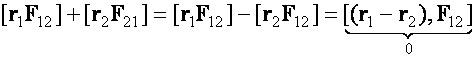
Eredményünket n tömegpontból álló rendszerre általánosítva:

Eredményünket n tömegpontból álló rendszerre általánosítva:

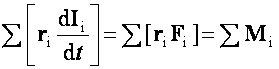
Most megmutatjuk, hogy

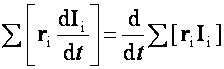
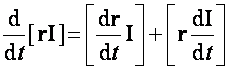
ezzel állításunkat igazoltuk.

Összefoglalva, az impulzusnyomaték tétele több tömegpontból álló rendszer esetén:

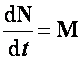vagy ,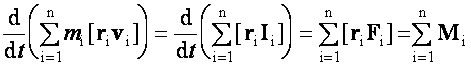

egy mechanikai rendszer impulzusnyomatékának idő szerinti differenciálhányadosa egyenlő a rendszerre ható külső erők forgatonyomatékának eredőjével.

Az M és N nyomatékok a választott O kezdőpontra vonatkoznak, amely az inerciarendszer bármely nyugvó pontja lehet.

Ha M = 0, akkor N = állandó:

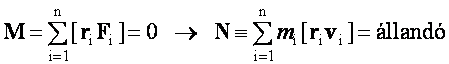
Ez az impulzusnyomaték megmaradásának tétele: ha a rendszerre nem hatnak külső erők ("zárt rendszer ), vagy ha a külső erők forgatónyomatékainak eredője nulla, akkor a rendszer impulzusnyomatéka állandó.

Egy tengely körül forgó merev test impulzusnyomatékának

a tengellyel párhuzamos komponense

r_i v_i

v_i a rajz síkjára merőleges

Mivel r_i v_i, N_i =

= m_i[r_iv_i] abszolút értéke:

N_i = m_ir_iv_i ,

így

N_iZ = m_ir_iv_icosJ_i

Ámde:

r_icosa_i = l_i és v_i = w_Zl_i

és így

Összegezve:

ahol a

mennyiséget a merev test (pontrendszer) Z tengelyre vonatkozó tehetetlenségi nyomatékának nevezzük.

10. A munka fogalma. Energia. A kinetikai energia tétele. A mechanikai energia megmaradásának tétele.

MUNKA, ENERGIA, TELJESÍTMÉNY

(1) Egyenesvonalú mozgást végző tömegpontra ható állandó F erő által a tömegponton végzett munka:

W = F s cos a , ahol.. s a megtett út,

a az F erő és a sebesség által bezárt szög.

Más alakban: W = F Dr, Dr az elmozdulás.

Általános esetben (görbevonalú mozgás és változó erő) a munkát közelítőleg úgy számíthatjuk ki, hogy a pályát kis szakaszokra bontjuk, amelyeken belül az erő állandónak, a mozgás egyenesvonalúnak tekinthető. A munkát ezen kis szakaszokon a fenti formulával. kiszámítjuk, majd összegezzük a különböző szakaszokra számolt munkákat. A pontos számítás integrál felhasználásával történhet. A munka egysége a joule: 1 J = 1 Nm

(2) A munka additív a pályára nézve: az összes munka egyenlő az egyes pályaszakaszokon végzett munka összegével. A munka additív az erőre igézve is: két erő eredőjének munkája egyenlő az egyes erők által végzett munkák összegével.

(3) A teljesítmény (P) az időegység alatt végzett munka. Ha P időben állandó, akkor P = W/t, ahol W a t idő alatt végzett munka. Általános esetben (azaz, ha P állandóságát nem tételezzük fel) W/t az átlagteljesítményt adja meg

A teljesítmény egysége a watt: 1 W = 1 J/s.

(4) Bizonyos esetekben a munka csak a kezdő- és végállapottól függ, de nem függ a folyamattól. Ilyenkor bevezethetjük az energiát, ami csak az állapot függvénye, és a munka az energia megváltozásával egyenlő.

Tömegpont kinetikus (mozgási) energiája

E_k = ½ mv² ,    ahol m a tömegpont tömege,

v a tömegpont sebessége.

A kinetikus energia additív, így n db tömegpontból álló pontrendszer kinetikus energiája az egyes tömegpontok kinetikus energiájának összege:

E_k = ½

(6) A munkatétel.

W = DE_k ,      DE_k = E_k2 - E_k1

Itt DE_k a test (tömegpont vagy kiterjedt test) kinetikus energiájának megváltozása, W pedig a testre ható erők összes munkája a folyamat közben. Kiterjedt testnél a belső erők munkáját is figyelembe kell venni.

(7) Konzervatív erőtér. Tegyük fel, hogy a tömegpontra ható erő csak a helytől. függ, az időtől és a sebességtől nem. Ha létezik olyan E_p(r) skalártér, hogy

W = - DE_p ,       DE_p = E_p2 - E_p1

akkor azt mondjuk, hogy az erőtér konzervatív, E_p pedig az erőtérben levő tömegpont potenciális (helyzeti) energiája.

A potenciális energia értékét önkényesen megadhatjuk egy tetszőleges pontban; előírhatjuk pl., hogy E_p = 0 legyen ott. Ennek az önkényes adatnak a megváltoztatása a potenciális energia értékét minden pontban ugyanúgy megváltoztatja, de két pont közötti különbségképzés eredményét nem befolyásolja.

(8) A tömegpont mechanikai energiája:

E_m = E_k + E_p.

Konzervatív erőtérben érvényes a mechanikai energia megmaradási tétele: E_m = állandó.

(9) Ha a konzervatív erőkön kívül a tömegpontra súrlódási erő is hat, akkor a mechanikai energia a mozgás során csökken.

Hatásfok. Hatásfokról akkor beszélhetünk, ha a munkát feloszthatjuk "hasznos" munkára (W_h) és veszteségre (W_v):

W = W_h + W_v

A hatásfok:     h W_h /W.

A kinetikus és potenciális energián kívül egyéb energiafajták is vannak. Általánosan érvényes az energia megmaradásának tétele:

Zárt rendszer összenergiája időben állandó.

Zárt rendszernek nevezünk egy olyan rendszert, amelyet külső hatás nem ér.

Mozgási vagy kinetikai energia

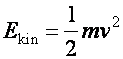
A kinetikai energia tétele

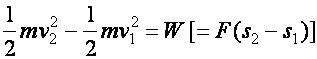
A mechanikai energia megmaradásának tétele

E_pot + E_kin º E = konstans,

ha a tömegpontra ható erők eredője konzervatív.

Mechanikai energia megmaradásának tétele :

        A testre ható erők eredőjének munkája egyenlő a test mozgási energiájának megváltozásával

11. Az ütközések tárgyalása a megmaradási törvények alapján. Rugalmas és rugalmatlan ütközés.

Az ütközések típusai:

Rugalmas ütközés: benne nem jön létre maradandó alakváltozás. Erre érvényes a lendület megmaradás törvénye mellett a mechanikai energia megmaradási törvénye (lásd később) is.

Rugalmatlan ütközés: benne maradandó alakváltozás jön létre, csak a lendület- és az általános energia megmaradási törvény alkalmazható rá.

Tökéletesen rugalmatlan ütközés ugyanolyan, mint a rugalmatlan, csak a testek az ütközés után együtt mozognak tovább.

Egyéb csoportosítások: centrális és nem centrális; egyenes és ferde ütközések

A rugalmas ütközések

A rugalmas ütközések vizsgálatához feltételezzük, hogy az ütköző testek anyaga tökéletesen rugalmas, az ütközéskor nem lép fel súrlódás. A testek forgó mozgást nem, csak haladó mozgást végeznek, a súlypontjaikat összekötő egyenes mentén, centrálisan ütköznek egymással. Legyen testek tömege m1 és m2, ütközés előtti sebességük v1e, v2e, ütközés utáni pedig v1u, v2u. A testek tömegének és kezdeti sebességeiknek függvényében szeretnénk az ütközés utáni sebességeket meghatározni. A számításokhoz a mozgási energia és az impulzusmegmaradás törvényét fogjuk felhasználni:

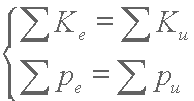
12. Merev test. A merev test mozgásának leírása. A merev testre ható erők összetevése.

Merev test: amelynek pontjai a fellépő erők hatására egymáshoz képest csak elhanyagolható mértékben mozdulnak el Û nincs alakváltozás.

Helyzetét három nem egy egyenesbe eső pontjának helyzete egyértelműen meghatározza.

Ez 3 3 = 9 adat az x, y, z koordináta rendszerben, de mivel

.......... ..... ...... .......... ..... ...... ..... ,

.......... ..... ...... .......... ..... ...... ..... ,

a 9 adat közül csak 6 független egymástól Û a merev test helyzetét, ha a test szabadon mozoghat, 6 független adat határozza meg Û a szabad merev testnek 6 "szabadsági foka" van.

Merev test síkmozgása: ha pontjai egy adott síkkal párhuzamosan mozognak,összetehető

egy haladó és egy forgó mozgásból.

A merev testre ható erők összetevése

Az erővektor eltolhatósága

Az erők összetevése, ha a támadásvonalak egy síkban vannak

és nem párhuzamosak

Párhuzamos erők összetevése

Két párhuzamos és megegyező irányú erő összetevése

Két párhuzamos és megegyező irányú erő összetevése

F = F₁ + F₂    és F₁k₁ = F₂k₂ .

Két párhuzamos és ellentétes irányú (de nem egyenlő nagyságú)

erő összetevése

F = F₁ F₂   és F₁k₁ = F₂k₂ .

Két antiparalel és egyenlő nagyságú erő (erőpár) összetevése

Nem helyettesíthető egyetlen erővel sem.

13. Forgatónyomaték pontra vonatkozóan. A forgatónyomaték, mint vektor. Erőpár forgatónyomatéka. A merev test egyensúlyának általános feltételei.

Forgatónyomaték

Forgatónyomaték tengelyre vonatkozóan

A Z tengelyre merőleges síkban ható F erő Z tengelyre vonatkozó forgatónyomatéka:

M_Z F k

Forgatónyomaték pontra vonatkozóan.

A forgatónyomaték, mint vektor

k = rsinJ miatt M = Fk = rFsinJ

M = [rF] .

(Az M iránya merőleges az r és F meghatározta síkra a jobbcsavar szabály szerinti értelemben.)

Az erőpár forgatónyomatéka

Adott F(P₁) és F(P₂) erőkből álló erőpárok O pontra vonatkozó forgatónyomatékán az

M = [r₁F] + [r₂, F] = [r₁F₁] [r₂F] = [(r₁ r₂),F] = [lF]

vektori mennyiséget értjük, amely független az O vonatkoztatási pont helyzetétől.

A merev test egyensúlyának általános feltételei

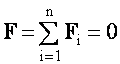
és

,

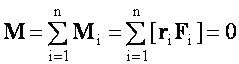ahol a forgatónyomaték felírásakor a választandó/választható pont a testen kívüli, de hozzá képest nyugvó pont is lehet.

14. Merev test forgása rögzített tengely körül. A tehetetlenségi nyomaték. A forgó és haladó mozgás megfelelő mennyiségei közötti analógia.

MEREV TEST FORGÁSA RÖGZÍTETT TENGELY KÖRÜL

(1) A rögzített tengely körül forgó merev test minden pontja körpályán mozog: a kör sugara a pontnak a tengelytől mért távolsága. A rögzített tengely körül forgó merev test szabadsági foka 1, a test helyzetének leírása célszerűen egyetlen szöggel történhet: kiválasztjuk a test egy P pontját, merőlegest húzunk belőle a tengelyre, és a helyzetet azzal az a szöggel adjuk meg, amit e merőleges bezár egy vonatkoztatási iránnyal:

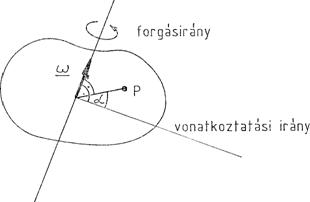
2.15.1 ábra

A szög bevezetése sok önkényes elemet tartalmazott, de a forgás közben bekövetkező Da szögváltozás az egész merev testre ugyanaz, és független az önlényes választásoktól!

(2) A szög változási sebessége a szögsebesség: .

A szögsebesség az egész merev testre ugyanannyi. Szokásos ennek a szögsebességnek irányt is tulajdonítani: az irány a forgástengely iránya. A kétféle irányítottság között a jobbrendszer (1.4.6) követelménye alapján választhatunk.

A merev test minden pontja ugyanolyan szögsebességű körmozgást végez. A tengelytől r távolságra levő P pont sebességének nagysága: v = r w. A forgástengelyen levő pontok tehát nyugalomban vannak.

(3) A szögsebesség változási sebességét szöggyorsulásnak nevezzük: . A forgómozgást egyenletesnek nevezzük, ha a szögsebesség konstans; egyenletesen változónak, ha a szöggyorsulás konstans.

Egyenletes forgómozgásnál

a a w t,              a : kezdeti szög

Egyenletesen változó forgómozgásnál:

w w b t,               w : kezdeti szögsebesség

a a w t + ½ bt²

(4) A forgómozgás alapegyenlete

Q b = M,        Q: a forgástengelyre vonatkoztatott tehetetlenségi nyomaték

b: szöggyorsulás

M: a forgástengelyre vonatkoztatott külső forgatónyomaték

(5) Analógia a haladó és a forgómozgás között

Az x tengely mentén mozgó tömegpont helyét az x koordinátával adhatjuk meg, tehát szabadsági foka éppúgy, mint a rögzített tengely körül forgó merev testnek. Képezhetünk egy "szótárat", ami kölcsönösen megfelelteti a tömegpont egyenes vonalú egyenletes mozgásánál és a merev test rögzített tengely körüli forgómozgásánál fellépő mennyiségeket egymásnak. A formulák szerkezete ugyanolyan, csak a megfelelő mennyiségeket kell behelyettesíteni ahhoz, hogy egy, az egyenesvonalú mozgásra megismert formulából forgómozgásra érvényes formulához jussunk.

"Szótár":

A szótár használatát a forgási kinetikus energia példáján mutatjuk be. Minthogy a tömegpont kinetikus energiája E_k = ½ mv², a megfelelő mennyiségek behelyettesítésével kapjuk a forgási kinetikus energiát:

E_k = ½ Qw

(6) Állandó tengely körül forgó merev test külső hatásoktól mentesen (magára hagyva) egyenletes forgómozgást végez. Jó közelítéssel ilyen a Föld tengely körüli forgása. A valóságban mindig vannak veszteségek, amik végülis lefékezik a forgást.

15. A matematikai és a fizikai inga.

Matematikai inga

A matematikai inga egyik végén felfüggesztett, ℓ hosszúságú, nyújthatatlan és tömegtelen kötélre erősített m tömegű tömegpont. Nemzérus kötélerő esetén a tömegpont a felfüggesztési pont körüli ℓ sugarú gömbfelületen mozoghat, ezért gömbi ingának is nevezzük. Két speciális esetet veszünk.

Síkinga

Tegyük fel, hogy a tömegpont a földi nehézségi erőtérben mozog, és a kezdősebesség olyan, hogy a pálya egy állandó függőleges síkban van, ez az inga lengési síkja. A pálya ilyenkor körív. Ábra! A mozgásegyenlet:

m = G + K (a)

Bontsuk fel a vektorokat tangenciális és centripetális (más szóval normális, esetünkben kötélirányú) összetevőkre. Vegyük figyelembe, hogy az s út és az a szög között az összefüggés: s = ℓa, a gyorsulás tangenciális komponense pedig a_t = ℓ. A mozgásegyenlet tangenciális komponense:

mℓ mg sina                                                                          (b)

m-mel egyszerűsíthetünk:

+ (g/l) sina = 0 (c)

Azaz a mozgás független az m tömegtől: ez minden esetben így van, ha a test pusztán a nehézségi és kényszererők hatása alatt mozog.

Kis szögű kitérésekre a<<1, alkalmazzuk a sina a közelítést, ekkor a mozgásegyenlet:

+ w a = 0 , w = g/l                                                              (d)

Ez pedig a harmonikus rezgőmozgás differenciálegyenlete. Az általános megoldás:

a a cos(wt+j (e)

ahol w a körfrekvencia, ahonnan a lengésidő: T = 2p.

Az a és j integrációs állandókat a kezdeti feltételek határozzák meg.

a a maximális szögkitérés, amplitúdó,

j pedig a kezdőfázis.

A síkinga síkját inerciarendszerben megtartja. A Föld tengely körüli forgását bizonyító első kísérletetek egyike volt a Foucault inga. Igen hosszú fonálon felfüggesztett inga esetén elérhető, hogy az inga sokáig lengjen, a súrlódás kicsi. Ilyen ingánál tapasztalható, hogy az inga lengéssíkja hosszú idő alatt változik, minthogy a Földhöz rögzített rendszer nem inerciarendszer.

Kúpinga

Ha a matematikai ingát megfelelő kezdősebességgel indítjuk el, elérhetjük, hogy az inga fonala a kúpszögű kúpfelületet írjon le, az m tömeg egy vízszintes síkban egyenletes körmozgást végezzen v sebességgel. ÁBRA! A mozgásegyenlet:

m = G + K , (f)

ahol K a kötélerő.

Mivel a mozgás egyenletes körmozgás, a gyorsulás a kör középpontja felé mutat és nagysága v²/ℓsina.

Az ábrából ezért a

tga = v² / gℓsina                                                                           (g)

összefüggés adódik.

Fizikai inga

Fizikai inga egy vízszintes rögzített tengely körül forgó merev test. A test tömegközéppontjának a forgástengelytől mért távolságát jelöljük s-sel, a test tömegét m-mel, a forgástengelyre vonatkoztatott tehetetlenségi nyomatékát Q-val.

A forgómozgás alapegyenletéből erre az esetre

Q d²a/dt² = mg s sina                                                                     ii)

ÁBRA!!!

Ez ugyanaz az egyenlet, mint az ℓ = Q/ms hosszúságú síkinga egyenlete. Tehát minden fizikai inga úgy mozog, mint az ilyen hosszúságú matematikai síkinga. Kis szögkitérésnél, amikor sina helyettesíthető a-val, kapjuk a harmonikus rezgés differenciálegyenletét, itt a forgás a szögkitérése időben szinuszosan változik, a lengésidő

T = 2p

16. Szabad tengelyek. Erőmentes pörgettyű. Pörgettyű forgatónyomaték hatása alatt.

Szabad tengelyek

åF_külső

Szabad tengelyek: állandó helyzetű, nem rögzített tengelyek

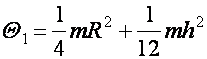
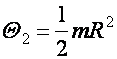
A b) és d) a legstabilisabb.

a > b > c

Q_A > Q_B > Q_C

és Q_C a legstabilisabb

Összefoglalva

åF = 0 és åM = 0 esetben a merev testnek általános esetben három, egymásra merőleges szabad tengelye van, nevezetesen a test súlypontján átmenő három fő tehetetlenségi tengely.

A szabad tengelyek stabilitására nézve fennáll: stabilis a forgás a legnagyobb és a legkisebb, labilis a forgás a középső tehetetlenségi nyomatéknak megfelelő tengely körül.

Legstabilisabb a legnagyobb tehetetlenségi nyomatékhoz tartozó tengely körüli forgás.

Erőmentes pörgettyű; nutáció

A súlypontjában alátámasztott, csavarral rögzíthető tengelyű  pörgettyű  kerekét forgassuk meg szimmetriatengelye körül, és hagyjuk magára! Azt tapasztaljuk, hogy a pörgettyű  - külső forgatónyomaték híján - a térben állandó helyzetű  tengely körül tartósan forog. (A szimmetriatengely, a pillanatnyi forgástengely és az impulzusnyomaték- vektor egyenese egybeesik.)
    Oldalirányú ütéssel billentsük meg a pörgettyű  tengelyét: azt látjuk, hogy a tengely - a térben állandó irányú egyenes körül - kúpfelületen mozog (IV.24. ábra).

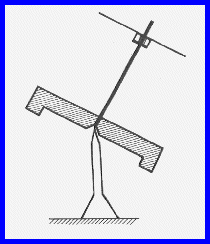
IV.24. ábra

    Ha a pörgettyű  tengelyének felső végére négyzethálós papírkorongot helyezünk, és a négyzeteket például sakktáblaszerűen fekete-fehérre képezzük ki, akkor azt is megfigyelhetjük, hogy a pillanatnyi forgástengely szintén kúpfelületet ír le a fentebb említett irány körül. (A pillanatnyi forgástengelyre eső négyzet éppen állni látszik, miközben a többi négyzet ekörül körpályán mozog. A pillanatonként mindig más-más helyen látható "álló" négyzetek összessége kört "rajzol" a korongon.) E két tengelynek a kúpfelületeket leíró mozgását nevezzük nutációnak. A térben állandó egyenes pedig az impulzusmomentum-vektornak az alátámasztási ponton átmenő hatásvonala.

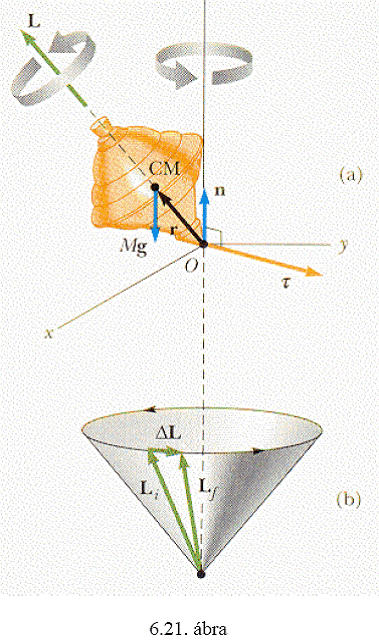
A pörgettyű mozgása

Nagyon érdekes mozgást figyelhetünk meg, ha gravitációs erőtérben egy szimmetrikus

merev test (un. szimmetrikus pörgettyű) szimmetriatengelye körül forog (6.21. ábra). Ilyen pl.

a búgócsiga mozgása. Ha a test a tengelye körül nagyon gyorsan forog, azt tapasztaljuk, hogy

bizonyos esetekben a forgástengelye a függőleges irány körül egy kúppalást mentén forgó

mozgást végez.

Pörgettyűnek egy tetszőleges alakú és tömegeloszlású merev testet nevezünk akkor, ha

a test egy rögzített, vagy rögzítettnek tekinthető pontja körül (O) körül foroghat. Ha a testet

egyik fő tehetetlenségi tengelye körül forgatjuk meg, a szögsebesség és a perdület vektor

egyirányú. Tetszőleges alakú és tömegeloszlású test esetén nehéz a fő tehetetlenségi

tengelyeket megtalálni és a testet (pörgettyűt) valamelyik fő tehetetlenségi tengely körül

megforgatni. Szimmetrikus test estén azonban ez nagyon egyszerű dolog, mivel a

szimmetriatengely egyúttal az egyik fő tehetetlenségi tengely. A gyakorlatban csak a

szimmetrikus pörgettyűvel foglalkozunk. A szimmetrikus pörgettyű három fő tehetetlenségi

nyomatéka közül kettő megegyezik, a test tömegközéppontja a szimmetriatengelyen van.

Szimmetrikus pörgettyű pl. egy homogén henger vagy más forgástest, ha a rögzített O pont a

test szimmetriatengelyének egy pontja. Két esetet különböztetünk meg: ha az O pont

megegyezik a test tömegközéppontjával, akkor a pörgettyű un. erőmentes pörgettyű; ha az O

pont nem egyezik meg a test tömegközéppontjával és gravitációs tér is jelen van, akkor

beszélünk az un. súlyos pörgettyűről. A következőkben a súlyos szimmetrikus pörgettyű

mozgását vizsgáljuk meg.

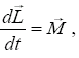
17. Egyenes vonalú egyenletes transzlációt végző viszonyítási rendszerek. A Galilei elv.

Egyenes vonalú egyenletes transzlációt végző koordináta-rendszerek

A klasszikus mechanika relativitási elve (a Galilei-féle relativitási elv):

az egymáshoz képest egyenes vonalú egyenletes transzlációt végző koordináta-rendszerek a mechanikai jelenségek leírása szempontjából teljesen egyenértékűek.

Ha az egyik ilyen rendszer inercia­rendszer, akkor a másik is az.

Inerciarendszer: olyan vonatkoztatási rendszer, melyben Newton I. törvénye érvényes.

Az inerciarendszer nem gyorsulhat. (Példa: egy induló-gyorsuló trolibuszban a nem kapaszkodó személy hátraesik, a trolibuszhoz képest gyorsul. Ennek okát nem találjuk semmilyen külső hatásban. A külső szemlélő szerint nem is gyorsul...)

Galilei-féle relativitási elv: az egymáshoz képest álló, vagy egyenes vonalú egyenletes mozgást végző vonatkoztatási rendszerek dinamikailag egyenértékűek. (Két ilyen rendszerből vizsgálva egy test mozgását a sebessége különböző lehet, de a sebesség megváltozása és így a gyorsulás is megegyező - nyilván a mozgásállapotot változtató hatások is megegyeznek. Példa: gyalogos mozgását vizsgáljuk a járdához ill. az egyenletesen mozgó villamoshoz képest...)

A Galilei-féle relativitási elv következménye, hogy ha találunk egyetlen inerciarendszert, akkor az ehhez képest nem gyorsuló összes vonatkoztatási rendszerek is mind inerciarendszerek lesznek.

18. Gyorsuló transzlációt végző viszonyítási rendszerek. A tehetetlenségi erő fogalma.

Inerciarendszerekhez képest gyorsuló vonatkoztatási rendszerekben a megfigyelő által észlelt jelenségek úgy játszódnak le, mintha az inerciarendszerben levő megfigyelő által észlelt erőkön kívül más erők is fellépnének. Ezeket nevezzük tehetetlenségi erőknek. Legegyszerűbb hétköznapi példa az, mikor ülünk a kocsiban, és egy erős fékezéskor előredőlünk. A kocsin kívüli megfigyelő ezt egyszerűen a bent ülő ember tehetetlenségének tulajdonítja. Viszont az autóban ülő megfigyelő nem tudja mással, csak tehetetlenségi erőkkel megmagyarázni a jelenséget.
Szokták ezeket az erőket virtuális erőknek is hívni, ugyanis az erő a definíciója szerint két test között lép fel. Itt erről nincs szó. A tehetetlenségi erőket tehát a gyorsuló vonatkoztatási rendszerben levő jelenségek megmagyarázására találták ki.

Inerciarendszerhez képest gyorsuló vonatkoztatási rendszerek

Mindenki tapasztalta már, hogy amikor egy egyenes vonalú pályán haladó jármű fékez

(gyorsulása negatív, ellentétes a sebességgel) az utasok előre esnek, mintha egy a gyorsulással

ellentétes irányú erő hatna rájuk. Hasonlóan, amikor az autó gyorsul, úgy érezzük, hogy a

gyorsulással ellentétes irányú erő az üléshez szorít bennünket. Amikor a jármű kanyarodik, a

benne ülő úgy érzi, hogy egy kifelé mutató erő szorítja hozzá az ajtóhoz. Ezek az erőket a

gyorsuló rendszerrel együttmozgó személy valóságosnak érzi, de ezek és a gyorsuló

vonatkoztatási rendszerben fellépő egyéb erők nem valódi erők, mert nem a testek

kölcsönhatása következtében lépnek fel. Ezek az erők kizárólag a gyorsuló rendszerben lévő

megfigyelő számára léteznek, a jelenséget inerciarendszerből leíró megfigyelő számára

nincsenek. Ezért a vonatkoztatási rendszer gyorsulása következtében fellépő erőket fiktív

vagy pszeudo erőknek is mondják. Mivel ezek az erők egyenesen arányosak a test

tehetetlenségével (tömegével), tehetetlenségi erőknek nevezzük őket. Gyorsuló

rendszerekben Newton II. törvénye csak akkor érvényes, ha a valódi erőkhöz hozzáadjuk a

tehetetlenségi erőket is.

19. Forgó viszonyítási rendszerekben fellépő tehetetlenségi erők. A centrifugális és Coriolis erő hatásai.

4.2.2. Inerciarendszerhez képest állandó szögsebességgel forgó vonatkoztatási rendszer

Vizsgáljuk meg, milyen tehetetlenségi erők lépnek fel állandó szögsebességgel forgó

vonatkoztatási rendszerekben. Ilyen pl. egy egyenletesen forgó korong. Forgó vonatkoztatási

rendszer esetén az anyagi pont helyzetének megadásához gömbi koordinátákat célszerű

használni. A K inerciarendszer és a K' forgó vonatkoztatási rendszer 0 és 0' origója legyen

egy pontban ( R rr ), a forgóasztal középpontjában. Így az m tömegű anyagi pont rr és rr

helyzetvektora a két vonatkoztatási rendszerben megegyezik (a z és z' tengelyek is

egybeesnek). Ahogy már a kinematika fejezetben is láttuk, az r szögsebesség vektor a

forgástengelyben van.

4.2.2.1. Állandó szögsebességgel forgó rendszerben nyugalomban lévő anyagi pont

Tekintsünk egy forgó korongon lévő tartóra fonállal felfüggesztett, kicsiny, m tömegű

testet (4.3. ábra). A test a forgó rendszerben nyugalomban van, a fonál a függőlegessel

szöget zár be.

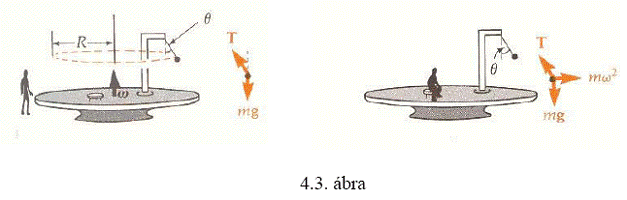
A K inerciarendszerbeli (a földön álló) megfigyelő szerint az m tömegű anyagi pont az

inerciarendszerhez képest R sugarú körpályán mozog r szögsebességgel. A testre két erő hat:

a nehézségi erő és a kötélben ébredő kényszererő. Ezen két erő eredője (a fonálerő T sin

vízszintes összetevője) adja a vízszintes síkban a kör középpontja felé mutató centripetális

erőt, mely a m tömegű test R centripetális gyorsulását okozza:

A K' forgó rendszerben lévő megfigyelőhöz képest az m tömegű anyagi pont

nyugalomban (egyensúlyban) van. A megfigyelő szerint a tengelytől R távolságban lévő, a

függőleges iránnyal szöget bezáró testre a nehézségi erőn és a fonálban ébredő

kényszererőn kívül egy harmadik, kifelé mutató tehetetlenségi erő is hat; ez a tehetetlenségi

erő kompenzálja a fonálerő T sin vízszintes összetevőjét. Ezt a forgástengelyre

merőlegesen kifelé mutató tehetetlenségi erőt centrifugális erőnek nevezzük, nagysága:

3. ábra készítette: Schlanger Š

4. Mindenki megtapasztalhatta a centrifugális erőt körhintázás közben, vagy autózás közben, amikor az autó kanyarodik, vagy akár biciklizéskor éles kanyarban.

20. Nyugvó folyadékok mechanikája (folyadékok jellemzése; hidrosztatikai nyomás; Arkhimédész törvénye).

Folyadékok jellemzése:

Alakjuk könnyen változtatható,

Térfogatuk nehezen változtatható, nagyon kis mértében, inkább nem.

Belső súrlódás (egymáson csúszó rétegek) v ≠ 0 esetén van, v = 0 esetén nincs Û nyugvó folyadékokban érintőleges vagy nyíróerők és feszültségek nincsenek.

Adhéziós erők.

Ideális folyadék: súrlódásmentes

Nyugvó folyadék szabad felszíne merőleges a külső erők eredőjére. (Nagy kiterjedésű vízfelületek a Föld alakját követik.) 

Tudjuk, hogy a szilárd halmazállapotú testeknek meghatározott alakja van, amely csak munkavégzés árán változtatható meg. A folyékony halmazállapotú anyagok felveszik az edény alakját, de részleges kitöltés esetén szabad felszínnel rendelkeznek, a légnemű vagy gáz halmazállapotú anyagok pedig a rendelkezésükre álló teret teljes egészében kitöltik.

Elsőként definiáljuk azt a két legfontosabb anyagjellemzőt, amelyre a folyadékokkal kapcsolatos jelenségek leírásához feltétlenül szükségünk lesz.

Az első ilyen jellemző az anyag sűrűsége, amelyet természetesen bármely más halmazállapotú testre is értelmezhetünk, a

hányadossal, ahol a figyelembe vett térfogatelem elegendően kicsi. Homogén tömegeloszlású test esetén természetesen a sűrűség az általánosan használt

összefüggéssel számítható.

A folyadékok másik fontos jellemzője a viszkozitás, amely szemléletesen a folyadék alakváltozással szembeni ellenállásának számértékét adja. Meg szoktuk különböztetni az dinamikai és a kinematikai viszkozitást, és a két mennyiség közötti kapcsolat az összefüggéssel adható meg.

Ahhoz, hogy a folyadékok mechanikájával kapcsolatos törvényeket a rendelkezésünkre álló matematikai eszközökkel meg tudjuk határozni, a vizsgált folyadékokkal kapcsolatban bizonyos feltételezésekkel kell élnünk. A továbbiakban tehát először olyan, ideálisnak tekintett folyadékokkal foglalkozunk, amelyek a következő tulajdonságokkal rendelkeznek:

• a folyadék a testet folyamatosan kitöltő, homogén kontinuum,
• összenyomhatatlan,
• belső súrlódása nincs, vagyis viszkozitása nulla,
• a folyadék belsejében húzófeszültség és kohéziós erő nem ébred.

Az ezekkel az elvi tulajdonságokkal rendelkező folyadékok esetén meghatározott összefüggések természetesen a későbbiekben általánosíthatók, vagyis érvényességük kiterjeszthető a valóságos folyadékok hidrosztatikai és áramlástani vizsgálataira is.

A nyugvó ideális folyadék egyensúlya: hidrosztatika

A nyugvó folyadék szabad felülete

Az ideális folyadék egyik alapvető tulajdonságaként említettük, hogy belső súrlódása nincs, vagyis a nyugvó folyadék határfelületén és belsejében az alakváltoztató hatással szemben nyírófeszültségek nem ébredhetnek. A nyugvó folyadék szabad felszínének egyensúlya tehát csak úgy állhat fenn, ha a szabad felszín mindenkor merőleges a helybeli nehézségi gyorsulás irányára, köznapi szóhasználattal élve vízszintes.

A folyadék nyomása

A folyadékokra egyaránt hathatnak térfogati és felületi erők. A térfogati erők között legfontosabb példaként említhetjük a nehézségi erőtér által kifejtett erőt, míg a felületi erők közül a folyadék nyomásából származó erőt tekinthetjük mértékadónak.

A nyomás a felületre merőlegesen ható erőnek és a felület nagyságának hányadosa:

Ha az erő, és ezáltal a nyomás a felület különböző pontjaiban nem egyenlő, a fenti hányados természetesen csak átlagos nyomásértéket definiál, ebben az esetben a lokális vagy helyi nyomás értékét a

hányados adja meg, ahol a választott felületelem már elegendően kicsi ahhoz, hogy a rá ható erő állandónak legyen tekinthető. A nyomóerő mindig merőleges a felületre, a felület irányításától függetlenül, ezért a nyomás skaláris mennyiség. A nyomás tehát irányfüggetlen, vagyis izotróp mennyiség, másrészt pedig homogén, azaz megegyezik a folyadék belsejében és határfelületén.

Ha feltételezzük, hogy a folyadékra térfogati erők nem hatnak, vagyis a nehézségi erőtér hatásától eltekintünk, akkor ebben az esetben a vizsgált folyadékra csak felületi erők hatnak, és megfogalmazhatjuk Pascal törvényét, amely szerint:

A folyadékra vagy gázra ható külső felületi erő által létrehozott nyomás a folyadékban vagy gázban minden irányban gyengítetlenül terjed.

Ez a törvény természetesen csak azokban a gyakorlati esetekben alkalmazható, amelyekben a nehézségi erőtér hatása a folyadékra ható külső felületi erőkhöz képest elhanyagolható, pl. hidraulikus emelők vagy prések, illetve hidraulikus vagy egyes légnyomással működő fékek esetében.

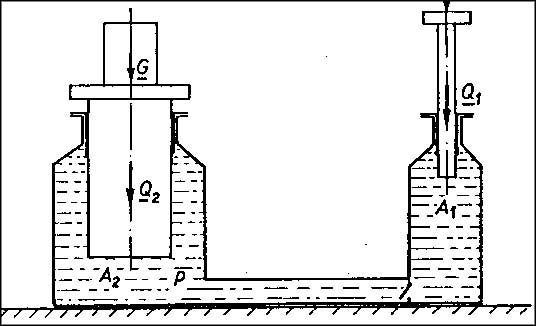
Egyszerű példaként említhetjük az ábrán vázolt hidraulikus emelőt, ahol a folyadék nyomásából származó erő mindkét oldalon egyensúlyt tart a dugattyú súlyerejével és a dugattyúra ható külső erővel:

.

Az egyenletből következő

kifejezés egyértelműen mutatja, hogy a felületek arányát megfelelően kicsire választva elérhető, hogy igen nagy terheket is emelni tudunk viszonylag kis erőkifejtéssel. A folyadék összenyomhatatlanságából következően a munkafolyadék térfogata állandó lévén a dugattyúk elmozdulása természetesen nem egyenlő, vagyis mechanikai munkát nem nyerhetünk, hiszen a kis erőt a dugattyú hosszú elmozdulása során kell kifejtenünk

Hidrosztatikai nyomás

Pascal-törvénye: súlytalannak képzelt nyugvó folyadék belsejében és határfelületén a nyomás mindenütt ugyanakkora, és független a tekintetbe vett felületelem irányításától. 

az összenyomhatatlanságból    q₁δs₁ = q₂δs₂ 

a virtuális munka elvéből    F₁δs₁ = F₂δs₂ 

így ,   azaz   p₁ = p₂ = p (állandó)

A hidrosztatikai nyomás

A következőkben vegyük figyelembe, hogy a folyadékra mindenkor hat a nehézségi erő, tehát vizsgáljuk meg a súlyos folyadék egyensúlyának feltételeit.

Ha a folyadék felszínén nem hat külső felületi erő, akkor a folyadék felszínétől mért h mélységben a nyomás értéke:

.

Amennyiben a szabad felszínre ható, általában -lal jelölt külső légköri nyomást is figyelembe vesszük, akkor az előbbi nyomás értéke:

.

Ezt az összefüggést a hidrosztatika alapegyenletének nevezik. A benne szereplő nyomások közül tehát -t külső légköri nyomásnak, a mennyiséget túlnyomásnak, és a kettő összegeként értelmezett nyomást abszolút nyomásnak nevezzük, ezekkel az elnevezésekkel tehát az előbbi egyenlet a

alakban írható fel.

Érdekes megállapítást tehetünk, ha vizsgáljuk a folyadék súlyából származó, a folyadékot tartalmazó edény aljára ható erők nagyságát különböző kialakítású edények esetén.

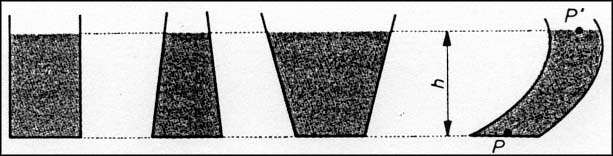
A folyadék mindegyik edényben azonos magasságú, tehát valamennyi tartály alján a túlnyomás .

A tartályok alaplapjainak felülete szintén egyenlő, így az ezen túlnyomásból származó, a tartály alaplapjára ható erő nagysága valamennyi esetben

.

Miután a folyadék súlyerejét a összefüggéssel határozhatjuk meg, és az edény alakjától függően a folyadéktérfogatok értéke más és más, látjuk, hogy a tartály aljára ható erő nem feltétlenül egyenlő a benne lévő folyadék súlyerejével, hanem annál nagyobb is vagy kisebb is lehet. Ezt a jelenséget hidrosztatikai paradoxonnak nevezzük.

A hidrosztatikai paradoxonban rejlő látszólagos ellentmondás természetesen feloldható, hiszen, ha az edény oldalfaláról a folyadékra átadódó erőket is figyelembe vesszük, folyadékra ható erők eredője zérusra adódik. Az edény oldalfalára ható, a folyadéknyomásból származó erők meghatározása azonban még egyszerű formájú edény esetében is összetett feladat, mert a nyomás a felületen nem állandó, hanem a mélységgel lineárisan változik. Az általa kifejtett erő tehát egy olyan, a felületen megoszló erőrendszer, amelynek intenzitása a mélységgel egyenesen arányosan változik. Természetesen az ilyenkor szokásos elvet követve, vagyis a felületet olyan felületelemekre osztva, amelyen belül a nyomás állandónak vehető, az ezen felületelemekre ható erők meghatározhatók, és összegzésükkel az edény oldalfalára ható erő nagysága általában kiszámítható. Az így adódó erő tehát az a koncentrált erő, amellyel a folyadéknyomásból származó erőrendszer helyettesíthető, azaz a megoszló erőrendszer eredője.

Említettük, hogy a Föld gravitációs terében elhelyezkedő kis kiterjedésű folyadéktér elemeire ható súlyerők jó közelítéssel párhuzamosak és a földfelszínre merőlegesek, így mondhatjuk, hogy a nehézségi erőtér hatása alatt álló folyadéktérben a nyomás egy vízszintes felület minden pontjában egyenlő. Azokat az edényeket vagy edényrendszereket, melyek között a folyadék vagy gáz szabadon áramolhat, közlekedő edényeknek nevezzük, és előbbi megállapításunk kapcsán megfogalmazhatjuk a közlekedőedény elvet:

Közlekedőedények száraiban az edény aljától számított ugyanazon magasságban a nyomások egyenlők, ha az egyenlő magasságban lévő pontok még ugyanabban a folyadékban vannak.

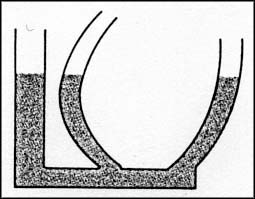
Ezt az elvet egyes hidrosztatikai feladatok megoldásánál gyakran alkalmazzuk, ügyelnünk kell azonban arra, hogy a kiválasztott szintfelület ugyanabban a folyadékban legyen.

Hidrosztatikai felhajtóerő Archimedes-törvénye:

a folyadékba mártott testre felhajtóerő hat, amely nagyságra nézve egyenlő a test által kiszorított folyadék súlyával 

F_fel r_fVg

F F₁ = r_fg(h₂ h₂)q = r_fgV

A felhajtóerő támadáspontja a test által kiszorított folyadék súlypontja. 

Súlyos folyadék és szilárd test egyensúlya: Arkhimédesz törvénye

Tapasztalatból tudjuk, hogy a folyadékba helyezett szilárd test egyes esetekben elmerül, más esetekben a folyadékba teljesen bemerülve a folyadék belsejében bárhol egyensúlyi helyzetben marad, vagyis lebeg, míg olyan esetek is előfordulnak, amelyekben a test a folyadékba részlegesen bemerülve annak felszínén úszik.

Az egyensúlyban lévő testre ható erők eredőjének természetesen zérusnak kell lennie, ami csak úgy teljesülhet, ha a folyadék valamely felfelé irányuló, a testre ható erő kifejtésével a test súlyerejével egyensúlyt tart. Ezt, a folyadék nyomásából származó, a folyadékba merülő testre felfelé ható erőt felhajtóerőnek nevezzük.

A felhajtóerő nagyságának meghatározásához végezzünk el egy egyszerű gondolatkísérletet!

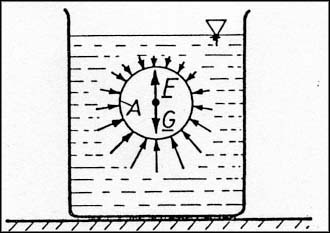
Jelöljünk ki az ábrán vázolt folyadéktérből egy A zárt felülettel körülhatárolt térrészt! Ez a folyadéktérrész egyensúlyban van, vagyis a folyadéknyomásból származó megoszló erőrendszer eredője egyensúlyt tart a térrészben lévő folyadék súlyerejével:

.

Amennyiben a folyadéktérrészt kiemeljük és helyére egy vele megegyező szilárd testet helyezünk, a folyadéknyomásból származó megoszló erőrendszer eredője nem változik, vagyis erre a szilárd testre is a kiszorított folyadék súlyerejével megegyező nagyságú, felfelé mutató erő, a felhajtóerő hat. Ezek alapján megfogalmazhatjuk tehát Arkhimédesz törvényét:

Minden folyadékba merülő testre akkora felhajtóerő hat, amennyi a test által kiszorított folyadék súlya.

Azokban az esetekben, amikor a test súlyereje nagyobb a teljes bemerüléshez tartozó felhajtóerőnél, a test elsüllyed. A két erő egyenlősége esetén a test a folyadékban lebeg, akkor pedig, amikor a teljes bemerüléshez tartozó felhajtóerő nagyobb a test súlyerejénél, a test a folyadékba csak részlegesen merül, és a folyadék felszínén úszik.

A bemerülés mélységét természetesen ki tudjuk számítani, hiszen a kiszorított folyadék térfogata, amely a felhajtóerő nagyságát meghatározza, éppen egyenlő a test folyadékba merülő részének térfogatával, és az erők egyensúlyából a test folyadékba merülő térfogata, illetve abból a bemerülés mélysége meghatározható.

21. Nyugvó gázok mechanikája, légnyomás.

Pascal-törvénye: a nyugvó gáz, ha súlya elhanyagolható, az edény falára mindenütt  ugyanakkora nyomást fejt ki.  
 

A légköri nyomás (légnyomás)

Torricelli  (1608-1647) 

0 ^oC-on  

      p V = p₂V₂ = ... 

Boyle-Mariotte-törvény

meghatározott tömegű és állandó hőmérsékletű gáz nyomásának és térfogatának szorzata állandó 

      pV = állandó (ideális gázra) 
 

vagy  ρ = m/V  felhasználásával ,  vagy 

ahol  C, C' állandók

(anyagi minőségtől, tömegtől, hőmérséklettől függőek) 
 

Nyomás- és sűrűségeloszlás nehézségi erőtérben lévő gázokban

Δp = -ρgΔh 

Δh → 0  határesetben 

     barometrikus magasságformula 

A gázokra is érvényes Archimedes-törvénye: a gáz a benne lévő testekre felhajtóerőt gyakorol, amely akkora, mint a testtel egyenlő térfogatú gáz súlya 

F_fel = ρ_gázVg

A folyadékok és gázok mechanikája olyan adalékokat szolgáltathat, mint a légnyomás és mérése, a nyomás terjedése folyadékokban (alkalmazások említésével együtt), a különböző nyomás-mértékegységek kialakulásának története. A közlekedőedények törvénye különösen alkalmas arra, hogy kísérletileg bemutassuk és a tanult törvényekkel összefüggésbe hozzuk. Tudománytörténeti, de alkalmazásbeli jelentősége is van Arkhimédész törvénye tanulmányozásának is. A felhajtóerő jelenlétének kimutatása egyszerű kísérleti feladat, és jól felhasználható konkrét vizsgálódások elvégzésére is: annak megjósolása, hogy egy test úszni fog vagy elmerülni adott sűrűségű folyadékban, a szilárd testek sűrűségének meghatározása stb. Kiegészülhet olyan kitekintésekkel, mint a sarkköri jégtakaróról leszakadt tömbök úszása, olvadása, a felmelegedés problémakörének vázolása.

22. Folyadékok és gázok áramlása (az áramlások leírása; kontinuitási egyenlet; Bernoulli-féle egyenlet).

Az ideális folyadék áramlása. Bernoulli-féle egyenlet

Tapasztalatok:

- a házak között erősebben fúj a szél, mint a nyílt téren,

- a vízcsapból kifolyó víz elvékonyodik,

- az erős szélben megemelkednek a tető cserepei, stb.

Az ideális folyadék dinamikája, áramlástana úgy "beszél" a valódi folyékony és légnemű halmazállapotú testek mozgásáról, hogy a bennük működő erőket figyelmen kívül hagyja. Ez a leírása csak akkor alkalmazható, amikor a belső súrlódás valóságos esetekben elhanyagolhatóan kicsi.

Réteges áramlás. Bernoulli-féle egyenlet.

Def Réteges (lamináris) áramlás az olyan, amikor az áramló folyadék egymással párhuzamos vékony rétegekre osztható, amelyek egymás mellet különböző sebességgel mozognak.

Def Az áramerősség (jele: I', egysége: kg/s) a mechanikában leszármaztatott mennyiség, amelyet a tömeg és az idő hányadosaként ételmezünk. A technikában összenyomhatatlan folyadék (r=konst.) esetében a térfogat és az idő hányadosával van definiálva (jele: I, egysége: m³/s):

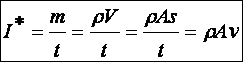(d4.13)

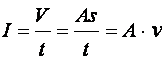
(d4.14)

Ideális folyadék áramlásának speciális esetei

Tétel: (Stacionárius áramlás változó keresztmetszetű fúvókákon = a kontinuitási egyenlet speciális esete) Változó keresztmetszetű vékony áramcsőben, összenyomhatatlan folyadék stacionárius áramlása esetén az áramerősség állandó:

(d4.15)

Tétel: (Bernoulli-féle egyenlet) Nehézségi erőtérben, súrlódásmentes, összenyomhatatlan folyadék, örvénymentes, stacionárius áramlása esetén a három nyomás dimenziójú tag összege az áramlási térben állandó:

(d4.16)

Súrlódó folyadék áramlása. Belső súrlódás. Hidrodinamikai ellenállás

Tapasztalatok

- kanalat nehezebb a mézből kihúzni, mint a vízből,

- folyóban a víz sebesség középen nagyobb, mint a széleken,

- a szélben lobog a zászló,

- a repülőgép merev szárnyakkal repül,

- lehet egyre áramvonalasabb autót és repülőgépet csinálni, stb.

Megjegyzések: Az előző tapasztalatokkal kapcsolatban a következő dinamikai magyarázat tehető:

- különböző sebességgel mozgó szomszédos folyadék részecskék egymásra súrlódási erőt gyakorolnak,

- a mozgó folyadékban jelentkező feszültség tagoknak sebesség jellegű mennyiségeknek kell lenni, ez lesz a deformációs sebesség

Def Réteges (lamináris) áramlás az olyan, amikor az áramló folyadék egymással párhuzamos vékony rétegekre osztható, amelyek egymás mellet különböző sebességgel mozognak.

Newton a folyadékok belsejében mozgás közben ható erőhatást, a belső súrlódást erőtörvény formában írta le (ez a Newton-féle súrlódási törvény), és ebben a formában értelmezte a súrlódási állandót. A belső súrlódást csak réteges áramlásnál értelmezzük. Ennek megfogalmazása a következő:

Def Belsõ súrlódásról áramló folyadékoknál akkor beszélünk, amikor az A felülettel szemben, egymástól z távolságban levő, u sebességgel egymáson elcsúszó rétegek között ható F erő a következő összefüggés szerint számolható. (ez a felfogás egyébként Newton-féle súrlódási törvényként ismert):

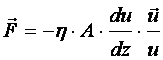(d4.17)

Ez összefüggés egyben a belső súrlódás jellemzésére alkalmazható anyagállandót, az h-t arányossági tényezőként tartalmazza.

Def.: A belső súrlódást (jele: h) csak réteges áramlásnál értelmezzük. Az h anyagállandó, amelynek a mértékegysége (N m^-2 s), azaz Pa s (pascal secundum).

Tétel: Réteges áramlás csőben: (Hagen-Poiseuille-féle törvény, 1839) (Ohm-törvény alakban megfogalmazva) Összenyomhatatlan, súrlódó folyadék, stacionárius áramlásakor, kör keresztmetszetű csőben (sugara: R, hossza: l) az áramerősség (I=V/t) a nyomástól (p) a következő összefüggés szerint függ:

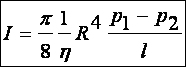
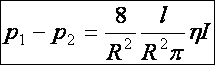U=R I (d4.18)

Megjegyzés: Ennek a törvényszerűségnek gyakorlati szerepe mind a vízvezetékek, mind pedig az erek mészkövesedése során bekövetkezett keresztmetszet változásában van.

Def Gomolygó (turbulens) áramlás az olyan, amikor

- az áramlás nem stacionárius, a sebesség és a nyomás egy meghatározott helyen nem állandó, hanem gyorsan ingadozik egy átlagérték körül,

- a folyadék részecskék pályái nemcsak, hogy nem egyenesek, nem is egyszerű görbék, hanem igen bonyolult módon egymásba fonódnak, a folyadék erősen összekeveredett,

- a cső végén az időegység alatt kiáramló folyadék térfogat sokkal kisebb, mint ami a p₁-p₂ nyomáskülönbség mellett a Hagen-Poiseuille törvény szerint adódna,

- a turbulens áramlásnál a cső "ellenállása" nagyobb, a folyadék viszkozitása látszólag megnövekedett.

Tétel: (Hidrodinamikai ellenállás) Ha egy összenyomhatatlan súrlódó folyadékban, amelynek r a sűrűsége, bármely A homlokfelületű test, olyan v sebességgel mozog, hogy a 10³ < Re < 10⁵ feltétel teljesül, a folyadék közegellenállását következő kifejezés adja meg:

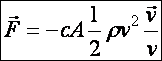(d4.19)

Tétel: (Reynolds-féle kifejezés, 1883) (jele: Re) A lamináris és a turbulens áramlások jellemzésére szolgáló egyik kifejezés a Reynolds-féle, amely a következőképpen írható fel:

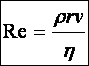(d4.20)

Megjegyzések: A Reynolds-féle kifejezés kritikus értéke, Re_k=1160. Ha egy áramlás során Re < Re_k, akkor az áramlás lamináris formája a stabilis, de ha Re > Re_k, akkor pedig a turbulens forma a stabilis. Egy folyadék teljes ellenállását úgy értelmezzük, mint a súrlódási és az un. nyomási ellenállás összege.

Tétel: (Hidrodinamikai hasonlóság) Dinamikailag hasonló áramlásokhoz ugyanaz a Reynolds-féle szám tartozik:

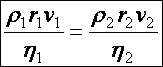(d4.21)

Megjegyzések: Létezik az ún. Kármán-féle örvényút, ahol az örvények periódikusan és szimmetrikusan válnak le (Kármán Tódor, 1911). Prandtl-féle határréteg tétel: A folyadék viszkozitását csak a szilárd testet körülvevő vékony "határrétegben" kell tekintetbe venni, a szilárd testtől nagyobb távolságban a súrlódásmentes folyadékok hidrodinamikája alkalmazható.

Kontinuitási egyenlet

A Wikipédiából, a szabad lexikonból.

Ugrás: navigáció, keresés

A kontinuitási egyenlet minden alábbi példája ugyanazt a gondolatot fejezi ki. A kontinuitási egyenletek a megmaradási törvények (erősebb) lokális kifejezései.

Elektromágneses elmélet

Az elektrodinamikában a kontinuitási egyenlet két Maxwell-egyenletből vezethető le. Azt fejezi ki, hogy az áramsűrűség divergenciája egyenlő a töltéssűrűség változási sebességének mínusz egyszeresével:

Származtatás

Az egyik Maxwell-egyenlet szerint:

Mindkét oldal divergenciáját véve:

,

de egy rotáció divergenciája nulla:

Egy másik Maxwell-egyenlet szerint:

Helyettesítsük ezt be az (1) egyenletbe:

ami a kontinuitási egyenlet.

Interpretáció

Az áramsűrűség a töltéssűrűség mozgása. A kontinuitási egyenlet szerint ha töltés távozik egy infinitezimális térfogatból (azaz a töltéssűrűség divergenciája pozitív), akkor a töltés mennyisége a térfogatban csökken. Ezért a kontinuitási egyenlet az elektromos töltésmegmaradás kifejezése.

Hidrodinamika

A hidrodinamikában a kontinuitási egyenlet a tömegmegmaradás kifejezése. Differenciális alakban:

ahol ρ a sűrűség, t az idő, és u a folyadéksebesség.

Kvantummechanika

A kvantummechanikában a valószínűség megmaradása szintén 'kontinuitási egyenlethez vezet. Legyen P(x, t) a valószínűségsűrűség, amivel:

ahol J a valószínűségi áram.

23. A hullám fogalma. A síkhullám matematikai alakja.

A hullám fogalma és leírása

A hullám valamilyen (mechanikai, elektromágneses, termikus, stb.) zavar térbeli

tovaterjedése. Terjedésének mechanizmusa függ a zavar jellegétől, így például a mechanikai

deformáció az anyag részei közti rugalmas kapcsolatok miatt terjed, az elektromágneses zavar

terjedése a változó mágneses- és elektromos tér egymást létrehozó hatásán alapul, a termikus

zavar terjedésének oka az anyag hővezetése, stb.

A harmonikus síkhullám matematikai alakja

y(t) = Asin( t)

ahol y(t) a pillanatérték az idő függvényében, A az amplitúdó, a körfrekvencia [rad/sec]-ban,

továbbá:

f

ahol f a frekvencia Hz -ben.

A harmonikus rezgőmozgást, mivel egyetlen f frekvencia alkotja, "tiszta" hangnak, vagy szinuszos

rezgésnek is nevezzük. Ilyen a természetben nem fordul elő, ezek mesterséges hangok.

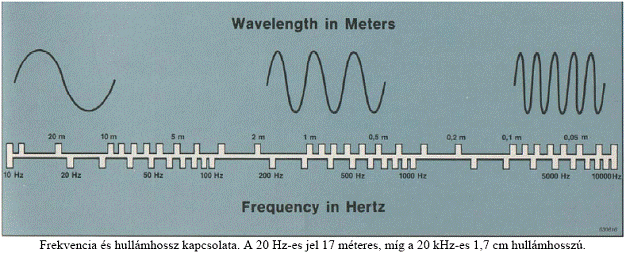
Egy szinuszos rezgésnek a frekvenciája megadja a másodpercenkénti rezgések számát, tehát az

1000 Hz-es hang másodpercenként pontosan ezer periódust tartalmaz. A Hz megadható 1/s alakban

is. Az amplitúdó a maximális kitérés értéke, amikor a sin( t) értéke 1 ill. -1. A rezgésnek van

fázisa is, amely a környezethez vagy más rezgésekhez való időviszonyt fejezi ki; más néven a

függvény értéke a t=0 időpillanatban.

Az általános alak:

y(t) = A +Asin( t+

ahol A az amplitúdó egyenszintje. Levegőben történő hanghullámterjedés esetén ez maga az

atmoszféranyomás, értéke A [Pa] = 1 [atm]. Ebből is látható már, hogy a hanghullámoknál az

amplitúdó a hangnyomásnak felel meg, de ez az általános leírás használható a hangszóró kapcsaira

adott feszültségnél is, akkor azonban Volt dimenziójú. A számításoknál ezt az értéket nem szoktuk

figyelembe venni, hiszen ez egy DC nyomásérték, amire legtöbbször nincs szükségünk, csak az erre

rászuperponálódó változásra. Az atmoszféranyomás a levegő paramétereitől, időjárástól, tengerszint

feletti magasságtól függ, de egy mikrofon átviteli függvényének megállapításához

egyszerűsíthetünk vele. Ez az 1 atmoszféra kiegyenlítésre kerül a fülben is "ellennyomás"

segítségével, amikor kinyitjuk a szánkat vagy nyelünk. Ha magas hegyre gyorsan megyünk fel,

akkor nincs elég idő a szabályozásra és bedugul a fülünk, mert a belső nyomás még az alsó nagyobb

értéken van, és ez kifelé nyomja a dobhártyát. Mivel nyeléskor nyílik a nyomáskiegyenlítő nyílás a

fülben (az ún. Eustach-kürt), néhány erősebb nyelés, cukorkaszopogatás ill. a nyitott szájjal való

utazás megelőzheti a füldugulást.

24. Hullámterjedés (hullámok törése). Huygens- és Huygens−Fresnel-féle elv.

Huygens elv

A hullámfront minden pontja új elemi hullámok kiindulópontja.

Új hullámfront Þ burkoló görbe

Példa

Feltételezés: a hátrafelé haladó hullámok burkolóját nem kell figyelembe venni (ezt egyszerûen kimondja az elv, mivel csak így magyarázható, hogy nem terjed a hullám visszafelé is.)

s¢-n megismételve az elõzõ szerkesztést, újabb burkoló szerkeszthetõ s². Itt van a hullámfront a t+2Dt idõpontban.

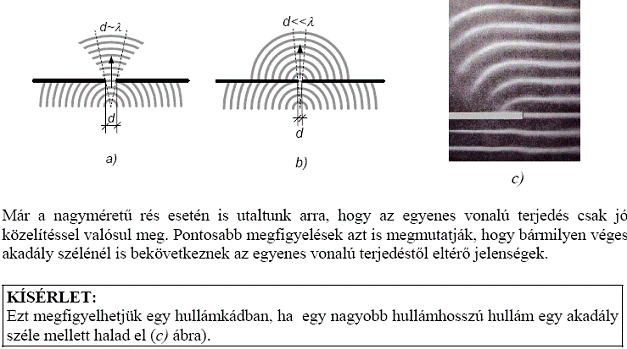
25. A hang és terjedése. A hangérzet jellemzői. Az emberi fül.

Longitudinális mechanikai rezgés. Terjedése közeghez kötött.

Jellemzői:

Frekvencia: ez határozza meg a hang magasságát. A magasabb hangok nagyobb, a mélyebb hangok kisebb frekvenciájúak.

A hallható hangok 16-20000 Hz frekvenciájúak. Az egyes embereknél ettől kisebb eltérések megfigyelhetők. (Ez a tartomány az életkorral is változik, idősebb korban a magasabb hangokat nem halljuk.)

A fül az inger frekvenciájának növelésére nagy frekvenciáknál nem reagál lineárisan, minél magasabb a hang, annál kevésbé érzékeljük a frekvencia különbségeket.

Zenei hangok: rezgésszámai nem folytonosan oszlanak meg, hanem bizonyos rezgésszámok arányában. A jó hallású ember a rezgésszámok aránya iránt érzékeny. Egyetlen hang rezgésszámát (abszolút magasságát) kevés ember képes érzékelni. (Az A hang rezgésszáma: 440 Hz)

Hangköznek két hang frekvenciájának arányát nevezzük.

Pl.: 1 oktáv: f₁/f₂ = 2

Infrahangok: f<16 HZ : kisebb-nagyobb tartományát néhány állatfaj képes érzékelni. A szívfrekvencia közelében (<3Hz) az infrahangok életveszélyesek (az érfalak megrepedését - belső vérzéseket okozhat).

Ultrahangok: f>20000 Hz . Néhány élőlény érzékeli. A delfinek, denevérek ennek segítségével tájékozódnak. Felhasználása: távolságmérés, orvosi diagnosztika, gyógyítás, kőzúzás, hegesztés, galvanizálás, köd és füst szétoszlatás stb.

Hangerősség: a rezgés amplitúdójától függ, mérésére többféle fizikai mennyiség is használatos: Hangintenzitás (I), a hangforrás által 1m²-nyi felületre kisugárzott teljesítmény.

Hangintenzitásszint: a fül elképesztően széles hangerő tartományt képes érzékelni, ezért a hangerő mérésére logaritmikus skálát használunk (dB). A hangintenzitás alapszintjének I₀ = 10^-12 W/m² -t vesszük (ez a már hallható leggyengébb hang) , a hangintenzitás szintjét a 10 lgI/I₀ értékkel adjuk meg dB-ben.

pl.            

I₁/I₂ decibel

1 0

5 7

10 10

50 17

100 20

500 27

1000 30

10¹⁰ 100

A 30 dB-nél erősebb hangokat már zajnak érzékelünk. 40-65 dB már fáradtságot okoz, 80 dB felett átmeneti hallásromlás áll be, (ilyen erős hangokra a hallócsontokat izmok feszítik meg, így gyengíti szervezetünk ezek érzését). 90 dB felett fülkárosodás következhet be. 120 dB a fájdalomküszöb. 170 dB körül a dobhártya megreped, 175 dB felett halálos a hang.

Az emberi fül a különböző frekvenciájú, azonos intenzitású hangokat nem azonos erősségűnek érzi. A hangerősség szubjektív megfelelője a hangosság, melynek mértékegysége a fon - a hangérzet nagyságának kifejezője. Használnak más skálát is, ahol a mértékegység a son.

(A hangerősség mérésére használhatjuk a hangnyomást, mely a dB-hez hasonló logaritmikus skálán is mérhető- hangnyomásszint)

Hangszín: a különböző erejű és magasságú hangok összeadódása. Zenében az alap és a felharmonikus hangok viszonylagos erőssége alapján a hangszer felismerhető. A hang színezetét pl. sípoknál a síp anyaga, alakja befolyásolja.

A nyomáshullámot az emberi fül alakítja idegi impulzusokká, ebbõl keletkezik az agyban a hangérzet. Az átalakítás hangintenzitás- és frekvenciafüggõ. Miután a fülünk érzékenysége emberenként más és más, egészséges átlagemberrel számolunk. A 10^-12-1 W/m² hangintenzitás között tartományt hívjuk hallható hangnak. Az ennél kisebbet küszöb alatti-, a nagyobbat szuperhangnak nevezzük.

A hallható hang frekvenciatartománya 20Hz-20 kHz között van, a kisebb frekvenciát infra-, a nagyobbat ultra-, majd hiperhangnak nevezzük [2]

A hang frekvenciája a hang magasságának felel meg, az alacsony frekvenciájú hangok a mélyek, a magas hangok frekvenciája pedig nagy. (A normál zenei "a" hang frekvenciája 440Hz, azaz ez a hang 440-et rezeg másodpercenként. Az ez alatt lévõ "c" hang frekvenciája, vagy rezgésszáma pedig 256 Hz. A "magas c" frekvenciája kétszer akkora, 512Hz, a "magas a" pedig 880Hz. Azaz egy oktávnyi ugrás kétszer akkor frekvenciának felel meg, két oktávnyi ugrás négyszer akkora frekvenciának, és 1024-szer akkora frekvencia 10 oktávnyi ugrásnak felel meg.)

külső fül

A külső fülhöz, tartozik a csontos és porcos fülkagyló (meatus acusticus externus et internus) és a külső hallójárat, amelynek belső végén a dobhártya (membrana tympani) feszül ki.

középfül

A középfülhöz, tartozik a dobüreg és annak melléküregei, a hallócsontok (kalapács (malleus), üllő (incus), kengyel (stapes)) és a fülkürt (tuba auditiva Eustachii). A külső és a középső fület a dobhártya választja el egymástól, ehhez van hozzánőve a kalapács nyele, amelyehez az üllő, ehhez pedig a kengyel kapcsolódik; ezek a csontok közvetítik a dohártya hanghullámok okozta rezgéseit a belsőfülhöz. A fülkürt (tuba auditiva) összeköti a dobüreget az orrgaratüreggel, és a fülkürtön át nyeléskor levegő juthat a dobüregbe.

belső fül

A belső fül a csontos tokból (csontos labirintus, labyrinthus osseus) és az abban helyet foglaló hártyás labirintusból (labyrinthus membranaceus) áll. A labirintus részei: a tér három síkjában fekvő félkörös ívjáratok (doctus semicrircularis), amelyekben az egyensúlyozási idegi végkészülékei foglalnak helyet, a tornác (vestibulum) és a csiga (cochlea). Ez utóbbiban a hallás idegvégkészüléke: a Corti-féle szerv található. A belső fülből indul ki a VIII agyideg (nervus acusticus), amely a hallás és egyensúlyozás ingereit továbbítja az agy megfelelő részeihez.

26. Fénytani alapfogalmak, a fény terjedési sebességének mérése.

A fény egy elektromágneses sugárzás, melynek hullámhossza az emberi szem által látható tartományba, azaz az infravörös és az ultraibolya közé esik. A három alapvető mennyiség, amely meghatározza a fényt (és bármely elektromágneses hullámot):

- Intenzitás (vagy amplitúdó, amelyet az ember a fényerőként, fényességként érzékel),

- Frekvencia (vagy hullámhossz, amelyet az ember színként érzékel),

- Polarizáció (vagyis a rezgés iránya, ezt az ember normál körülmények között nem érzékeli, csak a rovarok egy része).

A részecskéket a kvantum mechanika a fény kvantumainak, fotonoknak nevezi. A fotonok olyan részecskék, amelyek nyugalmi tömege zérus, így csak fénysebességgel mozoghatnak.

A fényspektrum színei

A fény sebességét úgy számoljuk ki, hogy a frekvenciáját összeszorozzuk a hullámhosszal:

c = f ×

Mivel a fény sebessége vákuumban állandó, ezért a látható fényt hullámhosszával is jellemezhetjük, 400 és 800 nanométer (nm) közé esik a látható fény hullámhossza.

A fény sebességének mérése:

A fény sebességét több fizikus is próbálta megmérni, köztük Bay Zoltán magyar fizikus is. Bay javaslata alapján a méter definícióját a fénysebesség és az időegységre vetítik vissza, így a fénysebesség értéke a méter definíciója alapján pontosan m/s. Azaz a fény 1m-t körübelül 1/300 000 másodperc alatt tesz meg.

A fénysebességet sokszor sokan megmérték. Először Galilei próbálta a fény sebességét megmérni két távoli hegycsúcson lámpák segítségével. A kísérletben először Galilei nyitotta ki a lámpást, és amikor segítője meglátta a fényt, ő nyitotta ki. Galilei rájött, hogy a reakcióidő jelentős részét teszi ki a mérésnek, felhagyott a kísérletezéssel.

Az egyik legkorább értékelhető mérést a dán fizikus Ole Romer 1676-ban végezte. A Jupiter egyik holdját, az Iot figyelte, és eltéréseket vett észre az Io keringési periódusaiban. Romer az eltérésekből 227 000 Km/s-os értéket kapott a fénysebességre.

Az első sikeres mérés, amely csak földi tárgyakat használt Hippolyte Fizeau mérése volt 1849-ben. Fizeau fénysugarakat irányított egy több kilométerre lévő tükörre, és egy fogaskereket helyezett a fény útjába, melyen a fény oda-vissza áthaladt. Ha állt a kerék, a fény áthaladt a fogközön és ugyan ott vissza is jött. Ha forgott, átment a fogközön, de visszafele a fogra érkezett. Ha növelte a fordulatszámot, a fogon áthaladó fény a következő fogon jött vissza. Ha ismerjük a távolságot és a fordulatszámot, a fény sebessége kiszámolható. Ő akkor 313 000 Km/másodpercet kapott.

Albert A. Michelson 1926-ban forgó tükrök használatával korrigálta Romer mérését. A precíz méréssel 299 796 Km/s-ot kapott. Hétköznapi használatban gyakran felkerekítjük 300 000 Km/s-ra.

27. A fénytörés és visszaverődés törvényei. A Fermat-elv és alkalmazása.

A Fermat elv kimondja, hogy két pont között a fénysugár azokon az utakon

halad, amelyek megtételéhez a legrövidebb idore van szüksége más útvonalakkal

szemben. A Snellius-Descartes törvény kimondja, hogy közeghatárra

érve a fény úgy törik meg, hogy a beeso illetve a visszavert fénysugarak

felületi normálissal bezárt szögeinek szinuszai úgy aránylanak egymáshoz,

mint a törofelület két oldalán lévo közegek törésmutatói.

n sin n sin

Ha a fénysugár optikailag surubb közegbol ritkább felé halad, eloállhat a

teljes visszaverodés esete, amikor a fény a közeghatárról visszaverodik. Ekkor

a tükrözodésre vonatkozó törvényszeruség érvényesül, mely szerint a beeso

illetve a visszaverodo sugár beesési pontba állított normálissal bezárt szöge

megegyezik, továbbá egy síkban helyezkednek el.

A fénytörés

Ha a fény valamely átlátszó közeg határára érkezik, mint azt az előzőkben láttuk, akkor onnan a fény egy része visszaverődik, másik része pedig behatol a közegbe. A részleges visszaverődés jelenségét, amit a francia fizikus, Augustin Fresnel (1788-1827) vizsgált behatóan, tükröződésnek, vagy Fresnel reflexiónak hívják. Fresnel értékes munkát végzett a fény hullámelméletének kidolgozásában, s megalkotta a róla elnevezett lencsét, melyet a világítótornyokban használnak. A tükröződéssel később még részletesebben foglalkozunk az átviteli veszteségek tárgyalásakor.Zárjon be a beeső fénysugár a felület normálisával alfa szöget! Ha a fénysugár nem merőlegesen érkezik, azaz ha a beesési szög különbözik zérustól, a közegbe behatoló fénysugár haladási iránya megváltozik, és a beesési pontban a felületre bocsátott merőlegessel, a beesési merőlegessel béta szöget bezárva folytatja útját.


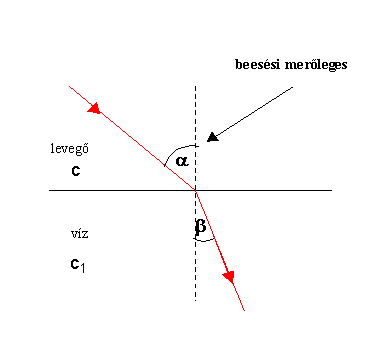
beesési és törési szögek közötti összefüggést Wilebrod Snell van Roinen (latinosan Snellius) (1591-1626) fedezte fel 1621-ben. Megállapította, hogy nem a szögekre, hanem azok szinuszaira mondható ki a törési törvény, melynek elméleti kidolgozásából René Descartes (1596-1650) is kivette a részét. A fénytörés törvényét ezért Snellius-Descartes féle törvénynek nevezzük, miszerint a beesési szög és a törési szög szinuszának hányadosa állandó. Ezt az állandót a közeg törésmutatójának (angolul index) nevezzük:

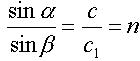
A fénytörés oka az, hogy a fény a különböző közegekben különböző sebességgel terjed. Mint ismeretes, a fény vákuumban másodpercenként mintegy 300 ezer kilométert tesz meg. (A vákuumbeli fénysebesség szokásos jelölése c.) Ha a fény valamely átlátszó közegbe jut, abban kisebb, mondjuk c1 sebességgel tud csak haladni. Ezért azt is szokták mondani, hogy a közeg optikailag sűrűbb, mint a vákuum. Az n=c/c₁ hányadost az illető közeg vákuumra vonatkoztatott törésmutatójának nevezzük. A víz törésmutatója pl. n=1,33, mivel abban a fény csak 225 ezer km/s-os sebességgel halad.

28. A teljes visszaverődés. A fényvezető szálak működése.

A teljes visszaverődés

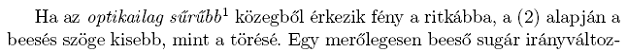
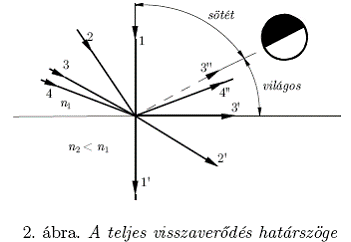
Ha a fény az optikailag ritkább közegből (pl. levegő) lép át a sűrűbbe (pl. víz), mint azt az ábrán a balról jobbra mutató egyszeresen nyilazott fénysugár mutatja, a törési szög mindig kisebb lesz a beesési szögnél . Ha most a beesési szöget egészen 90 fokig növeljük (ld. kétszeresen nyilazott sugár), a törési szöggel elérkezünk egy határig, a sin(90⁰) = 1 miatt:

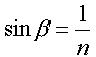
A közegbe belépő fénysugár ennél nagyobb szöget nem zárhat be a beesési merőlegessel. Fordítsuk most meg képzeletben a fénysugár haladási irányát, és érkezzen a fény az optikailag sűrűbb közegből (ld. jobbról balra mutató nyilak) a beesési merőlegestől egyre nagyobb szög alatt! A törési törvény most is érvényben marad mindaddig, amíg a beesési szög növelésével a b' határszöget el nem érjük, mikor is a kilépő fénysugár mintegy "súrolja" a közeg felszínét. A béta szöget ugyan most minden akadály nélkül tovább növelhetjük (balra mutató háromszoros nyíl), de a fény többé már nem tud kilépni a közegből, hanem ilyenkor a határfelületen teljes visszaverődést szenved (Kepler, 1611). A szöget ezért a teljes visszaverődés határszögének nevezzük A fényvezető szálak ezt a természettörvényt használják ki a fény csapdába ejtéséhez.

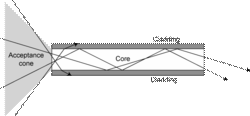
Az optikai szál egy hengeres szigetelt könnyen hajlítható szál, ami fényt továbbít az üvegmag belsejében, a teljes fényvisszaverődés elve alapján. A szál áll egy üvegmagból amit körül vesz egy védő réteg amit héjnak nevezünk. Hogy a teljes fényvisszaverődés benntartsa az optikai jelet a magban, a mag törésmutatójának nagyobbnak kell lennie mint a héjnak. A határ a mag és a védő réteg között vagy hirtelen, mint a egymódusú szálnál, vagy fokozatos, mint a multimódusú szál esetében. A nagy magátmérőjű szálat multi-módusú szálnak, az elektromágneses analízis alapján (lásd lejjebb). A bevezetett fénysugarak a mag belsőfalán tengelyének irányában végig halad a teljes visszaverődés hatására. A mag és védőréteg határához nagy szögben érkező sugarak (a határhoz párhuzamosan húzott vonalhoz képest nagy szögben) teljesen visszaverődnek. A teljes visszaverődés által meghatározott visszaverődési határszöget (a legkisebb szög amelynél a fénysugár még teljes mértékben visszaverődik) az üvegmag és a héj anyagainak törésmutatókülönbsége határozza meg. A kis szögben érkező sugarak átlépnek az üvegmagból a héjba, ahol már nem tudnak végighaladni, elvesznek a héjban. Ebben az esetben, a visszaverődési határszög meghatározza a szál befogadó szögét, amit gyakran numerikus apertúrának neveznek. A magas numerikus apertúrával rendelkező optikai szálat könnyebben lehet csatlakoztatni az optikai vevőhöz vagy adóhoz. Azonban, azzal hogy megengedjük a fénysugárnak, hogy több fénysugárként haladjon a szálban és ezzel különböző szögekben terjedjenek a sugarak, a nagy numerikus apertúra szintén növeli a bejárt utak számát, és ezzel a szórást (diszperziót), azaz azt, hogy az egyes utakon terjedő jelek különböző idő alatt érnek a szálvágre.

29. Az optikai kép fogalma. Optikai leképezés gömbfelületen való törés útján.

Egy pontszerû tárgyat közvetlenül látunk, ha a róla kiinduló fénysugarak úgy jutnak a szemünkbe, hogy közben nem változtatják meg az irányukat. A pontról kiinduló fénysugarakat szemünk az ideghártya egy pontjába gyûjti össze, agyunk a pont helyét pedig - a fénysugarak megfordíthatósága alapján - ott látja, ahol az eredetileg széttartó (divergens) nyaláb egyesülni látszik. Agyunknak ez a tulajdonsága akkor érdekes, ha a pontról kiinduló fénysugarak valamilyen irányváltozást szenvednek, például egy tükörrõl visszaverõdve jutnak a szemünkbe. Ekkor a pont helyét újra csak a közvetlenül a szemünkbe jutó fénysugár alapján határozzuk meg, vagyis annak az iránynak a meghosszabbításában látjuk, amely irányból a fény a szemünkbe lépett. Ez természetesen sok esetben téves észleléshez vezet A vizsgált folyamatban a tárgypontról kiinduló fénysugarak két különbözõ módon alkotnak képet. Az egyik esetben (a retinánkon) a fénysugarak valóban egyesülnek, ezt a pont valódi képének nevezzük. Az a pont, amelyben a fénysugarak a tükör mögött egyesülni látszanak, a pont látszólagos képe.

Elnevezések: a gömbtükrök O geometriai középpontja megegyezik annak a gömbnek a középpontjával, amely részének e tükör tekinthetõ. A gömbtükör C optikai középpontja a tükrözõ felület középpontja. Az optikai középpont és a geometriai középpontra illeszkedõ egyenes a gömbtükör optikai tengelye. A tükör nyílásszögét a geometriai középpontot a tükör széleivel összekötõ egyenesek által bezárt szöggel jellemezhetjük.

A gömbtükrök esetén négy olyan speciális sugármenet van, amelyek mindig azonos, könnyen reprodukálható visszaverõdést szenvednek:

1. Az optikai tengellyel párhuzamos sugarak a fókuszponton haladnak át. (Domború tükörnél a sugaraknak a tükör mögötti meghosszabbításai mennek át a fókuszon.)
2. Az optikai középpontba futó sugarak a visszaverõdésük után ugyanakkora szöget zárnak be az optikai tengellyel, mint a beeséskor.
3. A fókuszponton áthaladó sugarak az optikai tengellyel párhuzamosan verõdnek vissza. (Domború tükörnél az olyan sugarak verõdnek vissza az optikai tengellyel párhuzamosan, amelyek tükör mögötti meghosszabbításai átmennek a fókuszon.)

A geometriai középponton átmenõ sugarak önmagukban verõdnek vissza. (Domború tükörnél azok a sugarak verõdnek önmagukban vissza, amelyeknek a tükör mögötti meghosszabbításai átmennek a geometriai középponton.)
A domború gömbtükör esetén a tárgy bármely helyzetében kicsinyített, egyenes állású, látszólagos kép keletkezik.A homorú tükrök képalkotásának jellegzetes esetei:

30. Lencsék (lencseegyenlet) tárgyalása a legrövidebb idő elve alapján.

Lencsék képalkotása

A kép megszerkesztéséhez három nevezetes sugármenetet használnak fel, amelyek egyúttal három fontos pontot is meghatároznak. 

1) A főtengellyel párhuzamosan beeső sugár törés után a képoldali fókuszponton (F) megy át (szórólencse esetén úgy megy tovább, mintha a fókuszból érkezne).

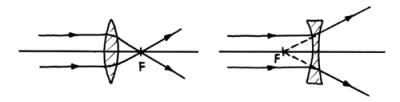
Ez a szabály a lencseegyenletből is megkapható: Párhuzamos sugarak végtelenben lévő tárgyról érkeznek, tehát t = . Behelyettesítve azt kapjuk, hogy k = f , azaz a kép a lencsétől f távolságban, a fókuszpontban keletkezik.

2) A tárgyoldali fókuszponton (F') át beeső (szórólencsénél a fókuszpont felé tartó) sugár törés után a főtengellyel párhuzamos lesz.

Ez a lencseegyenletben azt jelenti, hogy a lencsétől f távolságban, a tárgyoldali fókuszpontban elhelyezett tárgy képe (t = f) a végtelenben keletkezik (k = ).

3) A lencse csomópontján (K) átmenő sugár nem változtat irányt. A csomópont vékonylencsék esetén a lencse középpontja.

31. Nevezetes sugármenetek, lencseegyenlet.

Optikai lencsét kapunk, ha átlátszó anyagból (általában üvegből vagy műanyagból) két gömb-, vagy egy gömb- és egy síkfelülettel határolt darabot vágunk ki. Alapvetően a lencséket két csoportba soroljuk: domború és homorú lencsékre.

A domború lencsék azok, amelyek középen vastagabbak, mint a szélüknél. A domború lencsét (amennyiben a lencse anyaga optikailag sűrűbb, mint a környezete), gyűjtőlencsének is nevezzük.
A homorú lencsék (szórólencsék) a szélükön vastagabbak.

A lencsék képalkotásakor - ha a leképezési hibáktól eltekintünk - a tárgy egyes pontjaiból kiinduló és a lencsén áthaladó valamennyi fénysugár vagy valóságosan, vagy látszólagosan egy-egy ponton (az úgynevezett képpontokon) halad át. A kép megszerkesztésének bemutatásakor ezért elegendő néhány nevezetes sugármenetet kiválasztani.

Optikai tengelynek nevezzük a lencsét határoló két gömb középpontját összekötő egyenest. Az optikai tengelynek a lencse fősíkjával vett metszéspontja a lencse középpontja.

Nevezetes sugármenetek:

A lencsére az optikai tengellyel párhuzamosan eső fénysugarak a gyűjtőlencse esetén a lencse után az optikai tengelyen metszik egymást. Ezt a pontot gyújtópontnak vagy fókuszpontnak nevezzük. A nevezetes sugármenetek Szórólencse esetén az optikai tengellyel párhuzamos sugarak széttartóvá válnak, mintha a lencse előtt, az optikai tengelyen levő pontból indultak volna ki. Ezt a pontot (a szórólencse fókuszpontját) úgy kapjuk meg, hogy a széttartó fénysugarakat a tárgy felőli oldal irányába meghosszabbítjuk.

A fénysugár megfordíthatósága miatt igaz, hogy azok a fénysugarak, amelyek a lencse fókuszpontján át esnek a lencsére, az azon való áthaladás után az optikai tengellyel párhuzamosan haladnak tovább. Azok a fénysugarak, amelyek a lencse középpontján haladnak át, irányváltoztatás nélkül folytatják az útjukat.

A fókuszpont és az optikai középpont közötti távolság a fókusztávolság (f). Az előbbiek alapján a domború lencséknél valódi, a homorú lencséknél látszólagos (virtuális) fókuszról beszélünk. A számítások során ezért a domború lencsék fókusztávolságát pozitív, a homorú lencsék fókusztávolságát negatív előjellel vesszük figyelembe.

Képszerkesztés a nevezetes sugármenetekkel:

3.4.1. A domború lencse képalkotása

Helyezzük el az optikai tengelyre merőlegesen egy T tárgyat, amelynek az egyszerűség érdekében tekintsünk el az optikai tengelyen mérhető kiterjedésétől! Mivel a tárgynak az optikai tengelyen álló alappontjának képe is az optikai tengelyre esik, és - amint az könnyen ellenőrizhető - a kép is a tengelyre merőleges állású lesz, elegendő a tárgy csúcspontjának (a nyíl hegyének) képét megkeresni, a kép abból meghatározható.

Alkalmazzuk a következő elnevezéseket:

A tárgy és kép síkjának a lencse fősíkjától (egyszerűbben a tárgy és kép optikai tengelyen lévő pontjának a lencse középpontjától) mért távolságát tárgy- illetve képtávolságnak nevezzük.

A kísérletből megfigyelhetjük a kép helyének és méretének a tárgytávolságtól és a tárgy nagyságától való függését is.

A gyűjtőlencséket a gyakorlatban is alkalmazzák ezeknek a képeknek az előállítására. Az a. esetnek megfelelő leképezés jellemző például a fényképfelvételre, a c. eset a diavetítésre vagy a fénykép (papírkép) nagyításakor, az e. eset az, amikor a lencsét egyszerű nagyítóként használjuk. Természetesen az optikai eszközökben (vetítő, fényképezőgép, stb. ) a leképezési hibák kiküszöbölése érdekében nem egyetlen lencsét, hanem lencserendszereket alkalmaznak, de a leképezés elve nem változik.

32.Optikai leképezés gömbtükrökkel.

>>LAPOZZZ VISSZA!<<

33. A szem és a látás, a szem optikai hibáinak korrigálása.

A szem felépítése

A szem mint optikai rendszer

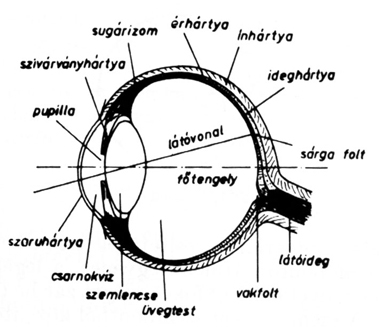
A szembe jutó fény négy határfelületen törik meg, amíg eljut a retinára. A határfelületek, és a hozzájuk tartozó törőerősségek (végtelenbe néző szem esetén) a következők:

A szem össz-törőereje tehát kb. 60 dioptria. A fény legnagyobb mértékben a levegő-szaruhártya határon törik meg. A lézeres szemműtétek során a szaruhártya felszínéről égetnek le egy réteget oly módon, hogy a szaruhártya feszínének görbületi sugara, így törőerőssége is épp a megfelelő mértékben változik meg.

Ahhoz, hogy a szem különböző távolságban lévő tárgyak képét egyaránt képes legyen a retinára fókuszálni, változtatnia kell törőerejét. Ezt a folyamatot hívják távolsági alkalmazkodásnak, vagy akkomodációnak.

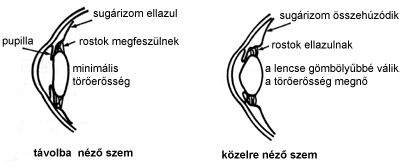
Akkomodáció során a lencse törőereje változik meg. A lencsét körülvevő sugárizmok összehúzódásakor a lencsét kifeszítő rostok elernyednek, a lencse domborúbb lesz. Ekkor főleg a szemlencse elülső felületének görbülete változik (kb. 10 mm-ről 6 mm-ig), nő a szemlencse átlagos törésmutatója is, így a szem törőereje kb. 60-ról 70 dioptriára nő.

A redukált szem

A szem optikai szempontból közelítőleg helyettesíthető a redukált szemmel (ábra), amely csak egy törőfelülettel rendelkezik; ennek görbületi sugara 5,1 mm, tetőpontja 2,3 mm-re a szaruhártyáé (S) mögött van. E felület K görbületi középpontja a redukált szem csomópontja: a K felé tartó összes sugarak K-n irányváltoztatás nélkül mennek át.

A retinán keletkező valódi kép kicsinyített és fordított. A képet az agy látóközpontja "fordítja meg". A szem érzékenysége

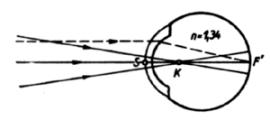
A szem bámulatosan széles fényerősség tartományban képes fényérzékelésre: az átfogott tartomány tíz nagyságrendnyi, azaz a minimális és a maximális intenzitás közötti szorzó 10.000.000.000.

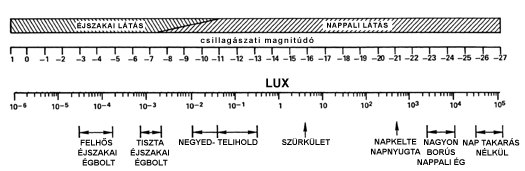
Képesek vagyunk látni ragyogó napfényben, de megfelelő körülmények között a szem akár 10 foton érzékelésére is képes. Ilyen nagyfokú érzékenységhez hozzászokásra, adaptációra van szükség. A teljes sötétadaptáció kb. 40 percet vesz igénybe. Adaptáció nélkül az érzékelt tartomány nagyjából 3 nagyságrendnyi.

Gyenge fényre nem a látógödör (fovea centralis), hanem a környezete a legérzékenyebb, mert itt található a legtöbb pálcika. Ezért könnyebb észrevenni egy halvány csillagot ha nem rá, hanem mellé nézünk. A csapsejtek színeket és finomabb részleteket érzékelnek.

A színérzékenységi görbe

Normális megvilágítás mellett az emberi szem kb. a 400-700 nm közötti hullámhosszakat érzékeli, ekkor az 555 nm-es sárgászöld fényre a legérzékenyebb. Gyenge megvilágításnál az érzékelt tartomány kb. 380-tól 650 nm-ig terjed, 507 nm-nél található maximummal. Az alábbi ábra a színérzékenységi görbét ábrázolja, ahol a normális, a gyenge megvilágításhoz tartozik.

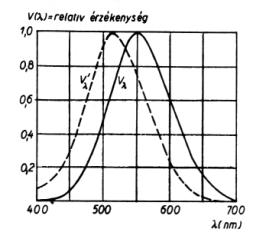
Mivel az UV tartományt főleg a lencse szűri ki, a lencse műtéti eltávolítása után az ember képes az UV tartomány egy részét látni. 

A szem színi felbontása 500 nm-nél 1 nm, a látható spektrum alsó részén kb. 6 nm.

A szem felbontóképessége (látásélesség)

Két pont különállónak látszik, ha a pontokból kiinduló, K-n áthaladó sugarak szöge kisebb mint a látásélesség határszöge amely 1' (1 ívperc). Ekkor 1 m távolságból szemmel "felbontható" két egymástól 0,3 mm-re lévő pont.   Kiszámítható, hogy ekkor a két kép a retinán mintegy 5 um-re van egymástól. Összevetve ezt a kb. 2 um-es receptorok közötti átlagos távolsággal, kiderül, hogy két pont akkor bontható fel, ha képük két olyan receptorra esik, amelyek között van egy harmadik, amely nem jön ingerületbe. A felbontóképesség ily módon függ a receptorok közötti távolságtól: legnagyobb a látógödörben (fovea centralis), mert itt maximális a receptorsűrűség.

A térbeli látás

Mindkét retinán alkotott kép sík! De mivel más perspektívájúak, az agy látóközpontja térhatású képpé egyesíti azokat. Fél szemmel a távolságok nehezen becsülhetők.   Ezt alkalmazzák a sztereomikroszkóp esetén. Térbeli hatás érhető el sík képekkel is, ha a képet a két szem nézőpontjának megfelelő két képből állítják össze, és megfelelő szűrőn át nézve mindegyik szem csak a neki szánt képet látja. A szűrőpár lehet vörös és zöld üveg, vagy két merőlegesen elhelyezett polarizátorból, ez utóbbit használják a 3D mozikban. Szemhibák, szemüvegek

A helyes látású szem akkomodáció nélkül a főtengellyel párhuzamos sugarakat a sárgafoltra fókuszálja. Tehát a legtávolabbi élesen látható pont, a távolpont a végtelenben van.   Ha a távolpont közeledik, azaz adott pontnál messzebb nem látunk élesen, rövidlátásról, myopiáról beszélünk. A rövidlátó szem a retina elé fókuszálja a képet. A legerősebb alkalmazkodás mellett élesen látható legközelebbi pont, a közelpont 10 éves korban kb. 7 cm, 30 éves korra kb. 15 cm, 60 éves korra kb. 80 cm. Ha a közelpont távolodik, távollátásról beszélünk. A távollátó szem a retina mögé fókuszálja a képet.

Öregkori látás (presbiopia) során a közelpont távolodik, főleg azért, mert a lencse rugalmassága csökken. Ha a távolpont eközben közeledik, bifokális szemüveget használnak.

A tiszta látás távolsága amelynél nem megerőltető alkalmazkodás mellett lehet olvasni, írni, 25 cm.

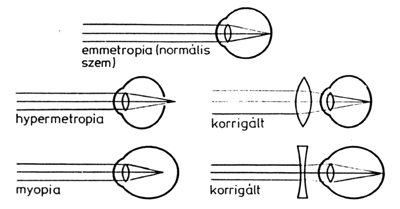
Asztigmatizmus esetén a szem az egymásra merőleges vonalakat nem látja egyszerre élesen. Az ok hogy a szem két egymásra merőleges síkban vett gyújtótávolsága különbözik. Hengerlencsés szemüveggel korrigálható.

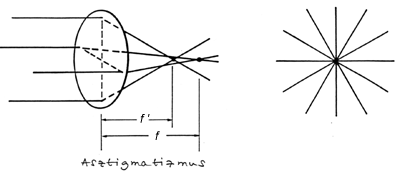
Kromatikus aberráció esetén a különböző színű fénysugarak más pontba fókuszálódnak. Szférikus abberráció esetén a főtengelytől különböző távolságban érkező sugarakra vett fókusztávolság különbözik.

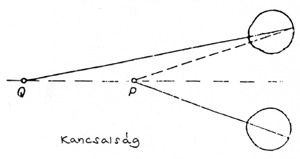
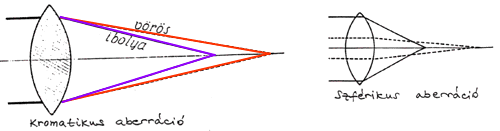
A kancsalság hibás szemállás. A két szem látóvonala nem ugyanabban a pontban metszi egymást, más pontokat látnak élesen.

34. Fontosabb optikai eszközök és működésük I: nagyító, fényképezőgépek/vetítők.

4.4. A szem és a fényképezõgép

Ha összehasonlítjuk az emberi szem és a fényképezõgépek felépítését, sok hasonló funkciójú, gyakran hasonló szerkezetû elemet is találunk. Ez valójában nem meglepõ, hiszen mindkét "eszköz" ugyanazt a szerepet látja el: különbözõ fényviszonyok mellett, különbözõ távolságban lévõ tárgyakról kell éles képet létrehoznia egy fényérzékeny felületen.

Ennek megfelelõen a közös építõelemek:

Természetesen a két szerkezet között lényeges különbségek is vannak. Az optikai leképezés azonban lényegében mégiscsak hasonlóan zajlik a két esetben.

4.4.1. A fényképezés

A fényképezés más néven FOTOGRÁFIA, képek megörökítése fénnyel fényérzékeny anyagon; a fotómûvészet mûalkotások létrehozása ilyen eljárással, ill. e mûvek összessége.

A fotográfia szó a görög photosz (fény) és graphein (rajzolni) szavakból származik. Elõször Sir John F. W. Herschel használta 1839-ben.

Fényképezéskor a fényképezõgép lencséivel képet vetítenek a gépben levõ filmre vagy lemezre. A film vagy a lemez cellulóz-acetátból, üvegbõl vagy más átlátszó anyagból van, és a felületét valamilyen ezüstsóval, például ezüst-kloriddal vagy ezüst-bromiddal képzett, fényérzékeny emulzió borítja. A megvilágítás (vagy exponálás) után a filmet kiveszik a fényképezõgépbõl, és elõhívó oldatba teszik. Ahol a filmet fény érte, finom eloszlású, fekete ezüstszemcsék jelennek meg. A legerõsebben megvilágított részeken válik ki a legtöbb ezüst. Az így keletkezõ negatívon fordítva mutatkozik a fény és az árnyék, mint a valóságban. Az ezüstöt kémiai úton, rendszerint nátrium-tioszulfát oldattal (fixír) rögzítik. Az exponálatlan ezüstsót további vegyszerekkel oldják fel, és vízzel mossák ki.
A pozitív képet - a fényképet - fényérzékeny papírra másolják át a negatívról. A negatívot a papír fölé teszik és megvilágítják. A legvilágosabb részek engedik át a legtöbb fényt, ezért a másolaton a negatív kép fordítottja látható. A jó minõségû, nagy érzékenységû filmek megjelenése óta a negatívnál sokkal nagyobb másolatok is készíthetõk. A pozitív képet a negatívhoz hasonlóan rögzítik és mossák. Azokat a vegyszereket, amelyek az "egyperces (instant) eljáráshoz" (a Polaroid típusú képek elõállításához) szükségesek, a film vagy a fényképezõgép már tartalmazza: az exponált filmrõl azonnal megszületik a papírmásolat. A diapozitívok készítésekor a "negatív lépést" kihagyják; a "fordítós" filmeket rendszerint színes diákhoz használják.

A színes fényképezéshez kétféle módszert dolgoztak ki. A ma már ritkán alkalmazott additív eljárás során a gépbe belépõ fényt fotográfiás úton kék, zöld és vörös komponenseire bontják, és a negatív kép segítségével olyan arányban keverik a kék, zöld és vörös fényt, hogy a fényképen a téma eredeti színei jelenjenek meg. A szubtraktív eljárás alkalmazásakor a pozitív rétegeken a kék, zöld és vörös fénnyel felvett negatív kép kiegészítõ színeiben (sárgában, bíborban és kékeszöldben) jelenik meg a kép. Az eredeti színeket az egymásra helyezett három pozitív réteg adja vissza. Tágabb értelemben a fényképezés olyan leképezést is jelent, amelyhez szemmel nem látható (ultraibolya vagy infravörös) sugarakat használnak, és a képeket kémiai vagy fizikai folyamatok révén a sugárzásra érzékeny anyagon rögzítik.

A meleg tárgyak infravörös sugarakat bocsátanak ki. Ha a tárgyakról infravörös-érzékeny filmre készítenek felvételt a sötétben, a képen megjelenik a felület hõmérséklet-eloszlása. A távoli tárgyakról is éles kép készíthetõ, mert az infravörös fény kevésbé szóródik a légkörben, mint a látható fény. Az eljárást gyakran alkalmazzák a csillagászok: a légköri pára miatt láthatatlan csillagok és csillagködök infravörös fényképeken jól tanulmányozhatók. Az infravörös fényképezést felhasználják a festett vagy más módon kezelt kelmék hibáinak kimutatására, a régi és megváltoztatott iratok kibetûzésére, olyan légi felvételek készítésére, amelyeknek alapján megállapítható a folyók és a tavak szennyezõdése, és kiválaszthatók az erdõk beteg fái. A katonák infravörös fényképezéssel különböztetik meg az álcázást a falevelektõl, mert a klorofill nem nyeri el az infravörös sugarakat.

Az ultraibolya fényképhez a tárgyat ultraibolya fénnyel világítják meg. A közvetlen eljárás alkalmazásakor a fotó a tárgyról visszavert ultraibolya fénnyel készül. A fluoreszcenciás módszer során az ultraibolya fény a tárgyban fluoreszcenciát kelt (látható fény keletkezik), és ennek a fluoreszcens fénynek köszönhetõ a fényképhez szükséges megvilágítás.
Az ultraibolya fényképezés festmények, kerámiák, papírfajták azonosítására, iratokon végrehajtott törlések kimutatására használható. Minthogy a légkörben a rövid hullámhosszú ultraibolya sugarak erõsen szóródnak, az ultraibolya fényképezés nem alkalmas tájképek megörökítésére: az ultraibolya fényképek elmosódottak, és nincsenek rajtuk árnyékok.
Az infravörös és ultraibolya fényképezéshez hasonló eljárás nyomán keletkeznek képek röntgensugarak, elektronsugarak és radioaktív sugárzás hatására (radiográfia). A fénnyel alkotott képek felvétele és elektromágneses jelekként való továbbítása (televíziózás és videózás) szintén a fényképezés egyik válfaja.

Összetett optikai eszközök

A vizuális optikai eszközöket akkor alkalmazzuk, ha valamilyen szabad szemmel nem jól látható tárgyat vagy annak részletét láthatóvá akarjuk tenni.

Az optikai eszközök lencséi a tárgyról a szemünkbe érkezõ fény látószögét nagyobbá teszik, így tehát a mikroszkóp esetén az eredeti tárgynál nagyobb képet kapunk, a távcsövek pedig a látószög növelése mellett a pontszerû tárgyak esetén a tárgyról eredetileg szemünkbe jutó fény mennyiségét is megnövelik. A vetítõk a tárgyról ernyõn felfogható, nagyított képet állítanak elõ.
Bár az eszközök alapelve és -szerkezete általában egyszerû, a leképezéskor fellépõ hibák kiküszöbölésére számos "segédeszközt": elõtétlencséket, nyalábhatároló rekeszeket (apertúra), akromatikus és más korrigáló lencséket is alkalmazni kell.

Távcsõ

A távcsövek felépítése  lényegében hasonló a mikroszkópok felépítéséhez, egy objektívbõl és egy okulárból állnak. Az objektív lehet gyûjtõlencse (pl. Kepler-távcsõ) vagy homorú tükör (pl. Newton-féle távcsõ), az okulár pedig gyûjtõ- vagy szórólencse (pl. Galilei-féle távcsõ) egyaránt.

A binokuláris (pl. színházi) távcsõben az objektív képét képfordító prizmák vezetik az okulárhoz (lencséhez), így a négyszeri visszaverõdés miatt a végsõ kép egyenes állású és a jobb- és baloldala sincs felcserélve. Mivel a távcsõ nagyítása függ a fénynek a két lencse közti útjától, a prizmákkal a távcsõ hossza jelentõsen csökkenthetõ.

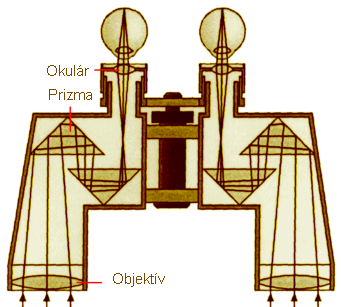
A csillagászati távcsövek egyik típusa a Cassegrain-féle távcsõ. Ebben egy középen átfúrt parabolikus tükörrõl egy segédtükörre esnek a sugarak, majd errõl visszaverõdve hozzák létre az okulárral szemlélhetõ képet.

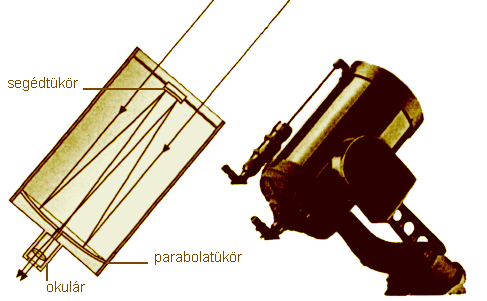
A vetítõk

A vetítõkészülékek egy megvilágított tárgyról gyûjtõlencse és a vetítõobjektív segítségével valódi, nagyított képet állítanak elõ egy ernyõn. Mivel a nagyításkor a kép fényerõssége jelentõsen csökken, a vetítõk erõs fényforrást használnak, leképezõ rendszerük tervezésekor pedig fontos szempont, hogy a tárgyat átvilágító összes fénysugár a rendszerben maradjon és részt vegyen a leképezésben is.

Az írásvetítõk esetén a fóliát átvilágító lencse a megvilágító felülettel azonos, igen nagyméretû Fresnel-lencse. Amint az az ábrán is látható, ennek sajátossága az, hogy a törõ felület koncentrikus körökre vágva egy síkba van tolva. Így a lencse átmérõje úgy növelhetõ, hogy vastagsága és súlya elhanyagolható marad.

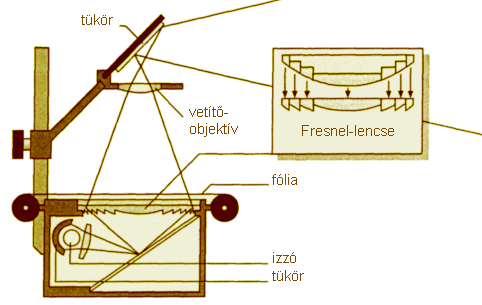
35. Fontosabb optikai eszközök és működésük II: mikroszkópok, távcsövek.

Távcső:

A távcső távoli tárgyak látószögének felnagyítására szolgáló eszköz. szokás még teleszkópnak vagy messzelátónak hívni.

Már az ókorban, Asszíriában is képesek voltak viszonylag jó minőségű lencséket készíteni, de az csak feltevés, hogy távcsövet is készítettek. Az optikai lencsét már ismerték az arabok és a perzsák is. Az első távcsövet Hans Lippershey készítette Hollandiában, 1608-ban. Ezután Galileo Galilei is megépítette a saját távcsövét, és csillagászati megfigyelésekhez használta. Felfedezte vele a Jupiter 4 holdját, és a holdi hegyeket. Johannes Kepler írta le elsőként az optikai lencsék tulajdonságait, és használatát.

A távcsöveknek két fajtája van: lencsés és tükrös (reflektor).

Lencsés távcsövek:

A lencsés távcsövek a fénytörés (más szóval refrakció) elvén működnek, ezért refraktoroknak is hívják őket.

Kepler-féle csillagászati távcső: A Kepler-féle csillagászati távcső két gyűjtőlencséből áll. A tárgylencse a távoli tárgyról valódi, fordított képet a gyújtópontja (K1) közelében. Ezt a képet a szemlencsével, mint egyszerű nagyítóval nézik. A két lencsét úgy állítják össze, hogy a távcső belsejében lévő gyújtó pontjuk körülbelül egybeessen. A távcső hossza (L) a két gyújtópont távolságának az összege lesz (L= f1+f2). A szögnagyítás a tárgylencse (f1) és a szemlencse (F2) gyújtótávolságának hányadosa lesz: N = f1/f2

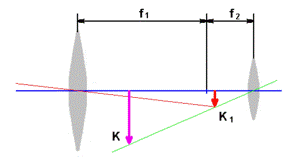
Galilei-féle (hollandi vagy földi) távcső:

A Galilei-féle távcsőben az objektív gyűjtőlencse, az okulár szórólencse. Egyenes állású, látszólagos képet ad. Az objektív sugármenetében, még mielőtt a gyűjtősíkjában a valódi kép létrejönne, a kis gyújtótávolságú szórólencse (okulár) a sugarakat széttartóvá teszi és így egyenes állású (K) kép keletkezik. A távcső hossza a két gyújtótávolság különbsége: L = f1-f2. A szögnagyítás a tárgylencse (f1) és a szemlencse (f2) gyújtótávolságának hányadosa: N = f1/f2.

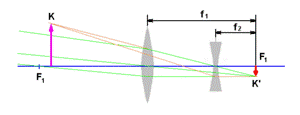
Tükrös távcsövek:

A tükrös távcsövek (reflektorok) esetében a fénysugaraknak egy görbült felületű (homorú) tükrön való visszaverődése révén jön létre a kép. A végtelen távoli tárgyról érkező párhuzamos fénysugarak a tükör felületén történő visszaverődés után annak gyújtópontjában fordított állású, valódi képpé egyesülnek. A legtöbbször üvegből készült tükör felületét alumíniumból, vagy más fémből álló vékony réteggel vonják be, amelyre gyakran egy kvarc védőréteg is kerül.

Mikroszkóp:

A mikroszkóp összetett nagyítórendszer, amely két gy jt lencse-rendszer segítségével

kisméret tárgyak jelent sen nagyított, fordított állású látszólagos képét állítja el

Történelmileg a csillagászati távcs b l alakult ki.

Minden mikroszkóp értéke els sorban a nagyításától és a felbontóképességét l függ. A

nagyítás mértéke a megfigyelt tárgy egyes részeinek lineáris növekedése, a

felbontóképesség pedig az a szög, amely alatt két különálló pontot még külön-pontként

érzékelünk. Az emberi szem felbontóképességének határa egy ívperc (1'). A látószög a

tárgynak szemünkhöz való közelítésével növelhet , ennek azonban határt szab az a tény,

hogy a tiszta látás távolságán (250 mm) belül szemünk már nem lát élesen. Ezért van

szükség olyan optikai eszközre, amely a látószöget növeli.

Bármilyen tökéletesen csiszolt lencse esetén is a fény hullámtermészete miatt a lencse

befogadónyílásán fényelhajlás lép fel, aminek következtében egy pontszer tárgy képe nem

pontszer lesz, helyette egy kis fényl korongot kapunk. Mivel ezek a kis korongok átfedik

egymást, megakadályozzák, hogy tetszés szerinti finomságú struktúrát észlelni tudjunk. Az

Abbe-törvény értelmében a felbontóképesség az alábbi képlettel számítható ki:

l

d=0,61×

n × sin a

d: felbontóképesség

l: a tárgyat megvilágító fény hullámhossza

n: a tárgy és a lencse közötti közeg törésmutatója

a: a tárgyról az objektív frontlencséjébe még éppen bejutó fénysugár és az optikai tengely

által bezárt szög (nyílásszög fele)

36. A fényinterferencia feltételei. A koherencia fogalma. A hullámfront osztáson alapuló (Young-Fresnel féle) interferenciajelenségek.

A koherencia

Mechanikai hullámok esetén közismert, hogy ha két hullám a hullámtér egy pontjában találkozik, az abban a pontban mérhetõ kitérés a két hullám adott pillanatban tapasztalható kitérésének eredõje lesz. Ha például csendes esõben egy vízfelületet figyelünk, azon apró, szabálytalanul változó fodrozódást látunk, amelyet a becsapódási helyekrõl kiinduló elemi hullámok "összege" ad. Ha két különbözõ pillanatban fényképet készítünk a vízrõl, a két kép egészen biztos, hogy különbözõ lesz. A vízfelületen azonban létrehozhatunk olyan hullámtalálkozást is, amelynek képe állandó marad. Ha például két, egymástól állandó távolságban lévõ pontban állandó frekvenciával, folytonosan ütögetjük a vízfelszínt, azon szabályos vonalak (hiperbolák) mentén minta rajzolódik ki.

A minta állandóságához három feltételnek kell teljesülnie: A két hullámforrás helyzete egymáshoz képest ne változzon A két hullámforrás frekvenciája legyen azonos A rezgés huzamosabb ideig tartson
Vízfelületen kialakuló interferenciakép

Ha két hullámra az elõbbi feltételek fennállnak, a két hullámot koherensnek nevezzük. Koherens hullámok találkozásakor állandó térbeli mintázat, azaz interferenciakép alakul ki.

Interferencia természetesen fényhullámok találkozásakor is kialakulhat, ha az elõbbi feltételeket biztosítani tudjuk. Ez azonban nem egyszerû feladat, hiszen a fény atomi gerjesztési folyamatok során, statisztikai véletlenszerûséggel jön létre, kibocsátását nem tudjuk kívülrõl befolyásolni. Ezért két különbözõ fényforrás fénye nem lehet koherens, két zseblámpával nem lehet interferenciát elõidézni. A megoldás az lehet, hogy ugyanazon fényforrás fényét osztjuk két részre, és különbözõ úton ugyanabba a pontba juttatjuk. (A két út hosszának különbsége nem lehet túl nagy, mert a fényhullám nem folytonos, hullámvonulatokból áll, és ezek túl nagy úthosszkülönbség esetén elkerülik egymást.)

37. Amplitúdó osztáson alapuló interferencia. Michelson interferométer.

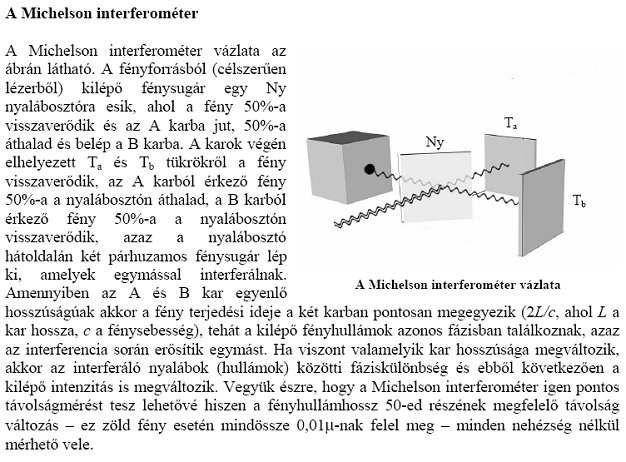
38. Interferencián alapuló optikai eszközök. Michelson, Sagnac interferométer működése és alkalmazása.

 

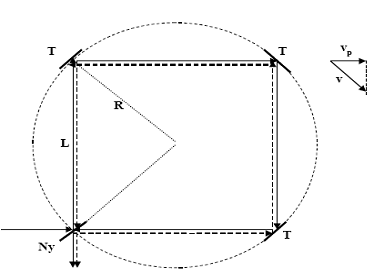
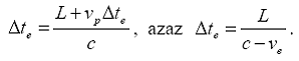
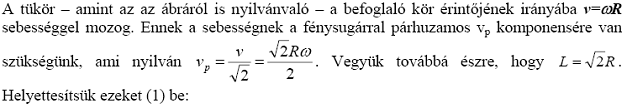
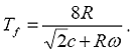
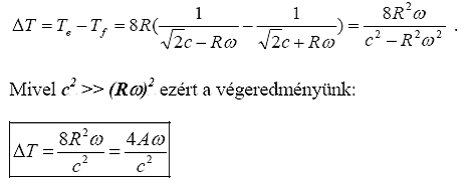
39. A fényelhajlás alapjelenségei. A Fraunhofer-féle elhajlás. Fraunhofer-féle elhajlás résen, kör alakú nyíláson.

1.Fraunhofer elhajlás (diffrakció) résen

A rés minden pontjából másodlagos hullámok indulnak ki az a irányba, és ezek interferálnak. Az eredő hullámot a komplex amplitúdók összegezésével kapjuk meg. Mivel a résben végtelensok pontból indulnak a másodlagos hullámok, integrálunk az y irány mentén a rés teljes szélességén. Így az a irányban észlelt eredő komplex amplitúdó

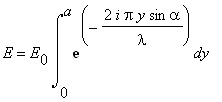
Felhasználjuk az Euler-féle formulát, nevezetesen az e^ix=cos x +i sin x azonosságot, a továbbá azt, hogy az intenzitás= E.E_konjugált a következő összefüggést kapjuk:

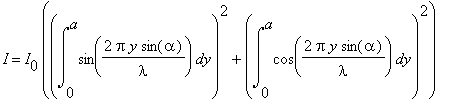
Ezután kiszámítva az integrálokat:

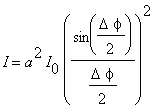
ahol a Df a fenti jelentéssel bír. Namost: az a szög lévén kicsi, amennyiben csak 2-3° értékű vagy ennél kisebb, sin a = tg a jó közelítéssel, ezért sin a= u/F(lásd az ábrát). Ez az összefüggés a fény intenzitáseloszlását adja meg, a maximális intenzitást egységnyinek véve, a vízszintes tengelyen a fokális síkban felfele mutató u tengelyt adtuk itt meg. Ez kb így néz ki:

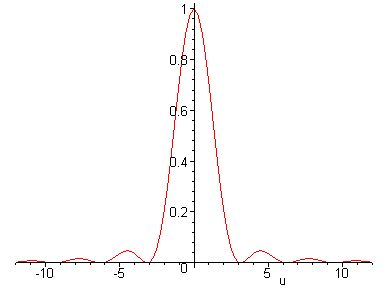
Ugyanez, szemből nézve (monokromatikus fényre, nem pedig fehér fényre!):

Fehér fény esetén az oldalsó maximumok kicsit a hullámhossztól függően más-más helyen keletkeznek, ezért az oldalsó maximumok színesek. Megemlítem, hogy az itt látható ábrát egy kissé "túlexponáltam", mert az elsőrendű maximum a középsőnek csupán 4,72 %-a, a másodrendű pedig csupán 1,65 %-a, a többi csak erős fényben látszik. Érdekes módon az emberi szem ezeket is érzékeli, ami sokat elárul a szemünk érzékenységéről.

40. Az optikai leképezés hullámelméletéről. Az optikai eszközök feloldóképessége. A fotolitográfia optikai problémái.

Meddig lehet fokozni a mikroszkóp nagyítását?
Azt gondolhatnánk, hogy a végtelenségig. Mert látszólag nincs akadálya annak, hogy például az 1000-szeresre nagyított képet újra 1000-szeresen tovább nagyítsuk, és akkor 1000 ^. 1000 = 1 milliószoros vagy még nagyobb nagyítást érjünk el.
Ez azonban nincs így. A mikroszkóp nagyításának határa van. A fénnyel dolgozó mikroszkópot legfeljebb 2000-szeres nagyításig alkalmazzák. Miért nem készítenek még jobban nagyító fénymikroszkópot?

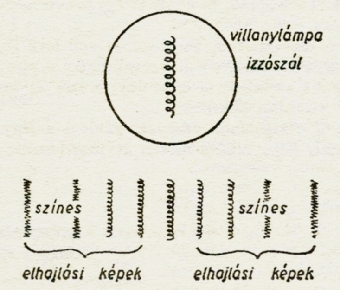Ennek okát azonnal megértjük egy kísérlet alapján, amelyet bárki odahaza elvégezhet. Nyissuk ki esernyőnket ás az ernyő szövetén át nézzünk körülbelül 2 méter távolságból egy villanylámpa izzószála felé. Meglepő látványban lesz részünk: egy izzószál helyett 7 - 8 izzószál-kép jelenik meg egymás mellett (úgynevezett elhajlási képek), a szélsők pedig feltűnően szivárványszínűek lesznek. (ábra)

Nézzünk a kinyitott esernyő finom és sűrű szövésű szövetén át a villanylámpa egyenes izzószála felé. Egyetlen izzószál helyett sok izzószálat látunk. A széleken látható izzószálak szivárványos színeződése feltűnő

A mikroszkópon át vizsgált tárgyon is vannak átlátszatlan ás átlátszó
helyek sűrűn egymás mellett - éppen úgy, mint az esernyő szövetén.
Ezért egymáshoz igen közeli nyílásokon, réseken át halad a fény. De tudjuk, hogy ilyenkor szivárványszínekkel szegélyezett kép keletkezik, ami a körvonalakat elmosódottá teszi. Tehát az egymáshoz közeli részletek a tárgyon nem ismerhetők fel.
De még egy más körülmény is határt szab a közeli részletek felismerhetőségének. Mennél szűkebbek a részletek közötti rések, annál jobban elhajlanak egymástól az elhajlási képek, amiket kísérletünkben megfigyelhettünk. Végül egyetlen elhajlási kép sem jut a mikroszkóp tárgylencséjébe. A tapasztalat szerint ilyenkor nem ismerhető már fel két pont különállósága a vizsgált tárgyon. Ilyen okok miatt a leggondosabban javított lencsékkel sem érdemes a tárgyat 2000-szeresnél jobban megnagyítani.
Érdemes megjegyezni a következőket:
Szabad szemmel két egymás mellett levő pontot még külön látunk, ha a két pont távolsága nem kisebb, mint 0,1 mm. Ezt úgy mondjuk, hogy szemünk felbontóképessége 0,1 mm, a tiszta látás távolságából (25 cm). Ha kisebb a két pont közötti távolság, a pontok képe összefolyik szemünkben,
Fénymikroszkóppal (a legjobbal) szemünk még különválaszt két pontot
egymástól, ha a közöttük levő távolság 200-szor kisebb, mint az előbbi
0,1 mm. Tehát a legkitűnőbb fénymikroszkóp feloldóképessége 0,1 mm : 200
= 0,0005 mm. Ez akkora távolság, mint a fény közepes hullámhossza.

fotolitográfia - A mikroelektronikai eszközök gyártásánál használt el­járás, amelynek során a félvezető felületre felvitt speciális rétegen maszkot alakítanak ki a létrehozni kívánt szerkezetnek megfelelően. A speci­ális fény­érzékeny réteg a megvilágítás hatására eltávolíthatóvá válik; ahol nem érte fény, ott viszont megmarad. Az így kialakított maszk bizonyos részeket el­szigetel, másokat elérhetővé tesz például szennyezők bevitele, maratás, vagy más technológiai eljárások számára, amelyekkel a mikroelektronikai eszköz különböző szerkezeteit kialakítják. A gyártás során számos ilyen, néhány tized mikron vastag réteg kerül egymás fölé. A korábbi, kisebb integráltsági fokú eszközöknél a megvilágításra egyszerű fénysugarakat használtak, mivel azonban a fénysugár mérete határt szab a kialakítható szerkezet méretének, a nano-méretekhez közelítve újabban a megvilágítást speciális optikai eszkö­zökkel, lézerrel, röntgen- illetve gammasugarakkal valamint elektron- és ionsugarakkal végzik, a minél kisebb méretek elérése érdekében. Az ezzel a módszerrel elméletileg elérhető legkisebb méret 35 nm körül van, melyet a becslések szerint (International Semiconductor Roadmap) 2014-re érnek el. Ez alatt a méret alatt technológiaváltásra lesz szükség, az új technológia várhatóan a molekuláris nanotechnológia lesz.

A felbontóképesség

Az optikai leképezõ rendszereknek egyik legfõbb jellemzõje az úgynevezett felbontóképesség. A leképezéskor alapvetõ elvárás, hogy a tárgy két különbözõ pontjáról a képen is két különálló képpont keletkezzen. Elvileg ez csupán a nagyítás mértékén múlik, gyakorlatilag azonban fizikai korlátai vannak. A képpontok ugyanis sohasem matematikai értelemben vett kiterjedés nélküli pontok, mert a megvilágító nyaláb határán illetve a nyalábot határoló foglalatokon a legtökéletesebb leképezés esetén is elhajlik a fény. Kör alakú foglalat alkalmazásakor az elhajlás miatt a pont képe kis korong lesz.

Amint azt már a résen való elhajlás esetén láttuk, az elhajlás mértéke (és így a korong átmérõje) egyenesen arányos a fény hullámhosszával és fordítottan arányos a leképezõ nyaláb átmérõjével (vagyis a rés méretével). Két pont képe, vagyis két ilyen elhajlási korong akkor látszik különbözõnek, ha az egyik elhajlásképének erõsítési helye a másik elhajlásképének kioltási helyére esik. Ezt a (szöggel jellemzett) távolságot felbontási határnak, ennek reciprokát pedig felbontóképességnek nevezzük.

41. Polarizáció. Dikroizmus, kettőstörés. Optikai aktivitás. Polarizátorok, a fény polarizációján alapuló eszközök.

A hexagonális rendszer romboéderes osztályába sorolt kalcium-karbonát kristály (CaCO₃), vagy a kvarckristály - amelynek szemben lévő oldalai mindig párhuzamosak - meglepetéssel szolgálhat. A speciális plánparalel lemezen keresztül "szellemképesnek" látjuk a világot. A megtört sugárból kettő figyelhető meg, ezek közül az egyik "engedelmeskedik" a Snellius-Descartes-törvénynek, ez a rendes, vagy ordinárius sugár. A másik a rendellenes, vagy másképpen extraordinárius sugár nem tesz eleget a törési törvénynek. A jelenség oka, hogy a kristályon belül különböző irányokban más a törésmutató, ez a magyarázata a másik sugár létrejöttének. A kristályon kilépő két sugár síkban poláros és a két polarizációs sík merőleges egymásra. Ezt a jelenséget hívjuk kettőstörésnek.

Egy másik ásvány, a turmalin is képes polarizált fényt előállítani. Itt a poláros fény keletkezésének mechanizmusa más. Ez a kristály a fény két egymásra merőleges polarizáltságú komponensét eltérő módon nyeli el, abszorbeálja. Ez a dikroizmus jelensége. E tulajdonság számos ásványra és néhány szerves vegyületre is jellemző. Herapathnak 1852-ben sikerült előállítani kinin jódszulfátból ilyen kristályt mesterségesen. 1932-ben találta fel Land a Polaroidot, amelyet számos helyen alkalmaznak azóta is.

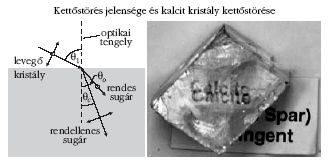
42. A holográfia alapjai.

3.6.1. A holográfia elve

A lézerek alkalmazásának egyik legizgalmasabb, leglátványosabb területe a holográfia. A pénzek hologramcsíkjaitól és más holografikus védjegyektõl a mûvészi hologramkiállításokon át a tudományos alkalmazásokig sok helyen találkozhatunk vele. Az emberek többségének nagy élményt jelent, hogy a fény valami megfoghatatlan test térbeli képét rajzolja a szemük elé.

Mi a különbség a hologram és a fénykép között?

A holográfia olyan képrögzítõ eljárás, amellyel a tárgyról tökéletes térhatású, vagyis háromdimenziós kép hozható létre. A hagyományos fényképezés során a tárgy képét lencserendszerrel képezzük le a film síkjára, és így a filmen a tárgyról kiinduló fény intenzitásának megfelelõen az egyes pontokban feketedés jön létre. Ennek az eljárásnak a során azonban - mivel a feketedés mértéke csak a fény erõsségétõl (vagyis amplitúdójától) függ, és független a fényhullám másik jellemzõjétõl, a fázistól -, minden információ, amit a fázis hordoz (s ami a hullám rezgésállapotára jellemzõ), elvész. A tárgynak minden egyes pontja ugyanabba a síkba képzõdik le, a kép kétdimenziós lesz. A holográfia lényege éppen ennek a hiányosságnak a kiküszöbölése: a hologramon - voltaképpen egy sík lemezen - az intenzitás mellett a hullám fázisát is sikerül rögzíteni, így lehetségessé válik a teljes információ felvétele és tárolása. (Innen ered a holográfia elnevezés is: görögül a "holosz" teljest, a "grapho" pedig írást jelent.)

Az eljárás ötletét Gábor Dénes magyar származású tudós vetette fel és dolgozta ki 1947-ben. Bár az elmélet jó volt, az elsõ hologram elkészítésére csak 1961-ben kerülhetett sor, mert addig - a lézer megjelenéséig - nem állt rendelkezésre olyan fényforrás, amely az interferencia elõállításához szükséges koherenciát biztosítani tudta volna. Gábor Dénes munkáját 1971-ben Nobel-díjjal ismerték el.

Ha megvilágítunk egy tárgyat, akkor a Huygens-elv szerint annak minden egyes pontja másodlagos hullámforrássá válik, elemi gömbhullámok indulnak ki belõle. A tárgytól elég kis távolságban ugyanabban az idõpillanatban az egyes elemi hullámok hullámfrontjai az õket létrehozó másodlagos forrásoktól azonos távolságra helyezkednek el, vagyis az összes elemi hullámot beburkoló eredõ hullámfront a tárgy alakjáról hordoz információt, ahhoz hasonló.

Ha a tárgy felületén kisebb egyenetlenségek vannak, akkor a tárgytól nagyobb távolságban - egyszerû geometriai okok miatt - a hullámfront valamelyest kisimul és kisebb szeletei már síkhullámnak tekinthetõk.
Ez a változás azonban csak a burkoló hullámfront alakját érinti, nem jelent információveszteséget, a hullámfront továbbra is arra és csakis arra a tárgyra lesz jellemzõ, amelyrõl a fény kiindult. Ez a hullám tulajdonképpen a forrásától függetlenül halad tovább.
Ha valamilyen ok miatt már nincs "mögötte" a tárgy, de a hullám a szemünkbe jut, ott a kép akkor is létrejön, látjuk a tárgyat. (Persze a fénysebesség nagysága miatt csak igen szoros idõtartamon belül.) A holográfia lényege éppen ebben rejlik. Ha egy eljárással sikerül a tárgyról kiinduló hullámot egy adott helyen rögzíteni, és késõbb "újraéleszteni", a hullám ugyanúgy halad tovább, mint azelõtt, és ugyanolyan érzetet is kelt.

3.6.2. Hogyan készíthetünk hologramot?

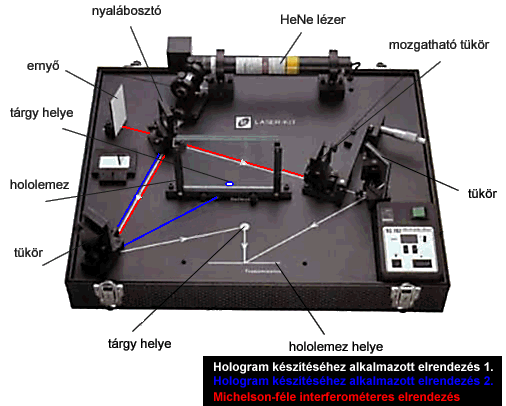
A felvétel lényege tehát a tárgyról kiinduló hullámfront rögzítése. Ez úgy történik, hogy a tárgyhullám és egy vele koherens másik síkhullám, az úgynevezett referenciahullám segítségével interferenciaképet hozunk létre, ezt a képet pedig egy fényképlemezen vagy filmen rögzítjük.

A lemezen elõhívás után - a tárgy struktúrájának bonyolultságától függõen - egyszerûbb vagy összetettebb vonalrendszer látható, ez maga a hologram. Ezen sem a tárgy alakját, sem egyéb jellemzõit nem lehet felfedezni.
A reprodukálás a következõ módon történik: abból az irányból, ahonnan felvételkor a referenciasugár a lemezre esett, fényt bocsátunk a hologramra. A megvilágító fényforrás hullámfrontja a hologramon való áthaladáskor "szétroncsolódik". A rögzített interferenciastruktúrán a hullám (a fázisugrástól eltekintve) ugyanúgy halad tovább, mint a felvétel során, hiszen a világos és fekete csíkok megfelelnek a kioltási és erõsítési helyeknek.
Így éppen az a hullámfront fog kialakulni, amely a tárgyról kiindult és amelyet a hologramon konzerváltunk.
Ha a megfelelõ irányból nézzük a képet, az az érzetünk alakul ki, mintha a tárgy a maga háromdimenziós valójában állna elõttünk.

A hologram felvételének és rekonstruálásának lényege tehát: megfelelõ módon rögzítjük, illetve a rögzített interferenciakép segítségével újra létrehozzuk "továbbengedjük" azt a hullámfrontot, amely a tárgyról kiindult. Ennek alapján könnyen magyarázhatók a hologramkép sajátos és szokatlan tulajdonságai.

Mivel a valódi tárgyról kiinduló és a rekonstruált hullám megegyezik, azt ugyanúgy is látjuk. A látott kép háromdimenziós, érzékelhetõ a térbeli mélység, és lehetõvé válik az oldal- és függõleges irányú rálátás is, a kép "körbejárható". A hologramon a tárgy képe végtelen sok perspektívából van rögzítve, s ha a megfigyelõ mozog, más és más perspektívát érzékel, amelyek folyamatosan mennek át egymásba, így az elrendezéstõl függõen lehetséges, hogy az egyik irányból takart vagy nem látható részlet valamelyik másik irányból nézve láthatóvá válik.
A hologramok mélységélessége igen nagy - csupán a fényforrás koherenciahossza szab határt neki -, ezért ha a tárgy egyes részeinek mélysége eltérõ, akkor a róluk kapott kép szemlélésekor is változtatni kell a szem fókusztávolságát.

Mivel a hologram felvételekor nem használunk objektívet, nem történik a képnek a hagyományos értelemben vett leképezése, a tárgy minden egyes pontjából a hologram bármely pontjába érkezik információ. Emiatt nincsenek olyan pontok, elemek a hologramon, amelyek emlékeztetnének az eredeti tárgy jellegzetes vonalaira, és ez az oka annak a meglepõ tulajdonságnak, hogy a kettétört hologram is elõállítja a tárgy teljes képét.
Ha ugyanis a hologram valamilyen módon megsérül (karcolás, folt, törés), csupán azok a perspektívák tûnnek el a képbõl, amelyeket a sérülés érintett, a többi megmarad.
Természetesen ez is információ- és intenzitásveszteséggel jár, és ha a hologramnak csak kis darabjával állítjuk elõ a képet, a felbontóképesség is csökken.

3.6.3. A hologram alkalmazásai

A hologramok legelterjedtebb alkalmazási formájával, a biztonsági azonosító jelekkel mindenki találkozhatott a kazettákon és CD-ken vagy az új papírpénzeken, bankkártyákon. Ezek az apró kis hologramok (szinte) hamisíthatatlanok, mert róluk tökéletes másolatot csak az eredeti hologram segítségével lehet készíteni.
Az apróbb-nagyobb dísztárgyként, mûvészeti alkotásokként forgalmazott hologramokon túl ma már tökéletesen hû, nagyméretû színes hologramokat, sõt színes holofilmeket is készítenek. A hologramok felhasználási területe azonban - az információtárolás sajátságai miatt - jóval szélesebb, és a szoros értelemben vett háromdimenziós képrögzítésnél sokkal több lehetõséget nyújt. Példaként ezek közül a lehetõségek közül ragadjunk ki néhányat:

A tárolt térbeli információ speciális felhasználásai

Több hologram szuperpozíciója ugyanazon a lemezen

Az információ optikai feldolgozása

3.6.4. Holográfia az atomok világában

A Magyar Tudományos Akadémia Szilárdtestfizikai és Optikai Kutatóintézetének két munkatársa, Tegze Miklós és Faigel Gyula érdekes módszert dolgozott ki az anyag belsõ szerkezetét feltáró, úgynevezett atomi hologramok elõállítására.

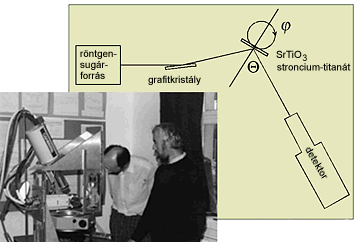
A képet alkotó sugárzás forrásaként magának a vizsgálni kívánt anyagnak az atomjait használták, amelyek külsõ, gerjesztõ röntgensugárzás hatására elektronokat vagy röntgenfotonokat bocsátanak ki.

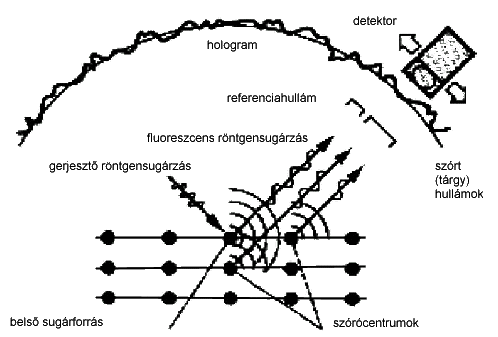
Az ilyen sugárzás egy része kölcsönhatás nélkül lép ki az anyagból (ez lesz a referencianyaláb), miközben a sugárzás másik része szóródik a környezõ atomokról. A kettõ interferenciája adja a hologramot, amely a sugárzó atom környezetére vonatkozó összes információt tartalmazza. A képalkotáshoz egyetlen atom sugárzása nem elég, sok sugárzó atom azonban már elegendõ fényt adhat. Ezért atomi hologramok készítésével a kristályos anyagok esetében érdemes próbálkozni.

Ha a technikai problémákat sikerül megoldani, az atomi felbontású röntgenholográfia a tudomány számos területén alkalmazható. Kiegészítheti a hagyományos diffrakciós kísérleteket az atomok helyének a meghatározásában. Néhány területen olyan információkat is szolgáltathat, amelyek más módszerekkel nehezen elérhetõk. Például megmutathatja, hogy a mikroelektronikában használatos félvezetõk adalékatomjai körül hogyan helyezkedik el a többi atom. A fejlõdés egy másik lehetséges útja az, hogy az atommagok gamma-sugárzásának felhasználásával készítenek hologramot. Az atommagok bizonyos - nagyon szûk - energiatartományban gamma-sugarakat bocsáthatnak ki, illetõleg azokat erõsen szórják. Ez a szórás akár egy nagyságrenddel is nagyobb lehet, mint a szokásos - az atom elektronjain végbemenõ - szórás. Az erõsebb kölcsönhatás a hologramban is sokkal nagyobb változásokat idéz elõ, s ez megkönnyíti a mérést. E szórás másik nagy elõnye, hogy érzékeny a kristály belsejében található mágneses térre, így láthatóvá tehetõ a kristály mágneses szerkezete is.

Az atomi felbontású röntgenholográfia jelenleg még a fejlesztés és a kipróbálás szakaszában van. Az eredmények biztatók, és azt mutatják, hogy a módszer - technikájának további finomításával - hozzájárulhat a mikrovilág, az atomi és molekuláris szerkezet mélyrehatóbb megismeréséhez. Ez pedig lehetõvé teszi, hogy jobb szerkezeti anyagokat, hatásosabb gyógyszereket, biztonságosabb autókat és kevésbé környezetszennyezõ technológiákat dolgozzanak ki.