Vizsga matek

Vizsga matek

Tétel/definíció:

monoton sorozatok konvergenciájára vonatkozó 1 tétel kimondása

torlódási pont definíciója

zárt intervallumon folytonos függvényekre vonatkozó Bolzano tétel és Weierstrass tétel

pontbeli differenciálhányados

Feladatok:

1, Határozza meg a következö határértékeket:

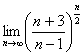
Az elsö két tényezöre bontható: (1/2)^n*n^2 és cosn. Azt nem vitatja senki, hogy az elsö tényezö 0-hoz tart. A cosn pedig egy korlátos sorozat (mindig 1 és -1 közötti). Na most van egy olyan tétel, hogy egy nullához tart sorozat és egy korlátos sorozat szorzata is nullához tart.

A második (1+1/n)^n alakra hozható, mégpedig úgy, hogy a zárójelen belül 1+4/(n-1) lesz. Itt n-1 az "x", így kitevöben is n-1nek kellene lennie. De nem az van, ezért itt is alakítani kell:

(1+4/(n-1))^(n-1), de hogy ugyan az maradjon, ezt még n/2-re is kell emelni az egészet, meg (n-1)-edik gyököt is kell vonni belöle, vagyis ezt együtt: n/(2n-2)-dik hatványra kell emelni.

[ (1+4/(n-1))^(n-1) ]^(n/(2n-2)) Itt a szögletes zárójelen belüli rész e^4-hez tart, a kitevöje meg ˝-hez, így az egész e^2-hez fog tartani.

2, Oldjuk meg az alábbi egyenletet a komplex számok halmazán, majd ábrázolja a gyököket a komplex síkon:

z^3=2i-2 egyenletet kell megoldani, vagyis a 2i-2nek kellenek a 3. gyökei. Ilyenböl ugye 3 darab lesz. 3. gyököt trigonometrikus alakból egyszerü vonni, ezért át kellene írni trigonometrikus alakba. Így fejböl ez gyök(8)*(cos(3pi/4)+i*sin(3pi/4)), de lehet hogy elcsesztem valahol. Szóval itt már csak alkalmazni kell azt a szabályt, ami a képletgyüjteményben is biztos benne van, és megkapjuk a gyököket és már csak be kell rajzolgatni a gauss számsíkra (ami kibaszás, mert egy csomó idö elmegy vele)

3/a, Legyen f függvény értelmezési tartománya [1,2], értékkészlete [3,5[. Határozza meg a függvény értelmezési tartományát és értékkészletét!

Ez sztem rohadtul nem egyértelmü, majd megkérdezem a Szirmait

/b, Ábrázolja a  függvényt! Tüntesse fel az értelmezési tartományt, értékkészletet és néhány jellemzö pontot!

Ilyesmi volt a 2. zh-ban is az egyik csoportnak, jó nagy hülyeség, mert viszi a drága idöt, meg figyelni kell, de egyébként nem nezéh.

4/a, Folytonossá tehetö-e a sign függvény? Indokoljon!

Természetesen nem tehetö folytonossá, a 0 pontban van szakadása, itt a bal- és a jobb oldali határértékek nem egyeznek meg (-1 és 1), ezért akármit csinálunk ez bizony nem lesz folytonos soha.

x² ha x≥1

/b g(x)   Igazolja, hogy g(x) folytonos, de x₀=1 pontban nem diffható!

x ha x<1

5, Adja meg az függvény inflexiós pontjait!

Ott van inf. Pont, ahol a 2. derivált 0 és elöjelet vált. Ha jól számoltam, ez +vagy- (gyök2)/2.

A másoik deriváltra amúgy most hirtelen -2*e^(-x^2)+(4x^2)*e^(-x^2) jött ki.

6/a

ez szopatós, vagy én nem jöttem rá az egyszerü megoldásra, de ez az eredmény:

tan(x)-x-1/3(cos(x))^3

/b Határozza meg az  függvény alatti területet!

I Vizsga

A1 Matematika

Elméleti kérdések: (Minden kérdés 3 pontot ér)

1. Valós számsorozat határértéke (minden típusát ismerni kell).
2. Egyváltozós valós-valós fgv. differenciálszámítása.
3. Bernoulli-egyenlötlenség
4. Lokális szélsöérték létezésének elégséges feltétele.

Példamegoldás:

5. Határozza meg az alábbi függvény határértékeket!

6. Oldjuk meg a komplex számok halmazán az alábbi egyenletet:

7. Egy terménytároló csúcsával lefelé fordított forgáskúpból és egy rajta nyugvó hengerböl áll. A kúp alkotója 3m, a hengeré 2m. Hogyan kell elkészíteni a maximális térfogatú tárolót? (8p)
8. Határozzuk meg az alábbi függvény inflexiós pontját:

9. Forgassuk meg az y=sin x  görbe [0,p] szakasz feletti ívét az x tengely körül. Számítsuk ki a keletkezett forgástest térfogatát. (6p)
10. Határozzuk meg az alábbi integrálokat: