Különbözõ áramköri szakaszokra vonatkozó Ohm-törvények

Az elektrosztatikus térnél tárgyaltakhoz hasonlóan, a stacionárius elektromos áram esetében is definiálhatjuk az elektromos potenciált és az elektromos feszültséget. Mivel a stacionárius elektromos áram elektromos tere ugyanúgy örvénymentes, mint az elektrosztatikus tér az általánosítás azonnali, tulajdonképpen átvesszük az ottani definíciókat. Az áramkör minden pontját jellemezhetjük az elektromos potenciállal, amelyet viszont minden esetben egy adott vonatkoztatási szinthez viszonyítva 515d37f kel megadjunk. Ez lesz a pont abszolút potenciálja. Ez a szint a legtöbb esetben a földpotenciál, amelyet nullának tekintünk. Azonban bármely más potenciálját is tekinthetjük vonatkoztatási szintnek, amely sokszor elõ is fordul kísérleti és ipari berendezések esetében. Két pont közötti potenciálkülönbséget feszültségnek nevezzük. A feszültség elõjeles skaláris mennyiség. Pozitívnak tekintjük azt a feszültséget, amelyet a magasabb potenciálú (pozitívabb) ponttól az alacsonyabb potenciálú (negatívabb) pont fele mérjük. Ez egy ellenállást nézve megfelel a technikai áramirányának, tehát a pozitív töltéshordozó irányának. Így megállapíthatjuk, hogy egy homogén anyagból készült ellenállás mentén az áramiránynak megfelelõen csökken az elektromos potenciál. Példaként tekinthetjük a 3.7 ábrán látható kapocsfeszültséget, amely a feltüntetettnek megfelelõen egy pozitív feszültség.

1. Ohm-törvénye generátor üzemmódú feszültségforrásra

Az alábbiakban tekintünk egy elektromotoros feszültségû és  belsõ ellenállású feszültségforrást, amelyet sematikusan a 3.13.a ábrán, áramköri helyettesítõ képét pedig a 3.13.b ábrán láthatjuk. A feszültségforrások abban az esetben vannak generátor üzemmódban amikor az áramköri ágban az áram iránya megegyezik az e.m.f. (vagyis az idegen térerõsség) irányával.

Célunk meghatározni az A és B pont közötti potenciálkülönbséget (feszültséget). Ehhez felhasználjuk az áramkör bármely részére érvényes differenciális Ohm-törvényt (3.33), melynek képezzük görbe vonalú integrálját a B ponttól az A pontig az alábbiaknak a  integrálási iránynak megfelelõen.

Elvégezzük a számításokat az alábbiaknak megfelelõen:

(ahol V_A és V_B a A és B pontok potenciáljai),

a feszültségforrás elektromotoros feszültsége.

Behelyettesítve a (3.2) összefüggésbe kapjuk az A és a B pont közötti potenciál-különbségére:

A 3.14 ábra a potenciál változását ábrázolja az A és B pontok között:

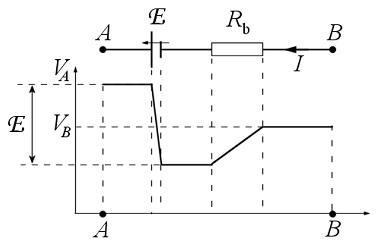
3.14 ábra

Hasonló számítást végezhetünk el arra az esetre is, amikor a feszültségforrás mellet az áramköri szakasz tartalmaz egy ohmos fogyasztót is. Az A és B pont közötti potenciálkülönbséget a (3.43) összefüggés adja meg. A 3.15 ábra tartalmazza az áramköri kapcsolást és a potenciál menetét.

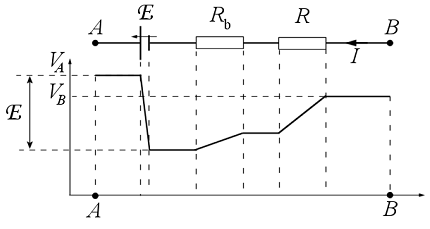
3.15 ábra

2. Ohm-törvénye fogyasztói üzemmódú feszültségforrásra

Az alábbiakban tekintünk egy  elektromotoros feszültségû és belsõ ellenállású feszültségforrást, amelyet sematikusan a 3.16.a ábrán, áramköri helyettesítõ képét pedig a 3.16.b ábrán láthatjuk. A feszültségforrások abban az esetben vannak fogyasztói üzemmódban amikor az áramköri ágban az áram iránya ellentétes az e.m.f. irányával.

Célunk meghatározni az M és N pont közötti potenciálkülönbséget (feszültséget). Ehhez újból az áramkör bármely részére érvényes differenciális Ohm-törvényt használjuk fel (3.33), melyet integrálunk az M ponttól az N pontig az alábbiaknak a  integrálási iránynak megfelelõen.

Elvégezzük a számításokat az alábbiaknak megfelelõen:

a feszültségforrás elektromotoros feszültsége.

Behelyettesítve a (3.44) összefüggésbe kapjuk az M és az N pont közötti potenciál-különbségére:

A 3.17 ábra a potenciál változását ábrázolja az M és N pontok között:

3.17 ábra

Hasonló számítást végezhetünk el arra az esetre is, amikor a feszültségforrás mellet az áramköri szakasz tartalmaz egy ohmos fogyasztót is. Az M és N pont közötti potenciálkülönbséget a (3.46) összefüggés adja meg. A 3.18 ábra tartalmazza az áramköri kapcsolást és a potenciál menetét.

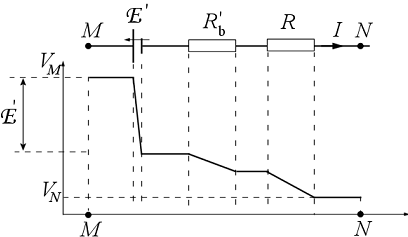
3.18 ábra