A Maxwell-egyenletrendszer

1.1. A vákuumra vonatkozó Maxwell-egyenletrendszer

A Maxwell-egyenletrendszer az elsö próbálkozás arra vonatkozóan, hogy a fizika különbözö területein megszerzett tudásanyagot egységesítse. A következökben tárgyalásra kerülö egyenletrendszer egységese tárgyalja az elektromosságtan, mágnességtan és optika jelenségeit. Már most megjegyezzük, hogy az (1.1-1.4) egyenletrendszer csakis vákuumra vonatkozik, mely nyugalomban van. A különbözö anyagi közegek hatását illetve mozgó közegeket a késöbbiekben tárgyalunk.

a)      I. Maxwell-egyenlet (Ampère-törvény) - zárt és nyitott áramkörök - eltolási áramsürüség

b)      II. Maxwell-egyenlet (Faraday-indukciótörvény)

c)      III. Maxwell-egyenlet - az elektromos tér forrásbösége

d)      IV. Maxwell-egyenlet - a mágneses tér forrásbösége

A Maxwell-egyenletrendszert a mai fizika elfogadja axiómaként, nem bizonyítja. A továbbiakban azonban mégis megvizsgálunk néhány fontos mozzanatot az egyletrendszer felírásához vezetö útból azért, hogy jobb rálátásunk legyen az egyenletek jelentésére és jelentöségére.

1.1.1. Az I. Maxwell-egyenlet

Az I. Maxwell-egyenlet kimondja, hogy a különbözö típusú áramsürüségek hozzájárulnak az örvényes mágneses tér kialakításához.

Történelmileg nézve ennek az egyenletnek az alakulását elöször meg kell vizsgálnunk, hogy miként számíthatjuk ki egy vezetö körül létrejövö mágneses tér indukcióját (vagy térerösségét). Ehhez két törvényt lehet felhasználni, az egyik a Biot-Savart-, a másik pedig az Ampère-törvény. Vizsgáljuk meg e törvények alakját zárt áramkörre vonatkozóan.

a.) A Biot-Savart-törvény

Ismert geometriai alakú vezetöben folyó áram által a tér különbözö pontjaiban létrehozott mágnes tér indukcióját (illetve térerösséget) az 1.1 ábra jelöléseivel a következö vonalintegrálok segítségével lehet kiszámítani: 535g66f

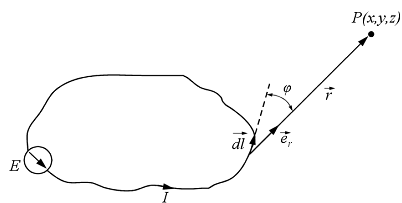
1.1 ábra

b.) Ampère (gerjesztési) törvény

A törvény kimondja, hogy egy vezetörendszer térében felvett bármely zárt görbe mentén a mágneses térerösség vonalintegrálja megegyezik az áramsürüségnek zárt görbe által kifeszített felületen számított teljes fluxusával (1.2 ábra), melyet a következö integrálegyenlettel fejezhetünk ki:

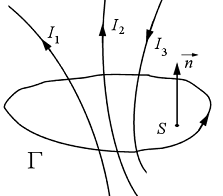
1.2 ábra

Mindkét integrálban találhatók olyan mennyiségek, amelyeknek irányítást kell adnunk, ilyenek a és mennyiségek. Ezek irányításait egymáshoz megfelelöen kell hangoljuk ahhoz, hogy a törvény érvényes legyen és számításaink ne legyenek hibásak. Elöször megválasztjuk a görbe körüljárási irányát, majd az felület felületelemeinek irányítását úgy választjuk meg, hogy a felületi meröleges a felület (domború) konvex oldalán található térrészben legyen. Ha a felület sík, akkor a felületi meröleges irányítása meg kell egyezzen a jobbsodrású fúró haladási irányával, melyet a Γ görbe körüljárási irányába forgatunk. Az összefüggés érvényes minden a görbe által kifeszített felületre. Az (1.6) összefüggés a gerjesztési egyenlet differenciális alakja. Felhasználva a Stokes-integrálegyenletet továbbalakíthatjuk az összefüggést és meghatározhatjuk a gerjesztési törvény differenciális alakját (1.7).

Megjegezzük, hogy a zárt áramkör elektromos szempontból azt is jelenti, hogy az elektromos áramsürüség vektorterének erövonalai zártak, vagyis az áramsürüség forrásmentes ().

Vizsgáljuk meg figyelmesen a fenti két törvényt. Arra a következtetésre jutunk, hogy az összefüggés ténylegesen kielégítö eredményre vezet a zárt áramkörök esetében, viszont ellentmondásokba ütközünk abban az esetben, amikor az áramkör tartalmaz olyan áramköri elemeket, amelyben szigetelök is találhatók. Az ilyen áramköri elemek természetesen a kondenzátorok, melyeknek fegyverzetei között dielektrikumok találhatók. Ilyen meggondolás alapján nevezhetjük az ilyen áramköröket "nyílt" áramköröknek is.

c.) Ellentmondások

1. Biot-Savart-törvény ellentmondás

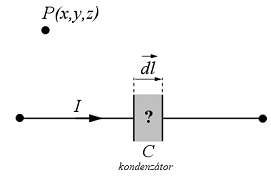
1.3 ábra

Tekintsük a 1.3 ábrát, amelyen egy zárt áramkörböl kiragadtunk egy áramköri szakasz, melyben egy permittivitású dielektrikummal kitöltött kapacitású kondenzátor található és (idöben természetesen változó) erösségü áram folyik át. Amennyiben az (1.5) összefüggéseket akarjuk alkalmazni a mágneses tér számítására, feltevödik a kérdés, hogy a kondenzátor fegyverzetei között lévö térrész, ahol nem folyik az vezetési áram, hozzájárul-e a mágneses tér értékéhez a tér különbözö pontjaiban? A képlet szerint az áramkörnek azon elemi szakaszai adnak hozzájárulást a mágneses térhez, ahol áram folyik. Ha kimérjük egy adott konfigurációjú áramkör közelében lévö pontban a mágneses tér indukcióját és kiszámítjuk azt az (1.5) összefüggéssel nem kapjuk ugyanazt az eredményt. Bízzunk a méréseink pontosságában és keressük meg az elméletben lévö ellentmondást feloldó megoldást!

2. Ampère-törvény ellentmondás

Tekintsük ugyanazt az áramköri részt, mint az elöbbi esetben. A mágneses térerösség meghatározásához az (1.7) összefüggést alkalmazzuk. Választunk a vezetö körül egy zárt görbét, majd különbözö felületeket tekintünk, melyeket a görbe kifeszít. Egyszerüség kedvéért legyen a görbe egy kör, így a különbözö felületek nem mások, mint gömbhéjak (1.4 ábra) (úgy képzelhetjük el ezeket a felületeket, mint egy szappanbuborék felületét, melyet egyre nagyobbra fújunk, de még nem vált el a kör alakú alapjától). Ábránkon az felület maga a kör felülete, az és pedig a fent említett felületek.

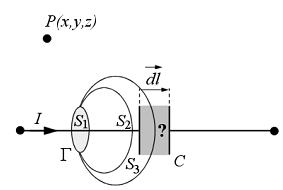
1.4 ábra

Az (1.7) összefüggés érvényes kell legyen mindhárom felületre. Az vonalintegrál minden esetben meghatározott értékü, hiszen ott nem játszanak szerepet a felületek. Viszont a jobb oldalon található felületi integrál értéke nem egyértelmü, hiszen az és felületeken áthalad a vezetési áram, viszont az felület az dielektrikumon keresztül megy át az áramköri ágon, tehát ott nem folyik a vezetési áram, ami a jobboldalon nulla értéket eredményez. Tehát ismét ellentmondáshoz vezet.

3. Ellentmondás

Ez az ellentmondás ugyancsak az Ampère-törvényhez kapcsolódik, mégpedig annak differenciális alakjához.

Mivel mindkét oldalon vektoriális mennyiségek találhatók, képezhetjük ennek az egyenlöségnek a divergenciáját. A baloldalon így egy vektortér rotációjával képezett vektortér divergenciáját számítjuk ki, amely függetlenül az eredeti vektortértöl, mindig nulla (egy vektortér rotációjából származó vektortér mindig forrásmentes!). A baloldalon viszont a vezetési áram áramsürüségének divergenciáját kapjuk, amely viszont nullától különbözö abban az esetben, amikor az áramkörben kondenzátor is találhat (nyitott áramkör). Feltehetjük a kérdést, hogy miért? A válasz az, hogy az áramsürüség erövonalai pozitív töltéseken erednek és negatív töltéseken érnek véget, ezek a töltések pedig a kondenzátor fegyverzetein találhatók. Zárt áramkör esetében mindig az áramsürüség erövonalai önmagukba záródó görbék. Matematikailag a fentieket az (1.9) összefüggés szemlélteti:

d.) Az ellentmondások feloldása. Az eltolási áramsürüség

Az ellentmondások fenti tárgyalásánál kitünt, hogy az egyetlen probléma az, hogy a "nyílt" áramkörben az áramsürüség erövonalak nem zártak. Egészen pontosan az áramsürüség erövonalak az kondenzátorok fegyverzetein lévö szabad töltéshordozókon indulnak és végzödnek tehát . Tulajdonképpen ez sugallja is a követendö utat amivel az ellentmondásokat fel lehetne oldani, nevezetesen, valahogy el kell érni, hogy az áramsürüség erövonalai "zárttá" váljanak. Hogy ezt hogyan érhetjük el egy példán keresztül szemléltetjük, majd általánosabb megfogalmazását is megadjuk.

A példa legyen egy síkkondenzátor esete. Tekintsük az 1.5 ábrát.

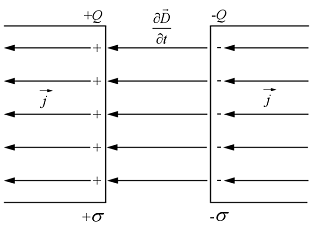
1.5 ábra

Tudjuk azt, hogy a kondenzátor fegyverzetei között lévö dielektrikumban nem mozoghatnak töltéshordozók. Töltéshordozó mozgás csak a kondenzátort a többi fémes anyagból készült áramköri elemekben és az öket összekötö vezetökben lehetséges. Tekintsük a technikai áramiránynak megfelelö pozitív töltéshordozó elmozdulási irányát. Ez a kondenzátor fegyverzeteiben és azokon kívül azt jelenti, hogy a pozitív töltéshordozók a pozitív fegyverzetet az 1.5 ábrának megfelelö irányban hagyják el, amely megadja az áramsürüség erövonalainak irányítását is. Azonban, ha áram folyik a vezetökben, a fegyverzeteken a töltéshordozók száma csökken, tehát az áramsürüség erövonalainak száma is lecsökken. Ez történik a kondenzátoron kívül. Nézzük meg a továbbiakban, mi történik a kondenzátor fegyverzetei között. Mivel a kondenzátor fegyverzetein idöben csökken a töltéshordozók száma (implicit a töltéshordozó koncentráció), a szigetelöben ezzel arányosan csökken az elektromos térerösség (implicit az elektromos indukció) is. A kondenzátorban kialakuló elektromos térerösség összefüggéssel számítható ki, vagyis az elektromos indukció a összefüggéssel. Ezen utóbbi összefüggéssel viszont kapcsolatot lehet teremteni a két jelenség között. Deriváljuk idö szerint az utóbbi összefüggést: . Az összefüggés jobb oldalán lévö mennyiségnek adjuk meg a fizikai értelmezését: ez nem már, mint az egységnyi felületen egységnyi idö alatt áthaladó töltések számát adja meg, tehát nem más, mint egy áramsürüség. Az erövonalak száma ugyanaz, mint a vezetési áramsürüség vonalainak száma, hiszen ez utóbbinak változása váltja ki a térerösség változását. Ezt az áramsürüséget eltolási áramsürüségnek nevezzük. Ez természetesen vektoriális mennyiség, melynek irányítása megegyezik a vezetési áramsürüség irányításával. Történelmileg azért kapta az eltolási áramsürüség nevet, mert úgy tekinthetö, mintha ezzel a vezetési áramsürüség erövonalainak végzödési pontjait eltoltuk volna az indulási pontjaikba. Ebböl következik, hogy ha formálisan hozzáadjuk a vezetési áramsürüséghez az eltolási áramsürüséget, az elöbbieket zárttá tesszük, tehát a mennyiség divergenciája nulla, . Ennek megfelelöen kiegészítve az (1.7) összefüggést megkapjuk az (1.1) összefüggést, mely nem más, mint az I. Maxwell-egyenlet.

Ennek az egyenletnek természetesen van mély fizikai értelme. A jobboldal elsö tagjával már megismerkedtünk, azt jelenti, hogy az árammal átjárt vezetö környezetében örvénylö mágneses tér alakul ki. Az (1.10) egyenlet második tagja viszont szintén áramsürüség dimenziójú mennyiség, s az elöbbihez hasonlóan ugyanolyan fizikai értelme van, vagyis az eltolási áramsürüség (1.tulajdonképpen az elektromos tér változása) szintén örvénylö mágneses teret hoz létre.

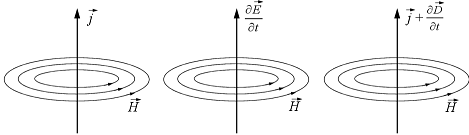
1.6 ábra

Természetesen az eltolási áramsürüség alkalmazása feloldja a másik két ellentmondást is.

1.1.2. A II. Maxwell-egyenlet

A II. Maxwell-egyenletet a Faraday-indukciótörvényböl kapjuk. Az elektromágneses indukcióról szóló IV. fejezetben tárgyaljuk a Faraday-indukciótörvényt, mely kimondja, hogy bármely tetszöleges alakú vezetö által körülfogott, mágneses indukció fluxus idöbeli változása a vezetöben elektromotoros feszültséget (e.m.f) indukál. Az indukált e.m.f.-et az (1.11) összefüggéssel adhatjuk meg. A 1.7.a ábra egy nyitott vezetö a 1.7.b ábra pedig egy zárt vezetöt ábrázol.

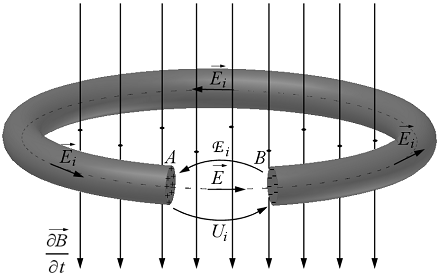
1.7.a ábra

A 1.7.a ábra alapján az e.m.f.-re és az indukált feszültségre igazak a következö kijelentések: nagyságuk egyenlö, melyet az (1.12) összefüggések igazolnak, de mérésirányuk ellentétes, melyet a 1.7.a ábra szemléltet és az (1.13) összefüggés tartalmaz:

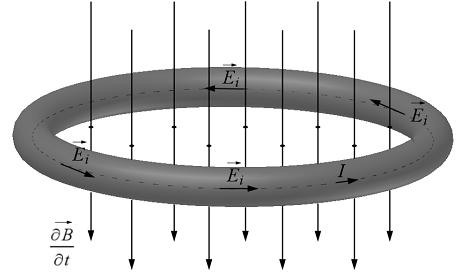
1.7.b ábra

Amennyiben a vezetö zárt, úgy abban Ohm-törvényének megfelelö áram folyik. Természetesen a Faraday-indukciótörvény most is érvényes. Áttérünk a mérhetö, makroszkopikus mennyiségekröl a nem mérhetö lokális mennyiségekre, vagyis felírjuk az indukciótörvény differenciális alakját. Definíció szerint, felírjuk az indukált e.m.f.-et, mint az idegen (töltésszétválasztó) erö zárt görbe mentén vett vonalintegrálját, és a mágneses fluxust, mint a mágneses indukciónak a zárt görbe által kifeszített felületen vett felületi integrálját:

Helyettesítsük be ezeket az összefüggéseket az indukciótörvény (1.11) alakjába:

tehát,

melyböl elhagyhatjuk az indexet és kapjuk és kapjuk az (1.2) összefüggéssel már megadott II. Maxwell-egyenlet.

Adjuk meg a továbbiakban az egyenlet fizikai értelmezését. Alakját tekintve hasonlít az (1.10) egyenlettel adott I. Maxwell-egyenlethez, tehát fizikai értelmezése is hasonló kell legyen: az idöben változó mágneses tér örvénylö elektromos teret gerjeszt. A negatív elöjel azt jelenti, hogy a mennyiségek irányításait a balmenetü fúrószabállyal adhatjuk meg (1.8 ábra).

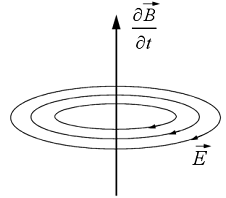
1.8 ábra

Fontos megjegyezzük, hogy eltéröen az elektrosztatikus tér és a stacionárius elektromos áram elektromos terétöl, a mágneses tér idöbeli változása által gerjesztett elektromos tér, ahogy azt az (1.17) összefüggés mutatja, nem konzervatív, viszont forrásmentes mivel az erövonalai önmagukba záródnak.

1.1.3. III. Maxwell-egyenlet

A III. Maxwell-egyenlet nem más, mint az elektrosztatikában már megismert Gauss-törvény, amely megadja az elektromos térerösség vektorának zárt felületre vonatkoztatott fluxusát, mint:

Ezt az egyenletet lehet úgy is bevezetni, hogy képezzük a gerjesztési törvény (1.10) alakjának divergenciáját.

melynek jobb oldalán tulajdonképpen kontinuitási egyenlet divergenciája található. Viszont a kontinuitási egyenlet (lásd a tárgyalását 1.1.4. pont), tehát a töltéssürüség nem más, mint az eltolási áramsürüség divergenciája.

1.1.4. IV. Maxwell-egyenlet

A IV. Maxwell-egyenlet nem más, mint a magnetosztatikában már megismert mágneses tér indukció fluxusára vonatkozik. Mivel a természetben nem létezik az elektromos töltéshez hasonló mágneses "töltés", monopólus, a mágneses indukció fluxusa egy zárt felületre vonatkozóan nem lehet zérótól különbözö. Ez azt is jelenti, hogy a mágneses tér erövonalai nem erednek és záródnak sehol sem, hanem önmagukba záródnak.

Matematikailag ugyanehhez az eredményhez jutunk, ha képezzük az (1.17) összefüggés divergenciáját (1.22):

1.1.5. A Maxwell-egyenletek teljes rendszere

Ahhoz, hogy az elektromos, mágneses és optikai jelenségeket egységesen tárgyalhassuk (ami tulajdonképpen a Maxwell-egyenletrendszer fö eredménye) ki kell egészítenünk a már megismert négy egyenletet az ún. anyagegyenletekkel. Ezeket az anyagegyenleteket is már megismertük eddig, most csak össze kell foglalnunk öket, hogy a Maxwell-egyenletrendszer teljes legyen.

Itt az anyagegyenletek legáltalánosabb alakját írtuk fel! Az anyag jelenlétének befolyását az egyenletek tekintetében egy késöbbi fejezetben tárgyaljuk.

1.1.6. A Maxwell-egyenletek alakja Descartes-koordinátákban

A Maxwell-egyenletekben vektoriális mennyiségekre ható differenciáloperátok találhatók. Ez a differenciáloperátor a Nabla operátor (), és attól függöen, hogy miként hat a vektoriális mennyiségekre, az egyenletek skaláris formában egy illetve három egyenlettel helyettesíthetök. Az alábbiakban megadjuk az egyenletrendszerben szereplö egyenletek skaláris alakjait a Descartes-i koordinátarendszerben (természetesen az egyenletek megadhatok, más koordinátarendszerekben is, attól függöen, hogy a jelenségek leírása milyen speciális koordinátarendszerben elönyösebb, ilyen a hengeres-, gömbi-, poláris koordinátarendszer stb.)

1.2. A Maxwell-egyenletrendszer anyag jelenlétében

1.2.1. A Maxwell-egyenletrendszer általános alakja

Az eddigiekben a Maxwell-egyenletrendszer vákuum esetére írtuk fel. Természetesen nagyon sok esetben kell elektromágneses jelenségeket tárgyalnunk ahol valamilyen anyag is jelen van. Ezekben természetesen már nem érvényes az Maxwell-egyenletrendszer a már megismert alakban, így ki kell egészítenünk azt. A vákuumra vonatkozó egyenletrendszerbe (1.22), helyettesítsük be a megfelelö anyagegyenleteket az (1.1)-es és (1.3)-as Maxwell-egyenletbe és végezzük el a számításokat és hasonlítsuk össze a vákuumra vonatkozó egyenletrendszerrel:

A két egyenletrendszert megfigyelve azt vehetjük észre, hogy az elektromos és a mágneses terek anyag jelenlétében ugyanúgy számíthatók ki, mint vákuum jelenlétében, csak a mágneses tér esetében a vezetési áramsürüséghez hozzá kell adni a és a áramsürüségeket, az elektromos tér esetében pedig a töltéssürüségböl ki kell vonjuk a töltéssürüséget.

1.2.2. Az anyag befolyásának szemléletes értelmezése

Adjuk meg az 1.2.1. fejezetben megjelenö mennyiségek fizikai értelmezését. Hogyan vezet a polarizáció vektorának divergenciája térbeli töltéssürüséghez? Ez abban az esetben lehetséges, ha az anyag (dielektrikum) inhomogén, tehát térfogatának különbözö részeinek más-és más a polarizálhatósága ().

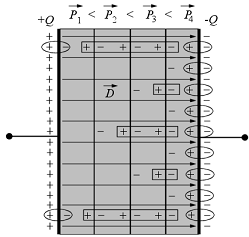
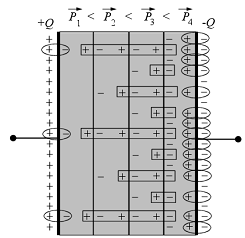
a) b)

1.9 ábra

Tekintsünk az egyszerüség kedvéért egy síkkondenzátort, amely ki van töltve egy olyan szigetelöanyaggal, melynek polarizálhatósága a fegyverzetekre meröleges irányban lineárisan változik. Gondolatban feloszthatjuk a szigetelöt olyan térrészekre, amelyeken belül a polarizálhatóság állandó, és tekintsük, hogy a polarizálhatóság balról-jobbra nö (9.a ábra). Látható az ábrán, hogy a polarizálhatóság csökkenésének az a következménye, hogy a dielektrikum térfogatában olyan polarizációs töltések is vannak, amelyek a dipólus láncok végén vannak, így nincs semlegesítö párjuk. E töltéseknek a száma megegyezik a dielektrikum felületén megjelenö erdö felületi polarizációs töltéssel, elöjele viszont ellentétes ezzel.

Ha a polarizálhatóság a fentiek mellett idöben változó, akkor idöben változóvá válik a dielektrikum térfogati polarizációs töltések száma és megjelenési helyük is. Tekintsünk egy példát az érthetöség kedvéért. Tekintsük, hogy a kondenzátor egy olyan áramkörnek a része, ahol szinuszosan váltakozó áram folyik az áramkörben. Ez azt jelenti, hogy a kondenzátor fegyverzetein a feszültség is és a dielektrikumban a térerösség is periodikusan változik. Ez viszont maga után vonja a polarizálhatóság idöbeli periodikus változását is. Míg a térerösség nö, a 9b. ábra szeleteiben is nö a polarizáció, így növekszik az elválasztó felületeken is a polarizációs töltések száma (azonban a 9.b ábrának megfelelö arányban, hiszen a polarizáció helyfüggése megmarad), mikor pedig csökken a térerösség, akkor ez utóbbi is csökken. Ez egymást követö pillanatokban úgy képzelhetjük el a térfogati polarizációs töltések megjelenését, illetve eltünését, mintha azok elmozdulnának az egyik vagy a másik a fegyverzet irányába. Természetesen elmozdulásról szó sem lehet, hiszen ezek kötött töltések, viszont a számbeli változást tekinthetjük úgy. Ennek megfelelöen definiálhatunk egy áramsürüséget, (, (1.25) összefüggés 1. egyenlet), amely hozzájárul a mágneses tér kialakításához is.

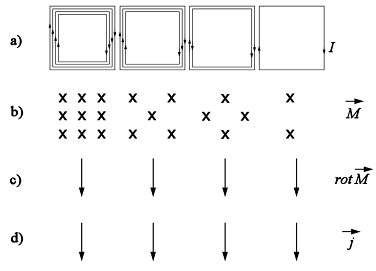
1.10 ábra

Az (1.25) összefüggés 1. egyenletében szereplö megjelenésének magyarázatához tekintsünk egy olyan tekercsrendszert, melyeknek egymás melletti tekercsei egyel kevesebb menetet tartalmaznak és ugyanaz az áram járja át öket (10.a ábra). Mágnességtanból ismerjük, hogy a egy körpályán mozgó elektron mágneses nyomatékkal rendelkezi, mely mágneses nyomaték meröleges az körpálya síkjára és megadható, mint . Ennek megfelelöen, minden az 10a.ábrán szemléltetett tekercsnek a tekercsek meneteinek síkjára meröleges mágneses nyomatékkal rendelkezik. Az egymás mellett lévö tekercsek balról-jobbra haladva egyre kisebb mágneses nyomatékkal rendelkezik, amely azt jelenti, hogy mindegyiknek párhuzamos a mágneses nyomatéka, viszont egyre ritkábbak az erövonalak (10.b ábra). Az ilyen erövonal-szerkezetü erötér rotációjával származtatott vektortér homogén és a meröleges az eredeti, mágneses nyomaték erövonal-rendszerére 10.c ábra). Elosztva ezt a mágneses permeabilitással megkapjuk az (1.25) összefüggésben szereplö áramsürüséget (10.d ábra).

1.3. A térjellemzök viselkedése különbözö anyagállandójú térrészek elválasztó felületén

Az eddigiekben tárgyaltuk az elektromágneses tér vektorait vákuumban és anyag jelenlétében. Természetesen (az optikához hasonlóan) több különbözö tulajdonsággal rendelkezö közeg alkothatja azt a térrészt, ahol az elektromágneses teret kell vizsgáljuk, így nagyon fontos az is, hogy az elektromágneses tér vektorai miként viselkednek a különbözö anyagi minöségü térrészek elválasztó felületein.

Mivel jelen jegyzetnek a tárgykörét meghaladja az elektromágneses térnek azon általános tárgyalása, amely az elektromágneses hullámokat is magába foglalja, csupán lassú idöbeli változásokat tekintünk, így elhanyagoljuk az eltolási áramot és (nem vesszük figyelembe az I. Maxwell-egyenletben a mágnesezö hatását). A jelenségek tárgyalásához a Maxwell-egyenletek képezik a kiindulási alapot.

Tekintsünk két különbözö elektromos és mágneses jellemzökkel rendelkezö homogén, izotrop közeget, ( illetve ), melyeket a felület választ el (1.11 ábra).

a) Mágneses indukció: a mágneses indukció viselkedését a legegyszerübben a IV. Maxwell-egyenlet segítségével tárgyalhatjuk. Tekintsük ennek integrális alakját (1.26), és számítsuk ki a mágneses tér indukciójának fluxusát a 11.ábrán feltüntetett henger felületére.

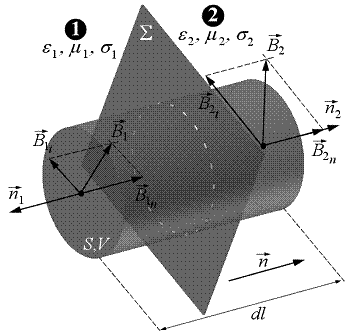
1.11 ábra

Ahhoz, hogy a matematikai számításokat elvégezhessük, tekintsünk az elválasztó felület helyett egy dl vastagságú elválasztó réteget, majd a réteg vastagságát tartassuk nulla felé, hogy kapjuk vissza a valóságos elválasztó felületet. Mivel a henger alapjai párhuzamosak az elválasztó felülettel, a mágneses indukció tangenciális (párhuzamos) komponenseinek fluxusa nulla, tehát csak a meröleges (normális) komponensek adnak járulékot a fluxushoz. Ezen kívül természetesen a tangenciális komponensek hozzájárulás adnak a fluxushoz a henger palástján, azonban ezt nem kell kiszámoljuk, mivel a réteg vastagságát nullához tartatjuk s így ez határértékben szintén nullához fog tartani. Ezt a fluxus hozzájárulást jelöljük -vel. A fluxus számításánál minden esetben a felületi meröleges a zárt felületböl kifele mutat tehát az (1.26) összefüggés a következöképpen írható át:

Az (1.28) összefüggés kifejezi, hogy a mágneses indukció vektorának normális komponense folytonosan (változás nélkül) megy át a két közeg határfelületén.

b) Elektromos indukció: az elektromos indukció viselkedését az a) ponthoz hasonlóan tudjuk tárgyalni, kiindulási pontként a III. Maxwell-egyenletet használva (1.29). A 1.12 ábra szemlélteti a számításokhoz szükséges információkat.

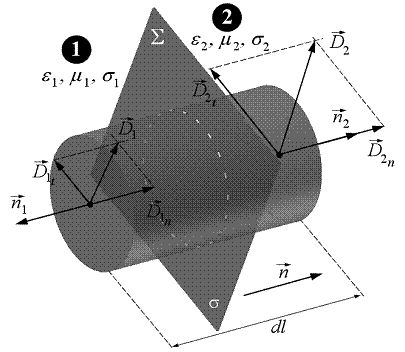
1.12 ábra

Az elözö ponthoz hasonlóan az elektromos indukció normális komponensei adnak hozzájárulást a fluxushoz, míg a tangenciálisak csakis a henger palástján, viszont ezt sem kell kiszámolnunk mivel itt is a dl vastagságot nullához tartatjuk, megszüntetve tulajdonképpen a palástot, így ez nullához tart (jelöljük -vel). Az összefüggés jobb oldala megadj az S felület által határolt V térfogatban lévö töltések számát.

Az (1.30) összefüggés jobb oldala egy olyan mennyiség, melynek dimenziója tehát ez nem más, mint felületi töltéssürüség. Jelöljük a felületi töltéssürüséget -val (), tehát,

Az (1.31) egyenlet azt jelenti, hogy az elektromos indukció vektorának az elválasztó felületére meröleges komponense ugrást szenved abban az esetben, amikor az elválasztó felületen töltések helyezkednek el és folytonosan abban az esetben, amikor a felületen nincsenek töltések.

c) Mágneses térerösség: a mágneses térerösség viselkedésének tanulmányozásához az I. Maxwell-egyenletet használhatjuk (1.32) és csak az elválasztási felülettel párhuzamos komponens viselkedését kell meghatározzuk, mivel az a) pontban már megvizsgáltunk miként viselkedik a mágneses indukció vektorának normális komponense.

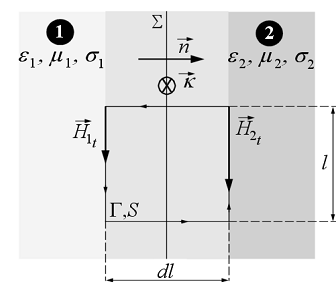
1.13 ábra

A számításokhoz a 1.13 ábrán látható zárt () görbére számítjuk ki a mágneses térerösség vektorának rotációját. A paralelogrammának az elválasztó síkkal párhuzamos oldalhosszúságán belül tekintjük, hogy a mágneses térerösség mindkét térrészben állandó. A dl átmeneti rétegben nem kell kiszámoljuk a konkrét értéket, hiszen azt ennek vastagságát a továbbiakba tartatjuk nullához, tehát ez nem ad hozzájárulást.

A mennyiség dimenziójú, melyet felületi áramsürüségnek nevezünk és ez az áram a két közeget elválasztó felületen folyik. Nem szabad elfeledkeznünk arról a tényröl, hogy az áramsürüség vektoriális mennyiség, így az (1.33) összefüggés csak a moduluszokra érvényes. Ezt át kell alakítanunk vektoriális összefüggéssé. A 1.13 ábra jelöléseivel és az irányvektor figyelembevételével az (1.41) összefüggés a következö vektoriális összefüggéssé alakítható:

Az (1.34) összefüggés azt jelenti, hogy a mágneses térerösség tangenciális komponense ugrásszerü változást szenved abban az esetben, amikor az elválasztó felületen áram folyik. Abban az esetben, amikor nem folyik áram az elválasztó felületen, a mágneses térerösség tangenciális komponense folytonosan megy át egyik közegböl a másikba.

d) Elektromos térerösség: az elektromos térerösség viselkedésének tanulmányozásához az II. Maxwell-egyenletet használhatjuk (1.35) és csak az elválasztási felülettel párhuzamos komponens viselkedését kell meghatározzuk, mivel a b) pontban már megvizsgáltunk miként viselkedik az elektromos indukció vektorának normális komponense.

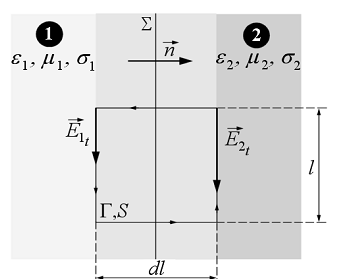
1.14 ábra

A számításokhoz a 1.14 ábrán látható zárt () görbére számítjuk ki az elektromos térerösség vektorának rotációját. A paralelogrammának az elválasztó síkkal párhuzamos oldalhosszúságán belül tekintjük, hogy az elektromos térerösség mindkét térrészben állandó. A dl átmeneti rétegben nem kell kiszámoljuk a konkrét értéket, hiszen azt ennek vastagságát a továbbiakba tartatjuk nullához, tehát ez nem ad hozzájárulást.

A mennyiség változása nem lehet végtelen nagy, így a határréteg vastagságának nullához való tartatásával az (1.36) összefüggés tart a nullához.

Az (1.37) összefüggés azt jelenti, hogy az elektromos térerösség tangenciális komponense folytonosan megy át az egyik közegböl a másikba.

1.4. Az elektromágneses tér energiája

Az elektromágneses tér energiával rendelkezik, s ez az energia idöben különbözö tényezök miatt nöhet, vagy csökkenhet. Induljunk ki a Maxwell-egyenletrendszerböl és határozzuk meg, melyek azok a tényezök, és hogyan változtatják meg az elektromágneses tér energiáját. Szorozzuk meg az (1.38) összefüggés elsö egyenletét az elektromos téreröséggel, a másodikat pedig a mágneses térerösséggel, majd a másodikból vonjuk ki az elsö egyenletet.

Az (1.39) egyenletnek a bal oldala nem más, mint az vektoriális mennyiség divergenciája (), melynek fizikai értelmezését késöbb adjuk meg. Képezzük az (1.39) egyenletnek egy zárt felület által határolt térfogaton vett integrálját.

Alkalmazzuk az (1.40) összefüggés bal oldalára a Gauss-Osztrogradszkij-integrálegyenletet, melynek segítségével áttérünk a mennyiség V térfogaton vett integráljáról a vektornak a térfogatot elhatároló zárt felületen vett fluxusának számítására és átrendezzük az egyenletet:

Vizsgáljuk meg az összefüggésben megjelenö mennyiségeket és adjuk meg a fizikai értelmezésüket. Az összefüggés bal oldala nem más, mint az elektromágneses tér energiájának idöegység alatti változása, vagyis ez egy teljesítmény dimenziójú mennyiség Az elektromos illetve mágneses terek energiasürüségét vákuum esetében az alábbi módon fejezhetjük ki (1.42):

Az (1.42) összefüggéseket helyettesítsük be az (1.27) összefüggésbe:

Az (1.41) összefüggés bal oldalán lévö elsö tagot alakítsuk át úgy, hogy a szorzatot fejezzük ki az teljes áramkörre vonatkozó differenciális Ohm-törvényböl.

Helyettesítsük be az (1.44) összefüggést az (1.43)-be és rendezzük az egyenletet:

Értelmezzük az (1.45) összefüggést. Elmondhatjuk, hogy egy adott térfogatban az elektromágneses tér energiája idöegység alatt azért csökken, mert:

a vezetökben folyó áram Joule-hö fejlödését okozza (a vezetékek melegesése okozta energiaveszteség), ezt fejezi ki az mennyiség;

ha az áram a generátoros térerösséggel megegyezö irányba folyik (az áramforrás generátor üzemmódban müködik), tehát , ami azt jelenti, hogy az elektromágneses tér energiáját növeli;

ha az áram a generátoros térerösséggel ellenkezö irányba folyik (az áramforrás fogyasztó üzemmódban müködik), tehát , ami azt jelenti, hogy az elektromágneses tér energiáját csökkenti;

mennyiség nem más, mint a V térfogatot határoló S felületen egységnyi idö alatt elektromágneses sugárzás formájában távozó energia. Az integrál alatt szereplö mennyiséget -el jelöljük és Poynting-vektornak nevezzük. A Poynting-vektor megadja az elektromágneses sugárzás saját irányára meröleges egységnyi felületen egységnyi idö alatt keresztülhaladó energiát jelenti. Mértékegysége: .

Összefoglalásként elmondhatjuk, hogy a térfogatban felhalmozott energia azért csökken, mert egy része hövé alakul, más része az idegen erök legyözésére fordítódik, ismét más része pedig a térfogatból elektromágneses sugárzás útján távozik.

1.5. Közelhatás-távolhatás

Az elektromos jelenségek tárgyalásánál az eddigiekben két különbözö szemléletmóddal ismerkedtünk meg. Az egyikkel a jelen jegyzet keretein belül csak ismétlésként találkoztunk, mégpedig az bevezetö fejezetben. Ebben a szemléletmódban a vezetökön elhelyezkedö töltések, illetve a vezetökben folyó áramok játsszák a fö szerepet és a közöttük lévö távolságtól függö módon, mintegy távolról hatnak kölcsön egymással. A kölcsönhatást a Coulomb-erövel írjuk le , melyet ennek megfelelöen távolhatási törvénynek nevezünk s ennek megfelelöen a szemléletmód a távolhatás nevet viseli. Ebben a szemléletmódban az elektromos- és mágneses terek, mint kisegítö számolási jelleggel rendelkezö mennyiségekként szerepelnek.

A jelen fejezetben tárgyalt Maxwell-egyenletek természetes egészen más, mint a Coulomb-eröé. A Maxwell-egyenletekben közvetlenül az elektromos- és mágneses terek, és nem az töltések vagy áramok vannak egymással kapcsolatban. Egy másik fontos megállapítás a Maxwell-egyenletekben szereplö mennyiségek a tér azonos pontjában azonos pillanatban vannak jelen. Ennek megfelelöen tehát elsödleges jellege a tereknek van, a töltés és az áram látszik kisegítö szerepünek, mint az elektromos tér divergenciája és a mágneses tér rotációja. Ugyanakkor az energia is kitolódik a szigetelökbe vagy vákuumba és nincs közvetlenül a töltésekhez vagy áramokhoz kötve.

Feltehetjük a kérdést, hogy melyik szemléletmód a helyes? A válasz az, hogy ameddig az idöbeli változások lassúak (nincs eltolási áram) a két szemléletmód egyenértékü, ugyanahhoz az eredményhez vezet.

Amikor azonban az eltolási áram is jelen van, amelynek mint láttuk mágnesezö hatása van, eljutunk az elektromágneses hullámokhoz. Így már végérvényesen el tudjuk dönteni, hogy melyik szemléletmód helyes. Általános esetben az elektromágneses teret semmiképpen sem tekinthetjük számolási eszközként. Tekintsünk két példát, amelyek az elözö kijelentést támasztják alá.

Pld.1. Tekintsünk egy rádió adóantennát, mely intervallunmban kisugároz egy jelet és egy vevöantennát, amely intervallumban veszi az adó által kisugározott jelet, ahol . A intervallumban, az adó már befejezte az adást, tehát az adó áramköreiben már nem folyik áram, nincsenek jelen töltések, de a vevö még nem vette a jelet, tehát a vevö áramköreiben még nem folynak áramok, nincsenek töltések. A távolhatási szemléletmód szerint az energiát a töltésekhez, áramokhoz kell kötni, de a fenti esetben az adás és a vétel között nem találhatjuk meg a kisugárzott energiát. Hol az energia? A kérdésre a távolhatási szemléletmód adja meg a választ, hiszen az energiát az adás és a vétel között minden pillanatban a megtalálhatjuk azokban a térrészekben, ahol az elektromos- és mágneses terek nullától különbözö értékkel rendelkeznek.

Pld.2. Ismert tény, hogy a csillagok "élete" is véget ér egyszer. Éltük során viszont állandó jelleggel fény bocsátanak ki, mely véges sebességgel halad a világegyetemben. Elképzelhetö tehát, hogy egy csillag, amely sok ezer fényévnyi távolságra van tölünk (1 fényév = az az út, amelyet a fény egy év alatt megtesz = 9460800000000 km) már rég megszünt létezni, még látható az égbolton, hiszen a fény amit megszünése elött kibocsátott még mindig megtalálható, az elektromos- és mágneses terekben elektromágneses energia formájában.

Megállapíthatjuk tehát, hogy az elektromágneses tér energia-felvevö, illetö szállító közeg. A relativitás értelmében a mozgó energiával impulzus is jár, tehát az elektromágneses térnek, mint energiahordozónak, illetve impulzushordozónak olyan realitása van, mint bármely részecskének.

Összefoglalásként elmondhatjuk, hogy az elektromágneses teret az elektromos töltések hozzák létre, mind a töltéseknek, mind az elektromágneses térnek reális létet tulajdonítunk, a töltéseknek azért mert diszkrét értékekben fordul elö, az elektromágneses térnek pedig azért, mert energia- és impulzushordozó.

1.6. Az elektrodinamika felosztása

Az elektromos- és mágneses jelenségeket az elektrodinamika foglalja össze, mely a Maxwell-egyenletrendszerre alapozódik. Ezen belül, a megfelelö megszorításokkal, minden jelenséget tárgyalni lehet (kivéve a Maxwell-egyenletek hiányosságaival kapcsolatos jelenségeket). Az elektrodinamika felosztását az alábbi táblázatba mutatjuk be:

1.7. A Maxwell-elmélet hiányosságai. Elektronelmélet (Lorentz-elmélet)

A Maxwell-elmélet lehetövé tette az elektromos, mágneses és optikai jelenségek egységes fenomenológiai értelmezését, s mint ilyen az egyik legjelentösebb tudományos teljesítmények közé tartozik. Azonban éppen fenomenológiai mivolta szabja meg hiányosságait, korlátait is. Mint fenomenológiai elmélet, nem veszi figyelembe a testek felépítését, korpuszkuláris jellegét. Az elmélet szerint az anyagok elektromos, mágneses és optikai viselkedése három anyagállandóval jellemezhetö ( permittivitás, permeabilitás, vezetöképesség). A Maxwell-elmélet egyik hiányossága az anyagok törésmutatójának meghatározásában rejlik. Az elmélet szerint a törésmutató és a permittivitás között érvényes az összefüggés. Ez az összefüggés csak bizonyos feltételek mellett teljesül. Ha a rezgések igen gyorsak, mint pl. a fényhullámok esetében, a törésmutató függ a frekvenciától, vagy hullámhossztól (pl. a prizma fénybontása). Ezt a jelenséget diszperziónak nevezzük, melyröl a Maxwell-elmélet nem tud számot adni. Általánosan igaz, hogy a Maxwell-elmélettel tökéletesen leírható minden vákuumban lejátszódó jelenség, viszont az anyagi közeg belsejében lejátszódó jelenségek közül azoknál, amelyeknél az anyag illetve az elektromosság korpuszkuláris szerkezetének lényeges szerepe van a jelenségek fenti három anyagállandóval történö jellemzés nem ad helyes magyarázatot (ilyen pl. az áramvezetés).

Maga a hiányosság megmutatta a követendö utat, szükségessé vált egy olyan elmélet kidolgozása, amely az anyag és az elektromosság korpuszkuláris jellegét is figyelembe veszi. Ez az elmélet a Lorentz-féle klasszikus elektronelmélet (1895), amely a Maxwell-elmélet kiegészítésével jött létre. Az elmélet támaszkodik a gázkisülések és az elektrolízis eredményeire, melyek szerint az elektromos töltés diszkrét szerkezetü és létezik egy elemi elektromos töltés (elektron). Az elektronelmélet alapfeltevése: az anyagok pozitív és negatív töltésü részecskékböl állnak (ionokból és elektronokból, késöbb viszont kiderült, hogy az ionok tulajdonképpen az atommagok), melyeket úgy kell felfognunk, hogy tulajdonképpen vákuumba vannak beágyazva, és elektromágneses kölcsönhatás van közöttük (elektromágneses tér). Ez azt jelenti, hogy az elektronelmélet azt tüzi ki célul, hogy az elektromos és mágneses jelenségeket a töltések és az elektromágneses tér kölcsönhatásaira vezessen vissza.

Az elmélet a töltéseket pontszerüeknek vagy nagyon kis térfogatú gömböknek tekinti, melyeken belül a töltéssürüség nullától különbözö. Az elektromos áramot a töltések mozgása jelenti, így az áramsürüséget a összefüggéssel adhatjuk meg. A töltésektöl származó elektromos és mágneses teret és jelölje, ahol , , és között összefüggéseket minden esetben (legyen az a töltéseken kívül vagy belül) a Maxwell-egyenelteknek az az alakja adja meg, amely -ra a vákuumra vonatkozó Maxwell-egyenletrendszerbe megy át. Ennek megfelelöen az (1.1-1.4) összefüggésekben valamint helyettesítésekkel kapjuk a Lorentz-elmélet alapegyenleteit.

Megjegyzés: az és terek jelentése nem azonos az , , és terek jelentésével. Az és terek mikrofizikai jellegüek, melyek gyorsan mozgó töltésekhez kapcsolódnak, így térben és idöben is nagyon gyorsan változnak. Példának okáért ezeket mérömüszerek segítségével nem lehet kimutatni. A fenti (1.46) összefüggésekhez járul még a töltött részecskére elektromágneses térben ható eröt kifejezö összefüggés (1.47),

melynek egységnyi térfogatra vonatkoztatott alakja a Lorentz-féle erösürüség kifejezését adja meg.